第 45 届国际大学生程序设计竞赛（ICPC）亚洲区域赛（南京）L Let‘s Play Curling

最新推荐文章于 2025-12-07 21:20:15 发布

原创最新推荐文章于 2025-12-07 21:20:15 发布 · 355 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #程序设计

这篇博客探讨了一种策略优化问题，类似于飞机票分配。红队和蓝队在数轴上有不同数量的石头，目标是红队通过选择特定点获取最高分数，分数由其石头与蓝队所有石头的距离决定。文章通过代码实现了一个解决方案，特别注意了区间处理和重复元素的排除，最终输出可能的最大得分。

飞机票
题意：本题的大体意思是，红队和蓝队在n+m的长度上，红队有n个石头，蓝队有m个，要求求红队尽可能的得分，得分规则是，确定一个c点，红队的某一个石头距离c的位置比蓝队的每一个石头都近，该石头可以得一分。
思路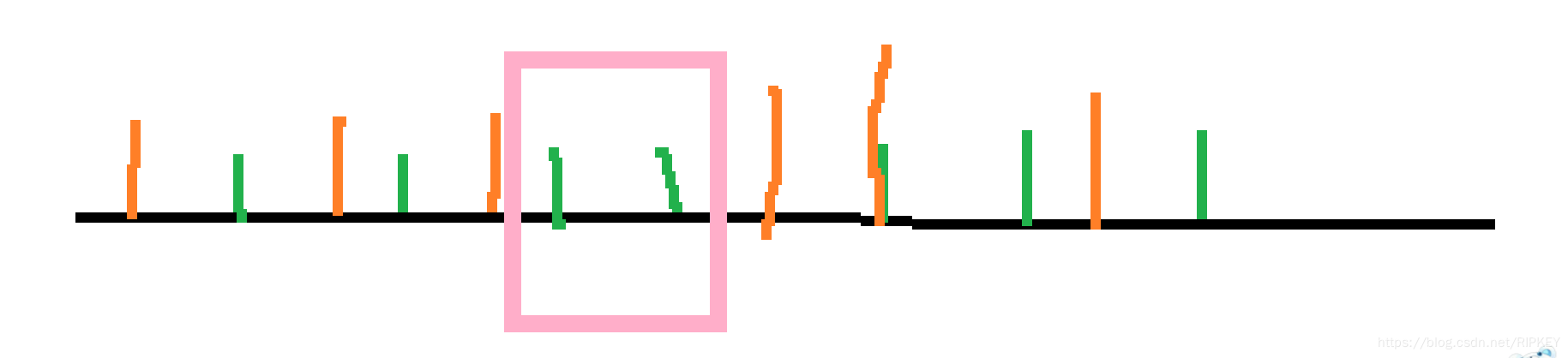：在这里插入图片描述
其实可以把题意理解为将黄色的区间内找到数量最多的绿色数。
注意两点：
①看自己的代码需不需要去重，因为如果绿色和黄色区间边块重合，那么该绿色一定不能作为答案。
②区间的边界问题，一定要注意边界，因为得提前构造一个区间，【0.无穷】这样。

const int maxn = 1e5;
int a[maxn],b[maxn],c[maxn];
int main()
{
    int n, m, t;
    cin >> t;
    while (t--) {      
        int d1 = 0, idex = 0, i, n, m;
        cin >> n >> m;
        for (i = 0; i < n; i++) {
            cin >> a[i];
        }
        map<int, int >mo;
        for (i = 0; i < m; i++) {
            cin >> b[i];
            mo[b[i]]++;
        }
        for (i = 0; i < n; i++) {
            if (mo[a[i]] == 0)
                c[idex++] = a[i];
        }
        b[m] = 0;
        b[m + 1] = 0x3f3f3f3f + 1000;
        sort(b, b + m + 2);
        sort(c, c + idex);
        d1 = unique(b, b + m + 2) - b;
        int cnt = 0, ans = 0, l = 0, r = idex - 1;
        if (r < 0) {
            cout << "Impossible" << endl;
            continue;
        }
        for (i = 0; i < d1 - 1; i++) {
            cnt = 0;
            while (c[l] > b[i] && c[l] < b[i + 1]) {
                cnt++;
                l++;
                if (l > r) break;
            }
            ans = max(ans, cnt);
        }
        if (ans != 0)
            cout << ans << endl;
        else
            cout << "Impossible" << endl;
    }
    return 0;
}