堆------神奇的优先队列

堆的定义：

堆：一种特殊的完全二叉树。

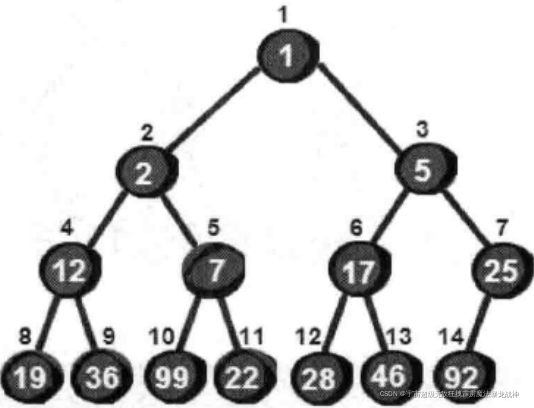
此二叉树的特点：所有父结点都比子结点要小（圆圈里面的数是值，圆圈上面的数是此结点编号）符合这样特点的完全二叉树我们称为最小堆。反之，如果所有父结点都比子结点要大，这样的完全二叉树称为最大堆。（金字塔，上面的牛逼）

最小堆的应用：

找最小值。

假如有14个数，分别是99、5、36、7、22、17、46、12、2、19、25、28、1和92，找出最小的数，最简单的方法：（时间复杂度是O（14），也就是O（N））

for(i = 1 ; i <= 14 ; i ++)
{
	if(a[i] < min)  min = a[i];
}

现在需要删除其中最小的数，并增加一个新数23，再次求这14个数中最小的一个数。只能重新所有的数，才能找到新的最小的数，这个时间复杂度也是O（N）。假如现在有14次这样的操作（删除最小的数后再添加一个新数），那么整个时间复杂度就是O（14^2）即O（N^2）。堆这个特殊的结构恰好能够很好地解决这个问题。

首先把这14个数按照最小堆的要求（就是所有父结点都比子结点要小）放入一棵完全二叉树：

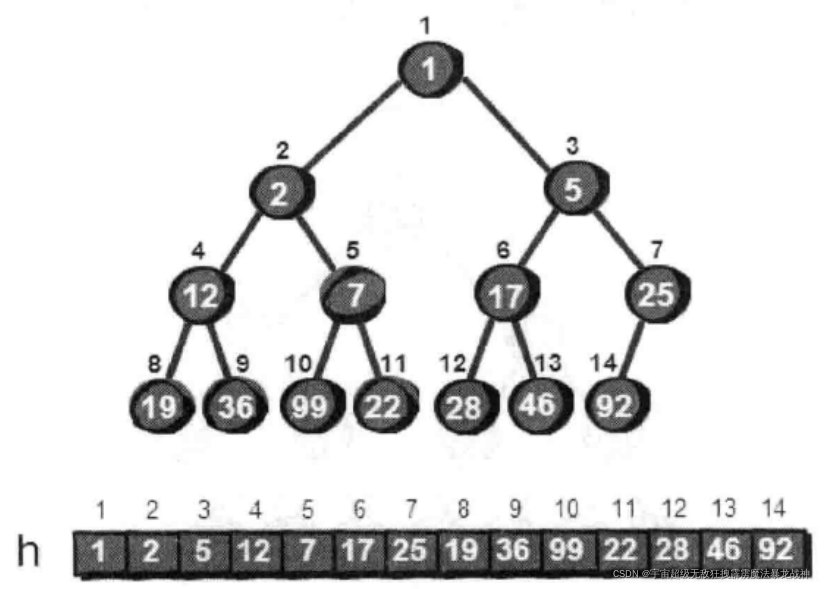
很显然最小的数就在堆顶，假设存储这个堆的数组叫做h的话，最小数就是h[1]。接下来，我们将堆顶部的数删除。将新增加的数23放到堆顶。

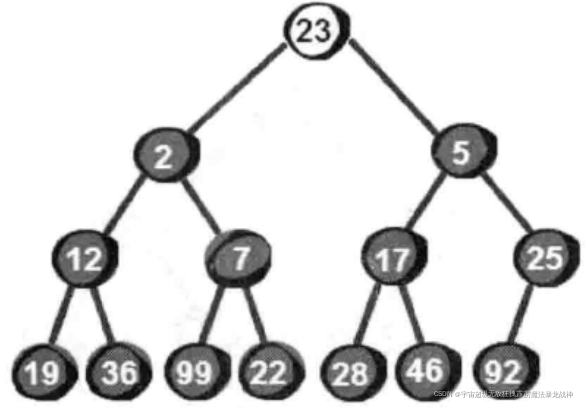
显然加了新数后已经不符合最小堆的特性，我们需要将新增加的数调整到合适的位置。那如何调整呢？

向下调整！我们需要将这个数与它的儿子2和5比较，选择较小的一个与它交换，交换之后如下。

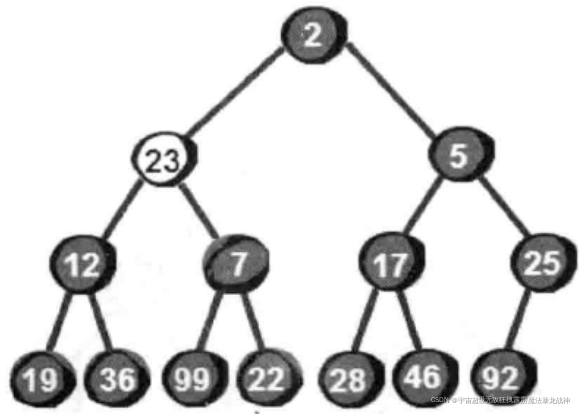
我们发现此时还是不符合最小堆的特性，因此还需要继续向下调整。于是继续将23与它的两个儿子12和7比较，选择一个交换，交换之后如下:

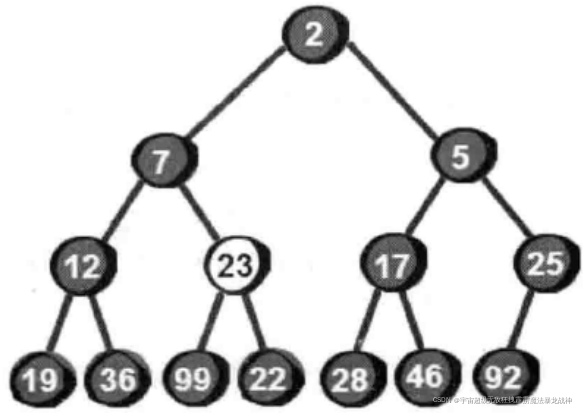
同理，继续向下调整，直到符合最小堆的特性为止。结果如下：

 

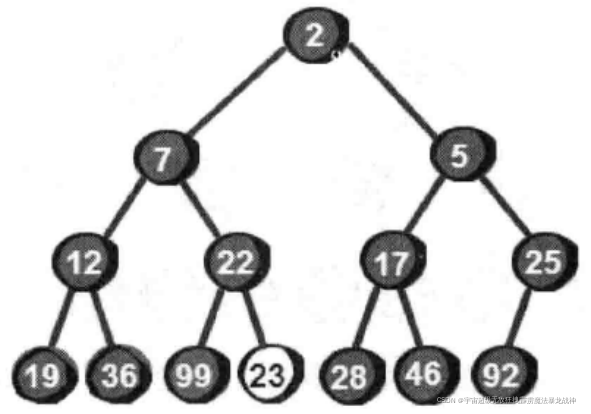
综上所述，当新增一个数被放置到堆顶时，如果此时不符合最小堆的特性，则需要将这个数向下调整，直到找到合适的位置为止，使其重新符合最小堆的特性。

调整过程如下：

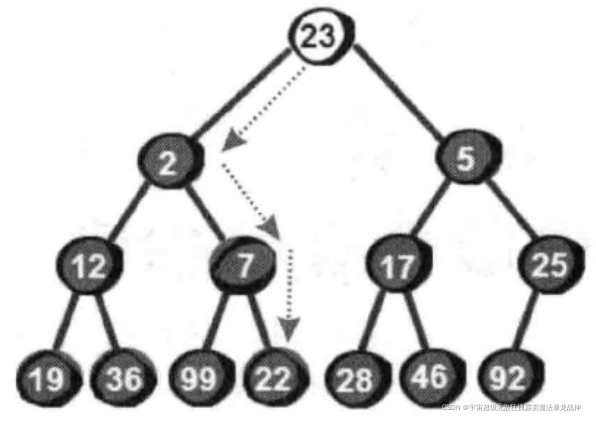
实操代码如下：

void siftdown(int i) // 传入一个需要向下调整的节点编号i，这里传入1，即从堆的顶点开始向下调整 
{
	int t,flag = 0; // flag用来标记是否需要继续向下调整
	
	//当i结点有儿子(其实是至少有左儿子的情况下)并且有需要继续调整的时候，循环就执行
	while(i * 2 <= n && flag == 0)
	{
		//首先判断它和左儿子的关系，并用t记录值较小的结点编号
		if(h[i] > h[i * 2])  t = i * 2;
		else  t = i;
		
		//如果它有右儿子，再对右儿子进行讨论
		if(i * 2 + 1 <= n)
		{
			//如果右儿子的值更小，更新较小的结点编号 
			if(h[i * 2 + 1] < h[t])  t = i * 2 + 1;
		}
		
		//如果发现最小的结点编号不是自己，说明子结点中有比父结点更小的
		if(t != i)
		{
			swap(t,i); // 交换它们
			i = t; // 更新i为刚才与它交换的儿子结点的编号，便于接下来继续向下调整 
		}
		else
		{
			flag = 1; // 否则说明当前的父结点已经比两个子结点都要小了，不需要再进行调整了 
	    }
	} 
}

我们刚才在对23进行调整的时候，竟然只进行了3次比较，就重新恢复了最小堆的特性。现在最小的数依然在堆顶，为2。而使用之前从头到尾扫描的方法需要14次比较，现在只需要3次就够了。现在每次删除最小的数再新增一个数，并求当前最小数的时间复杂度是O（3），这恰好是O（log2   N）,简写为O（logN）。假如现在有1亿个数，进行1亿次删除最小数并新增一个数的操作，使用原来扫描的方法计算机需要运行大约1亿的平方次，而现在只需要1亿*log 1亿  次。假如计算机每秒钟可以运行10亿次，那原来的方法需要一千万秒大约115天！而现在只要2.7秒！！！

存储：

基本操作：

1、交换两个点，及其映射关系

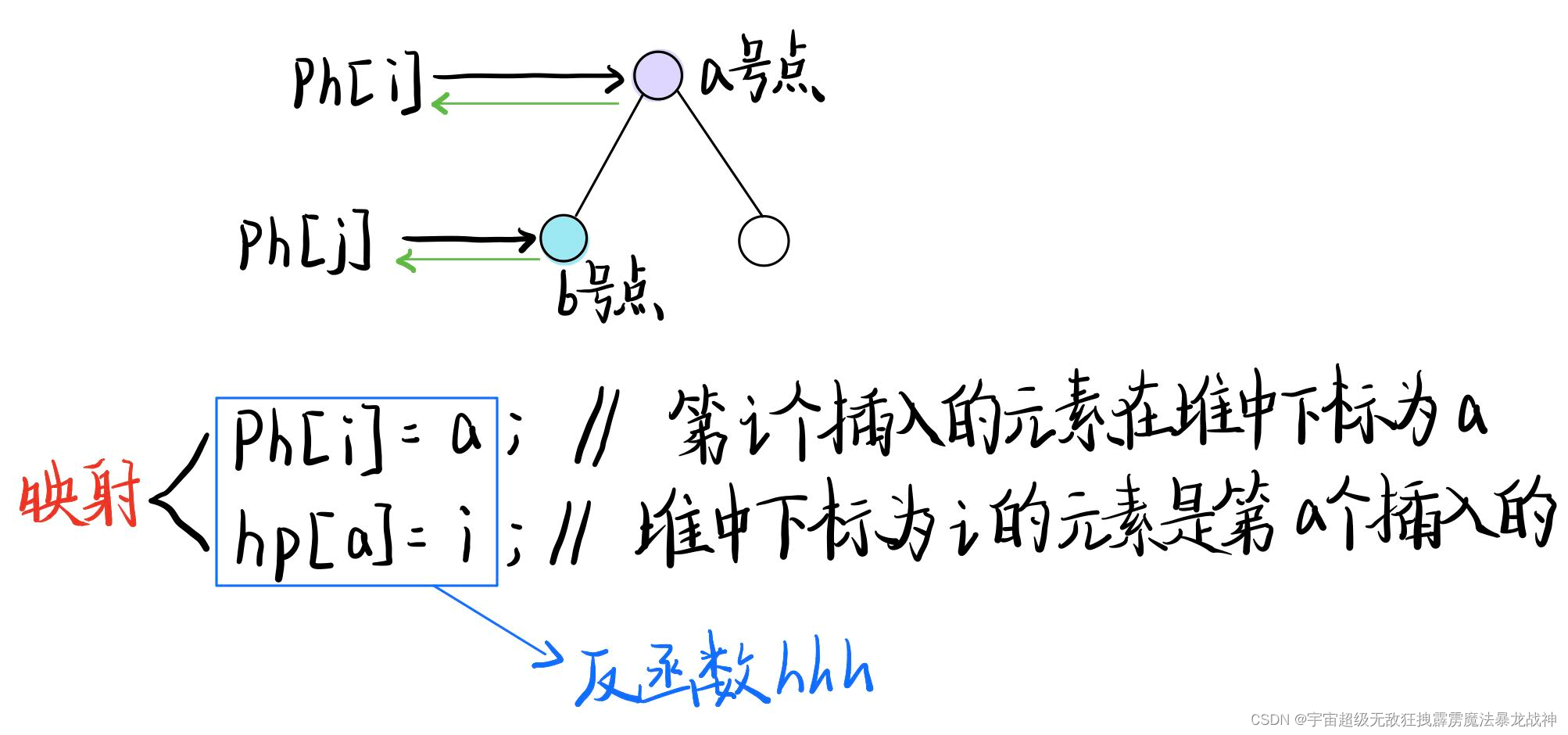
int h[N], ph[N], hp[N], size;

//交换两个点，及其映射关系
void heap_swap(int a, int b)
{
	swap(ph[hp[a]], ph[hp[b]]); // 交换ph指针
	swap(hp[a], hp[b]); // 映射关系，一一对映，交换hp指针
	swap(h[a], h[b]); // 交换堆中两个节点的值
}

2、down操作

int h[N], ph[N], hp[N], size;

//交换两个点，及其映射关系
void heap_swap(int a, int b)
{
	swap(ph[hp[a]], ph[hp[b]]); // 交换ph指针
	swap(hp[a], hp[b]); // 映射关系，一一对映，交换hp指针
	swap(h[a], h[b]); // 交换堆中两个节点的值
}

void down(int u)
{
	int t = u; // t用来存最小值 
	if(u * 2 <= size && h[u * 2] < h[u])  t = u * 2; // 左儿子存在且左儿子的值小
	if(u * 2 + 1 <= size && h[u * 2 + 1] < h[t])  t = u * 2 + 1; // 右儿子存在且右儿子的值小
	if(u != t) // 如果根节点不是最小值 
	{
		heap_swap(u,t); // 与最小值交换，使根节点称为最小值 
		down(t); // 递归下一层即继续遍历下一个结点于两个孩子的关系
	} 
}

3、up操作

up操作不用递归是因为它只需要和自己的父亲比较就可以，而down操作是父亲和自己的两个儿子比，所以需要递归处理

int h[N], ph[N], hp[N], size;

//交换两个点，及其映射关系
void heap_swap(int a, int b)
{
	swap(ph[hp[a]], ph[hp[b]]); // 交换ph指针
	swap(hp[a], hp[b]); // 映射关系，一一对映，交换hp指针
	swap(h[a], h[b]); // 交换堆中两个节点的值
}

void up(int u)
{
	while(u / 2 > 0 && h[u / 2] > h[u]) // 父结点存在且父节点大
	{
		heap_swap(u / 2,u);
		u /= 2; // 向上走一层
	} 
}

4、建堆

从n / 2层（倒数第二层）开始down，因为最后一层是叶节点，肯定满足堆的性质~

for(i = n / 2 ; i ; i--) down(i);  //n/2表示父亲的结点（比如123，3个数组成的树，3/2等于1，即表示父结点），传入的是父亲的下标

5、插入一个数

插在堆的最后，这个数相当于堆的最后一个元素，然后上移到合适位置。

代码：

heap[++ size] = x; 
up(size);

6、求集合当中的最小值

小根堆的堆顶就是最小值

代码：

heap[1];

7、删除最小值

在堆种，删尾不删头

heap[1] = h[size]; // 将最后一个元素赋给堆顶，好杀  
size --; // 删除了一个元素，堆的元素少了一个，在堆中删除最后一个元素是很简单的，如果直接删除堆顶，会破坏堆的性质 
down(1); // 将堆顶向下调整 

8、删除任意一个元素

//删除k元素
heap[k] = heap[size];
size --;
down(k); //这两个操作从形式上是都会进入函数，但是从本质上只会有一个起作用 
up(k); 

9、修改任意一个元素

//将第k个元素修改为x
heap[k] = x;
down(k);
up(k); 

10、究极模板：

//h[N]存储堆中的值,h[1]是栈顶，x的左儿子2x，右儿子是2x + 1
//ph[k]存储第k个插入的点在堆中的位置
//hp[k]存储堆中下表是k的点是第几个插入的
int h[N], ph[N], hp[N], size;

//交换两个点，及其映射关系
void heap_swap(int a, int b)
{
	swap(ph[hp[a]], ph[hp[b]]);
	swap(hp[a], hp[b]);
	swap(h[a], h[b]);
}

void down(int u)
{
	int t = u;
	if(u * 2 <= size && h[u * 2] < h[t])  t = u * 2;
	if(u * 2 + 1 <= size && h[u * 2 + 1] < h[t])  t = u * 2 + 1;
	if(u != t)
	{
		heap_swap(u,t);
		down(t);
	}
} 

void up(int u)
{
	while(u / 2 && h[u] < h[u / 2])
	{
		heap_swap(u,u / 2);
		u /= 2;
	}
}

//0(n)建堆
int i;
for(i = n / 2; i ;i --)  down(i);

题目：

题目1：（模拟堆）

维护一个集合，初始时集合为空，支持如下几种操作：

I x，插入一个数 x；

PM，输出当前集合中的最小值；

DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；

D k，删除第 k个插入的数；

C k x，修改第 k个插入的数，将其变为 x；

现在要进行 N次操作，对于所有第 2个操作，输出当前集合的最小值。

输入格式

第一行包含整数 N。

接下来 N行，每行包含一个操作指令，操作指令为 I x，PM，DM，D k 或 C k x 中的一种。

输出格式

对于每个输出指令 PM，输出一个结果，表示当前集合中的最小值。

每个结果占一行。

数据范围

1≤N≤10^5

−10^9≤x≤10^9

 

输入样例：

8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM

输出样例：

-10
6

AC代码：

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int h[N];
int ph[N]; // ph[k]存的是第k个插入的数的下标(在堆中的下标)
int hp[N]; // 存堆中的点是第几个插入的点 
int total; // heap的元素个数 

void heap_swap(int a,int b)
{
	swap(ph[hp[a]],ph[hp[b]]);
	swap(hp[a],hp[b]);
	swap(h[a],h[b]);
} 

void down(int u)
{
	int t = u; // t用来存最小值 
	if(u * 2 <= total && h[u * 2] < h[t])  t = u * 2; // 左儿子存在且左儿子的值小
	if(u * 2 + 1 <= total && h[u * 2 + 1] < h[t])  t = u * 2 + 1; // 右儿子存在且右儿子的值小
	if(u != t) // 如果根节点不是最小值 
	{
		heap_swap(u,t); // 与最小值交换，使根节点称为最小值 
		down(t); // 递归下一层; 
	} 
}

void up(int u)
{
	while(u / 2 > 0 && h[u / 2] > h[u]) // 父结点存在且父节点大
	{
		heap_swap(u / 2,u); // 交换父亲，儿子 
		u /= 2; //迭代到上一层 
	} 
}

int main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(false);
	
	int i;
	int n;
    int m = 0; // m存当前插入第几个数 
	int k,x;
	
	cin >> n;
    
	while(n --)
	{
		string s;
		cin >> s;
		if(s == "I")
		{
			cin >> x;
			m ++;
			total ++; // 堆里多加一个元素 
			ph[m] = total; // 插到堆的最后
			hp[total] = m;
			h[total] = x;
	        up(total);
		}
		if(s == "PM")
		{
			cout << h[1] << endl;
		}
		if(s == "DM")
		{
			heap_swap(1,total);
			total --;
			down(1); 
		}
		if(s == "D")
		{
			cin >> k;
			k = ph[k]; // 找到第k个插入的数在堆里面的位置
			heap_swap(k,total);
			total --;
			down(k);
			up(k); 
		}
		if(s == "C")
		{
			cin >> k >> x;
			k = ph[k];
			h[k] = x;
			down(k),up(k);
		}
	}
	return 0;
}

题目2：（堆排序）

输入一个长度为 n 的整数数列，从小到大输出前 m小的数。

输入格式

第一行包含整数 n和 m。

第二行包含 n个整数，表示整数数列。

输出格式

共一行，包含 m

个整数，表示整数数列中前 m小的数。

数据范围

1≤m≤n≤10^5，1≤数列中元素≤10^9

输入样例：

5 3
4 5 1 3 2

输出样例：

1 2 3

AC代码：

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int h[N];
int total; // heap的元素个数 

void down(int u)
{
	int t = u; // t用来存最小值 
	if(u * 2 <= total && h[u * 2] < h[u])  t = u * 2; // 左儿子存在且左儿子的值小
	if(u * 2 + 1 <= total && h[u * 2 + 1] < h[t])  t = u * 2 + 1; // 右儿子存在且右儿子的值小
	if(u != t) // 如果根节点不是最小值 
	{
		swap(h[u],h[t]); // 与最小值交换，使根节点称为最小值 
		down(t); // 递归下一层; 
	} 
}

int main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(false);
	
	int i;
    int n,m;
    
    cin >> n >> m;
    
    for(i = 1 ; i <= n ; i ++)   cin >> h[i];
    total = n;
    
    for(i = n / 2 ; i ;i--) down(i);  //n/2表示父亲的结点（比如123，3个数组成的树，3/2等于1，即表示父结点），传入的是父亲的下标
	 
	while(m --)
	{
		cout << h[1] << ' ';
		h[1] = h[total];
		total --;
		down(1);
	}
	return 0;
}