创作不易,来了的客官点点关注,收藏,订阅一键三连❤😜

前言
程序=数据结构+算法,算法是数学理论和工程实现的杂糅,是一个十分有趣神奇的学问。搞懂算法用另一种视角看编程,又会是一种全新的感受,如果你也在学习算法,不妨跟主任萌新超差一起学习,拿下算法!
系列文章目录
python每日算法 | 图文+“农村包围城市”详解堆排序,手把手学会
python每日算法 | 图文结合详解快速排序,手撕快排代码!
python每日算法 | 图文挑战十大排序算法DAY1,再也不用担心面试官问冒泡、选择、插入排序!
概述
本期的内容将介绍十大排序算法之归并排序,通过本期内容你将掌握代码归并排序如何用python实现再也不用担心面试官问归并排序是什么啦!
目录
超超python每日算法思维导图

归并排序
什么是归并排序?

归并排序(英语:Merge sort,或mergesort),是创建在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
分治法
分割:递归地把当前序列平均分割成两半。
集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
实例了解归并
| 2 | 5 | 7 | 8 | 9 | 1 | 3 | 4 | 6 |
分成了两个有序区
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
一次归并的结果
假设现在的列表分成了两段有序区,如何将其合并成一个有序序列,这个操作叫做一次归并。
已有两个有序区的代码实现
# 假设已有两个有序区的情况
def merge(lst,low,mid,high):
i = low # 左边有序区的起始标记位
j = mid + 1 # 右边有序区的起始标记位
tmp_lst = [] # 存放比较大小之后的数
while i <= mid and j <= high: # 只要左右两边有序区都有数
if lst[i] < lst[j]: # 依次判断左右两个有序区的元素大小
tmp_lst.append(lst[i])
i += 1
else:
tmp_lst.append(lst[j])
j += 1
# while执行完,肯定有一个有序区没有元素了
while i <= mid: # 左边有序区还有元素情况,则把剩下元素增加到tmp_lst
tmp_lst.append(lst[i])
i += 1
while j <= high: # 右边有序区还有元素,则把剩下元素增加到tmp_lst
tmp_lst.append(lst[j])
j += 1
lst[low:high+1] = tmp_lst # 把tmp_lst写回去,low是0,high+1因为遍历会比长度小1
lst2 = [2,4,5,7,9,1,3,6,8]
merge(lst2,0,4,8)
print(lst2)
# 输出结果
# [1, 2, 3, 4, 5, 6, 7, 8, 9]此时是已经有两个有序区的情况,那么对于无序列表如何处理呢?
归并排序算法的实现
使用归并的思路
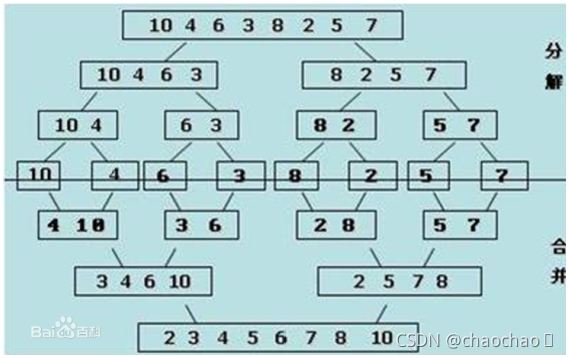
1.分解:将列表越分越小,直至分成一个元素。
2.终⽌止条件:一个元素是有序的。
3.合并:将两个有序列表归并,列表越来越大。
代码讲解
# 已有两个有序区的归并函数
def merge(lst,low,mid,high):
i = low # 左边有序区的标记位
j = mid + 1 # 右边有序区的标记位
tmp_lst = [] # 存放比较大小之后的数
while i <= mid and j <= high: # 只要左右两边有序区都有数
if lst[i] < lst[j]: # 依次判断左右两个有序区的元素大小
tmp_lst.append(lst[i])
i += 1
else:
tmp_lst.append(lst[j])
j += 1
# while执行完,肯定有一个有序区没有元素了
while i <= mid: # 左边有序区还有元素情况,则把剩下元素增加到tmp_lst
tmp_lst.append(lst[i])
i += 1
while j <= high: # 右边有序区还有元素,则把剩下元素增加到tmp_lst
tmp_lst.append(lst[j])
j += 1
lst[low:high+1] = tmp_lst # 把tmp_lst写回去,low是0,high+1因为遍历会比长度小1
# lst2 = [2,4,5,7,9,1,3,6,8]
# merge(lst2,0,4,8)
# print(lst2)
# 输出结果
# [1, 2, 3, 4, 5, 6, 7, 8, 9]
# 归并排序主函数
def merge_sort(lst,low,high): # low:下标最小的;high:下标最大的
if low < high: # 至少有两个元素
mid = (low+high)//2
merge_sort(lst,low,mid) # 递归左边化成有序区
merge_sort(lst,mid+1,high) # 递归右边化成有序区
merge(lst,low,mid,high) # 归并两个有序区
lst1 = [i for i in range(20)]
import random
random.shuffle(lst1)
print(f"初始列表:{lst1}")
merge_sort(lst1,0,len(lst1)-1)
print(lst1)
# 输出结果初始列表:
# [1, 9, 15, 18, 2, 16, 11, 0, 8, 4, 12, 13, 14, 19, 3, 10, 5, 7, 17, 6]
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]# 查看递归过程
def merge_sort_tset(lst,low,high): # low:下标最小的;high:下标最大的
if low < high: # 至少有两个元素,进行递归
mid = (low+high)//2
merge_sort_tset(lst,low,mid) # 递归左边归并成有序区
merge_sort_tset(lst,mid+1,high) # 递归右边归并成有序区
print(lst[low:high+1]) # 查看每次递归过程,输出的是每次递归的长度
# merge(lst,low,mid,high) # 归并两个有序区
lst2 = [i for i in range(10)]
import random
random.shuffle(lst2)
print(f"初始列表:{lst2}")
merge_sort_tset(lst2,0,len(lst2)-1)
print(lst2)
# 输出结果
# 初始列表:[3, 6, 7, 4, 2, 8, 0, 1, 5, 9]
# [3, 6]
# [3, 6, 7]
# [4, 2]
# [3, 6, 7, 4, 2]
# [8, 0]
# [8, 0, 1]
# [5, 9]
# [8, 0, 1, 5, 9]
# [3, 6, 7, 4, 2, 8, 0, 1, 5, 9]
# [3, 6, 7, 4, 2, 8, 0, 1, 5, 9]归并排序的时间复杂度
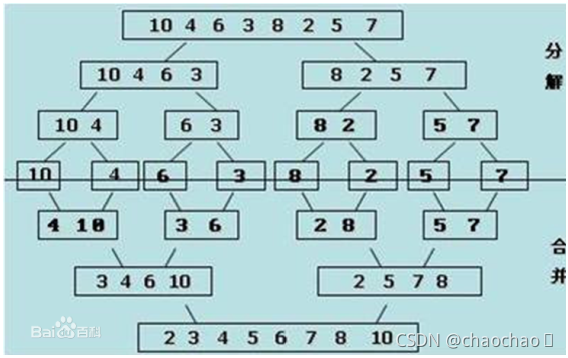
每一层遍历n个元素,总共logn层,因此得到时间复杂度为O(nlogn)
归并排序的空间复杂度为O(n),归并排序不是原地排序,创建的新的空间。
Tips:python的sort()方法是基于归并排序算法,使用的是基于归并排序timsort算法。
排序进阶三人组总结
1.时间复杂度:快速排序、堆排序、归并排序的时间复杂度都是O(nlogn)
2.一般情况下,就运行时间而言(从快到慢):快速排序(快于)归并排序(快于)堆排序
3.三种算法的缺点
①快速排序:极端情况下排序效率极低
②堆排序:在快的排序算法中相对较慢
③归并排序:需要额外的内存开销,空间复杂度大
十大排序算法之六大排序总结
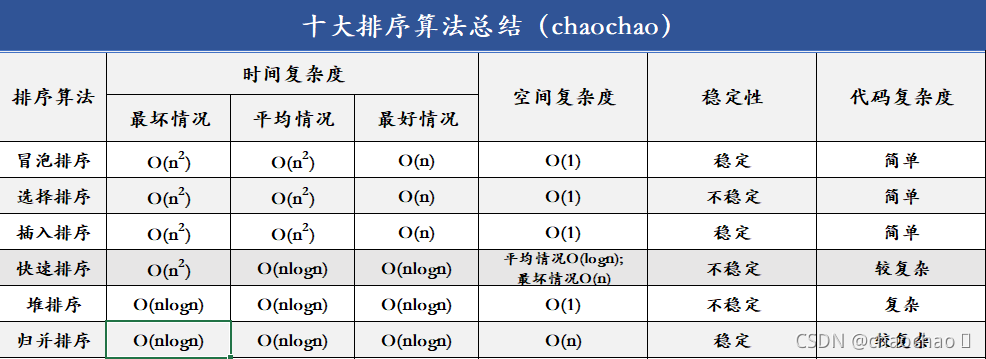
稳定性说明:
3 2 1 2 4
稳定的排序可以保证左右两边的2的位置不变;
当我们换成字典来看时:
{"name":'a',"age":18}
{"name":'b',"age":19}
{"name":'a',"age":20}
如果按字母排序,稳定的排序,两个‘a’的位置不会改变
总的来说,挨个移动比较的排序算法为稳定的排序。
代码的复杂度:代表代码难不难写,应个人能力和主观感受而定。
创作不易,客官点个赞,评论一下吧!超超和你一起加油❤😜





 本文介绍了归并排序算法,详细解释了分治法原理,并通过实例展示了如何用Python实现归并排序。内容包括归并排序的概念、已有序区的合并代码、算法实现过程及时间复杂度分析,帮助读者掌握归并排序,应对面试挑战。
本文介绍了归并排序算法,详细解释了分治法原理,并通过实例展示了如何用Python实现归并排序。内容包括归并排序的概念、已有序区的合并代码、算法实现过程及时间复杂度分析,帮助读者掌握归并排序,应对面试挑战。

















 1309
1309

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










