55.一和零

一、题目描述

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集

提示：

1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100

二、解题思路

动规五部曲：

第一步：确定dp数组（dp table）以及下标的含义

dp[i][j]:表示有i个0和j个1的strs最大子集的大小为dp[i][j]，也就是子集中的元素个数

第二步：确定递推公式

dp[i][j]可以由前⼀个strs⾥的字符串推导出来，strs⾥的字符串有zeroNum个0，oneNum个1。

dp[i][j]就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我们在遍历的过程中，取dp[i][j]的最⼤值。

所以递推公式：dp[i][j] = Math.max(dp[i][j], dp[i-zeroNum][j-oneNum] + 1)

回忆一下01背包问题中的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

对⽐⼀下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数

相当于物品的价值（value[i]）。

第三步：dp数组如何初始化

正常初始化为0就行，本题中dp[i][j]中的i和j表示的是0和1的个数，好像都不用初始化。

第四步：确定遍历顺序

01背包问题中定是外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！

本题中，strs中的字符串就是物品，背包容量就是题目中描述的m和n。

代码演示：

//第一层循环，先遍历物品
for(String str : strs){
    //统计strs数组中的0和1的个数
    int oneNum=0,  zeroNum=0;
    //遍历每一个字符串str,先将其转换成字符数组
    char[] charArray = str.toCharArray();
    for(char c : charArray){
        if(c=='0'){
            zeroNum++;
        }else{
            oneNum++;
        } 
    }
    //第二层循环遍历背包容量
    for(int i=m; i>=zeroNum; i--){
        for(int j=n; j>=oneNum; j--){
            dp[i][j] = Math.max(dp[i][j], dp[i-zeroNum][j-oneNum]+1);
        }
    }  
}

第五步：举例推导dp数组

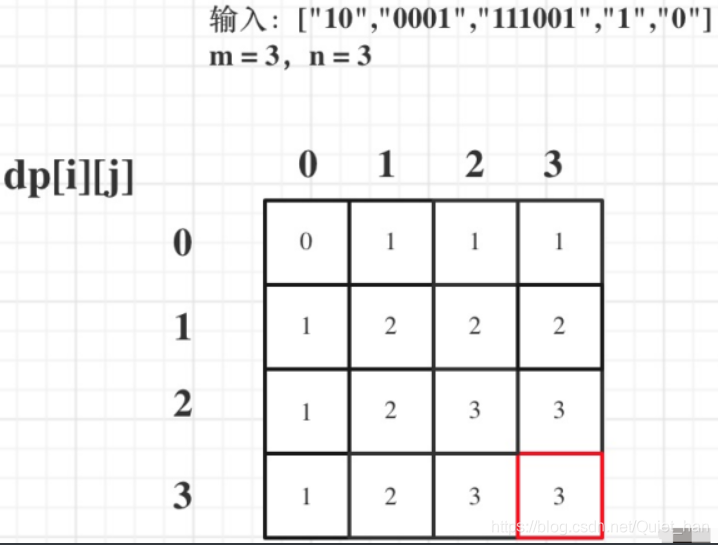
以输⼊：[“10”,“0001”,“111001”,“1”,“0”]，m = 3，n = 3为例

最后dp数组的状态如下所示：

三、代码演示

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][] dp = new int[m+1][n+1];

        //第一层循环，先遍历物品
        for(String str : strs){
            //统计strs数组中的0和1的个数
            int oneNum=0,  zeroNum=0;
            //遍历每一个字符串str,先将其转换成字符数组
            char[] charArray = str.toCharArray();
            for(char c : charArray){
                if(c=='0'){
                    zeroNum++;
                }else{
                    oneNum++;
                } 
            }
            //第二层循环遍历背包容量
            for(int i=m; i>=zeroNum; i--){
                for(int j=n; j>=oneNum; j--){
                    dp[i][j] = Math.max(dp[i][j], dp[i-zeroNum][j-oneNum]+1);
                }
            }  
        }
        return dp[m][n];
    }
}