28.山脉数组的峰顶索引

一、题目描述

符合下列属性的数组 arr 称为 山脉数组 ：
arr.length >= 3
存在 i（0 < i < arr.length - 1）使得：
arr[0] < arr[1] < … arr[i-1] < arr[i]
arr[i] > arr[i+1] > … > arr[arr.length - 1]

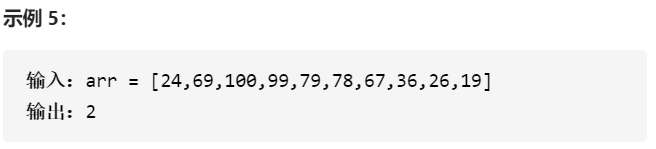
给你由整数组成的山脉数组 arr ，返回任何满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。

二、解题思路

  注意题目中的核心条件，arr[i-1] < arr[i] > arr[i+1]，在给出的数组中必定存在一个数它比它前面和后面的数都大，而且在这个数的前面是升序排列，在这个数的后面是降序排列。可以想到我们要找的数必定是数组中的最大值，我们找最大值就行。这是一种思路，另一种就是使用二分查找法。

三、代码演示

代码演示一

求数组最大值：

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int max = arr[0]; //先指定数组中第一个数就是最大值
        int index = 0; //最大值索引
        //遍历整个数组
        for(int i=0; i<arr.length; i++){
            //如果当前最大值小于arr[i]
            if(max<arr[i]){
                //将arr[i]赋给max
                max = arr[i];
                //得到此时最大值的索引
                index = i;
            }
        }
        return index; //最后们需要的也是最大值索引

代码演示二

利用二分查找法：

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int n = arr.length;
        int left = 1, right = n-2, ans =0;
        while(left<=right){
            int middle = (left+right)/2;
            if(arr[middle]>arr[middle+1]){
                ans = middle;
                right = middle -1;
            }else{
                left = middle+1;
            }
        }
        return ans;
    }
}

第4行：这里left和right的父赋值描述一下，根据题目中的描述，最大值不可能出现在数组的第一个位置也不可能出现在最后一个位置，所以left不能从0开始，right也不能从n-1开始。

第7行：判断中间这个值是不是大于它后面这个值，如果是，将middle赋值给ans，ans是用来存储最终答案的；那此时下一轮的搜索肯定不是在middle之后了，因为middle比它后面的值大，那么下一个搜索区间应该是在[left，middle-1]。

第11行：如果第7行条件不成立，那么arr[middle]<=arr[middle+1]，那么下一轮搜索空间则是在[middle+1，right]

果第7行条件不成立，那么arr[middle]<=arr[middle+1]，那么下一轮搜索空间则是在[middle+1，right]