北大华为联队夺冠：形式化数学竞赛33支队伍角逐，国产大模型啃下形式化证明硬骨头

Lean说的都队 投稿 
量子位 | 公众号 QbitAI

当大语言模型在数学推理中频频出现“幻觉”，如何让AI的数学证明像人类数学家一样严谨可靠？

这个困扰AI研究界多年的难题，在近日落幕的CCF“面向大模型的形式化数学竞赛”中找到了突破性答案。

一支名为“Lean说的都队”的联合队伍从33支参赛队伍中脱颖而出，以总分第一的成绩斩获冠军。这支北大华为的联合队伍，凭借华为openPangu-Ultra-MoE-718B和创新的技术架构，在形式化数学推理这一“AI硬骨头”上实现了重要突破。

权威赛事：瞄准大模型的数学“硬伤”

这项由中国计算机学会主办、蚂蚁数字科技等多家知名机构支持的竞赛，旨在解决大模型在数学推理中的核心痛点——“幻觉”和不可靠问题。作为CCF大数据与计算智能大赛（CCF BDCI）的重要组成部分，该赛事吸引了来自全球的33支顶尖团队参与。

与传统数学问答不同，竞赛要求参赛模型将自然语言描述的数学问题，直接转化为能被计算机验证的形式化证明代码（Lean/Litex），整个过程禁止使用任何自然语言解释。这相当于要求AI既要是数学家，又要是程序员，既要理解数学问题的本质，又要用严格的编程语言表达证明过程。

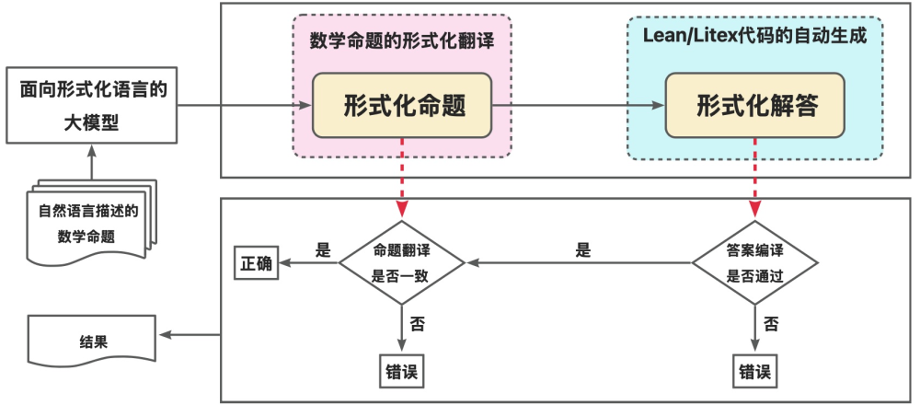
赛事组织方明确指出：“本赛题具有重要现实意义：它不仅是对当前大模型形式化推理能力的一次系统性检验，也为未来构建可信赖的大模型提供技术路径和推理能力评估基准”

硬核成绩：从33支队伍中脱颖而出

在30多支队伍，参赛人数超过600余人的激烈的竞争中，“Lean说的都队”展现出了卓越的实力。根据最终成绩统计：

初赛阶段：正确解答181道题目（共220道），初赛分数82.27分

决赛阶段：正确解答5道高难度题目（共50道），决赛分数10分

方案评审：技术方案获得87分的高分

最终总分：57.21分，位列榜首

队伍成员包括来自北京大学的袁野、刘成武、李博涛、谢佳璇、李思齐，指导教师为北京大学张铭教授。队伍在比赛中展现了强大的技术实力和创新能力。

技术突破：openPangu-Ultra-MoE-718B大模型+混合式架构

技术团队的核心创新在于构建了一个协同式求解系统，巧妙地将华为openPangu大模型的形式数学推理能力与专用证明器的高效性相结合。

openPangu大模型的卓越表现

团队采用了openPangu-Ultra-MoE-718B作为核心模型之一，这是华为基于昇腾NPU从零训练的大规模混合专家语言模型，总参数量达7180亿，激活参数量390亿，具备快慢思考融合能力。

该模型采用了业界主流的Multi-head Latent Attention（MLA）、Multi-Token Prediction（MTP）、大稀疏比等架构，以及Depth-Scaled Sandwich-Norm和TinyInit等特有设计。

在形式化数学推理任务中，openPangu大模型展现出了强大的语义理解能力和形式化表达能力，在处理抽象数学概念和复杂逻辑时表现出色。团队发现，openPangu-Ultra-MoE-718B模型在自动定理证明中最具代表性的数论和代数问题形式化任务上表现出非常强劲的性能。

在比赛的真实场景数据上的实测表明，openPangu-Ultra-MoE-718B模型在Lean的语法检查通过率方面与国际前沿的Gemini 2.5 Pro和GPT-5模型表现相当。在形式化命题的可证明性上，openPangu-Ultra-MoE-718B模型得到的命题更加适配当前的自动定理证明器，形式化命题的可证明命题比例方面更具优势。

创新的混合式架构

面对自动形式化定理证明中能力覆盖与语义对齐的双重挑战，团队提出了“能力动态分配机制”和“多层质量检查体系”。

系统架构核心特点：

1. 动态切换策略：系统首先尝试使用流水线方法，将自然语言问题输入自动形式化器生成Lean语句，经过语法和语义检查后交由专用证明器进行证明。如果流水线方法失败，系统会自动回退到单体模型方法，让前沿大语言模型直接同时完成形式化和证明任务。

2. 多层质量检查：建立了从语法正确性到语义一致性的完整质量保障体系，包括Kimina Server的语法验证和严格的语义对齐检查。

3. 多模型协同：除了openPangu大模型，团队还综合使用多种前沿模型，根据不同模型的知识边界和成本效率进行智能调度。openPangu-Ultra-MoE-718B模型因其在自动定理证明中最具代表性的数论和代数问题形式化任务上的强劲的性能而作为默认模型。

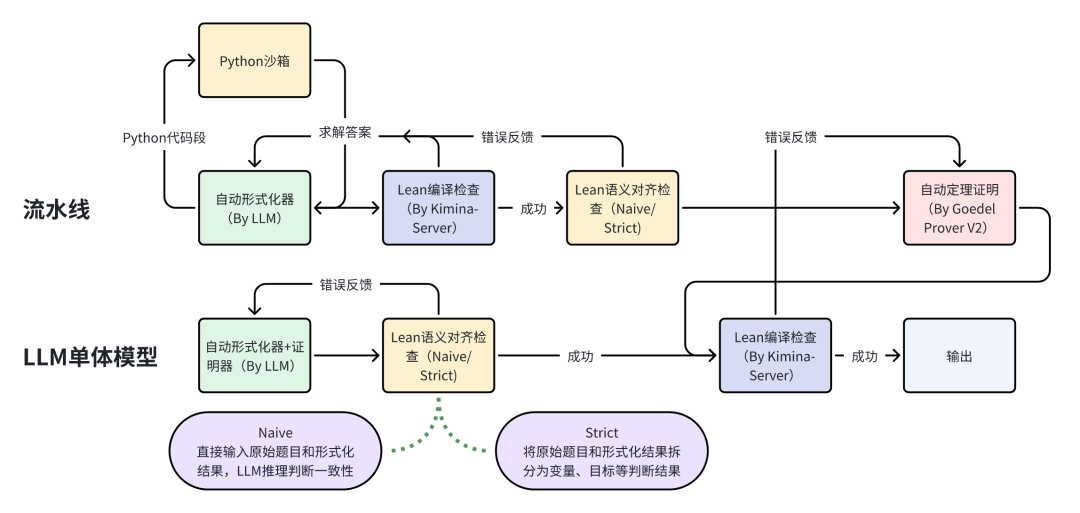
关键创新：语义分解验证机制

特别值得一提的是团队在语义对齐检查上的突破。传统方法使用LLM-as-a-Judge进行整体判断，容易出现“判定过松”问题——即形式化结果可能通过表面语义检查却与原问题存在本质偏差。

团队创新性地引入了基于语义分解的多层级验证机制，将自然语言问题解构为数据类型、前提条件和证明目标三个正交维度，实现了从整体模糊匹配到结构化精确对齐的范式转变。这一方法来自于团队的先前工作：FMC: Formalization of Natural Language Mathematical Competition Problems, ICML 2025 AI4Math Workshop。

“我们通过对在线评测反馈的深入分析，识别出传统语义对齐方法存在系统性的判定过松问题，”团队解释道，“针对这一根本性弱点，我们引入了基于语义分解的多层级验证机制，将自然语言问题解构为类型、前提和目标三个正交维度，实现了从整体模糊匹配到结构化精确对齐的范式转变。”

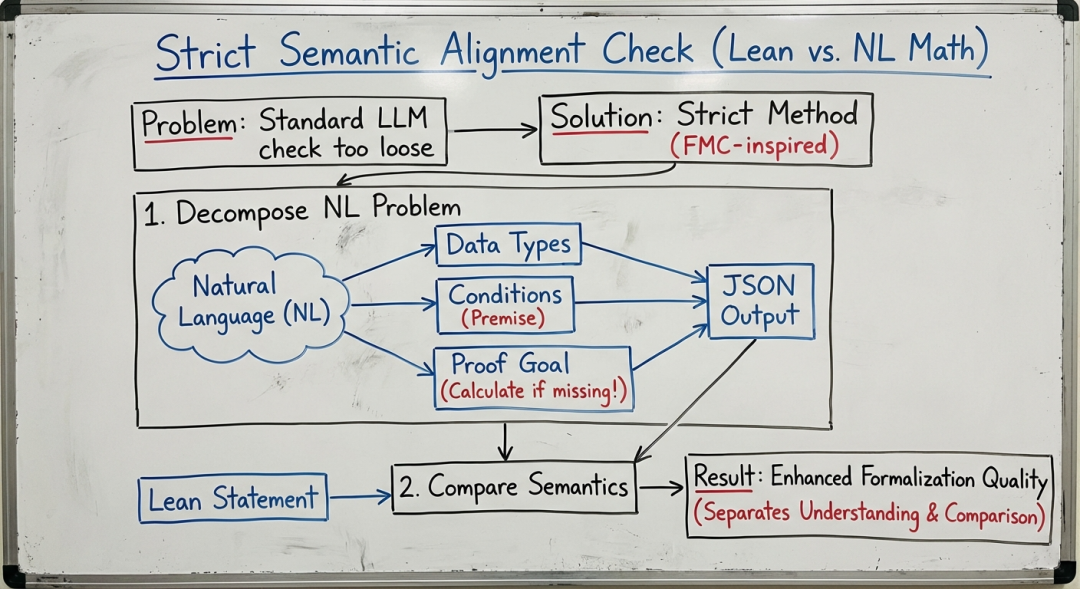
相比传统方法，这一改进显著降低了误判率，为形式化结果的可靠性提供了坚实保障。

实战案例：从抽象代数到复数计算

在实战中，这一技术架构展现出了强大的适应性。团队分享了两个典型案例：

案例一：抽象代数问题（c4078）

原始命题：“设R’/R是环的整扩张，证明rad(R)=rad(R’)∩R，其中rad(R)表示R的幂零根。”

模型表现：团队设计的流水线成功处理了这一抽象命题的推理与表达，生成了严谨的Lean代码，准确处理了环论中的核心概念。

import Mathlib.RingTheory.Nilpotentimport Mathlib.RingTheory.IntegralClosureopen Idealtheorem nilradical_eq_of_integral_extension [CommRing R] [CommRing R'] [Algebra R R']    (h : Algebra.IsIntegral R R') (hinj : Function.Injective (algebraMap R R')) :    nilradical R = (nilradical R').comap (algebraMap R R') := by  ext x  constructor  · intro hx    rw [mem_comap]    obtain ⟨n, hn⟩ := mem_nilradical.mp hx    exact mem_nilradical.mpr ⟨n, by rw [← map_pow, hn, map_zero]⟩  · intro hx    have hx' := mem_comap.mp hx    obtain ⟨n, hn⟩ := mem_nilradical.mp hx'    apply mem_nilradical.mpr    use n    apply hinj    rw [map_pow, hn, map_zero]

案例二：复数计算问题（c27）

原始命题：“有多少个实数c满足|3-ci|=7？”

模型表现：系统通过拆解子问题、计算中间结果，最终生成完整的形式化证明。模型展示了处理复数计算与拆解问题的能力，通过生成子定理并最终汇总成完整证明。