神经网络学习,又叫做神经网络的训练算法,可以通过计算和更新神经网络本身的权值和阈值,加强网络自身的学习能力。
一.神经元模型
神经网络最基本的模型就是神经元模型,也是神经网络中的简单单元。神经元常用的简单模型是M-P神经元模型,如下所示:
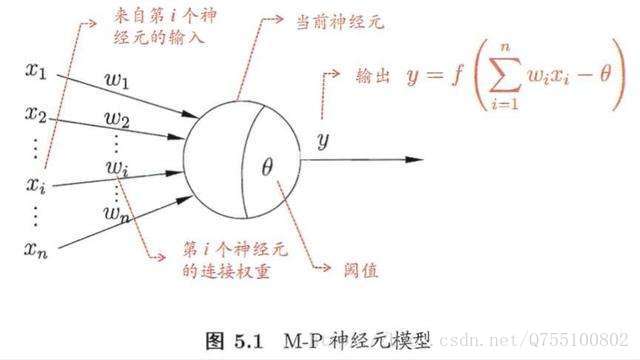
阈值:就相当于神经元的兴奋电位,当这个神经元的输入电位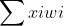 大于这个神经元的阈值时,它就会被激活,向其他神经元发送电位,所以输出
大于这个神经元的阈值时,它就会被激活,向其他神经元发送电位,所以输出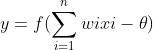 ,而函数f表示的是一个激活函数,它将函数的输出值挤压到(0,1)的范围之内,函数图像如下
,而函数f表示的是一个激活函数,它将函数的输出值挤压到(0,1)的范围之内,函数图像如下
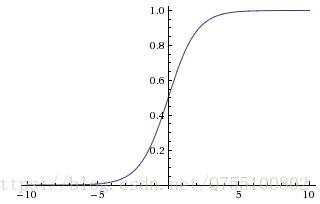
其他常用的也有符号函数什么的,不过不够光滑。
为了简化表示,通常我们把阈值 θ记为 −w0,并假想有一个附加的常量输入 x0=1,那么我们就可以把神经元的输入记为 ∑ni=0wixi 或以向量形式写为 w⋅x,把输出记为 y=f(∑ni=0wixi)。
把许多个这样的神经元按一定层次组合,就得到一个神经网络。
二.感知机
感知机由两层神经元组成,输入层接受外部信号后传给输出层,输出层就是M-P神经元,亦称“阈值逻辑单元”,由阈值的大小将输入的数据分为多种逻辑组合。感知机的激活函数 ff 就是之前介绍过的阶跃函数,因而我们可以把感知机函数写为
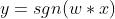
y=sgn(x)就是我们熟悉的符号函数。还可以把感知机看作是 n 维实例空间中的超平面决策面,对于超平面一侧的实例,感知器输出 1,对于另一侧的实例输出 0,这个决策超平面方程是 w⋅x=0。 那些可以被某一个超平面分割的正反样例集合称为线性可分(linearly separable)样例集合,它们就可以使用感知机表示。
所以,给定训练集,感知机的权重wi和阈值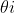 就可以通过学习得到。由上述可以阈值也可以当做一个-1w0的权值,所以学习过程就可以统一为权值的学习。学习规则非常简单,对训练样本(x,y),若当前感知机输出为
就可以通过学习得到。由上述可以阈值也可以当做一个-1w0的权值,所以学习过程就可以统一为权值的学习。学习规则非常简单,对训练样本(x,y),若当前感知机输出为 ,则调整公式如下:
,则调整公式如下:








 本文介绍了神经网络的基础,包括神经元模型、感知机和BP(误差逆传播)算法。神经元模型中,M-P神经元模型通过阈值和激活函数实现信号传递。感知机作为简单的神经网络,能解决线性问题但无法处理非线性可分问题。BP算法通过反向传播误差,更新权重和阈值,使多层前馈神经网络逼近任意复杂度的连续函数,是深度学习中的重要概念。
本文介绍了神经网络的基础,包括神经元模型、感知机和BP(误差逆传播)算法。神经元模型中,M-P神经元模型通过阈值和激活函数实现信号传递。感知机作为简单的神经网络,能解决线性问题但无法处理非线性可分问题。BP算法通过反向传播误差,更新权重和阈值,使多层前馈神经网络逼近任意复杂度的连续函数,是深度学习中的重要概念。
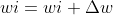
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








