损失函数的研究，二元分类和多分类（LR 和softmax）

简介

在做GBDT的时候遇到的一个坑现在把它填上。

二元分类和多分类的问题形式上看去简单，但是当我们仔细思考的时候还是有很多坑的。我再也不敢说自己精通Logistic模型了，本来以为都掌握了原理，其实并不然。

损失函数一般分为四种，平方损失函数、对数损失函数、softmax损失函数、hingeloss损失函数。平方损失函数很容易理解，一般用于回归问题。这里就不做讲解了。

逻辑回归与对数损失函数

这部分内容主要参照了https://www.cnblogs.com/ModifyRong/p/7739955.html，写的非常非常好，我这篇对数损失函数几乎是照着这个写的，对一些问题的解答加上自己的理解

一句话概括逻辑回归：逻辑回归就是假设数据服从伯努利分布，通过极大似然法，用梯度下降去求解参数，得到最大的概率，最后让数据能够二分类。

逻辑回归的基本假设有：

假设1：假设数据服从伯努利分布。伯努利分布有一个简单的例子是抛硬币，抛中为正面的概率是p,抛中为负面的概率是1−p.在逻辑回归这个模型里面是假设 hθ(x) 为样本为正的概率

假设2：样本为正的概率为

假设3：我们的目标函数是极大似然函数最大化：

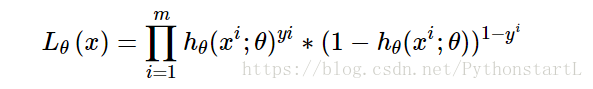
问题的转化：

我们对极大似