聊聊如何增强LLM的推理规划能力之MCTSr算法——蒙特卡罗树搜索与LLM的结合

最新推荐文章于 2025-04-27 23:46:36 发布

Python_金钱豹

最新推荐文章于 2025-04-27 23:46:36 发布

阅读量1.6k

点赞数 15

文章标签：算法语言模型人工智能自然语言处理 YOLO llama

本文链接：https://blog.youkuaiyun.com/Python_cocola/article/details/143129731

版权

概述

arxiv论文地址：Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B[1]

MCTSr：MCT Self-Refine算法；即将蒙特卡罗树搜索（MCTS）与LLM集成在一起的方法，重点是提高LLM在复杂数学推理任务中的表现。

MCTS是一种决策工具，广泛用于人工智能中需要战略规划的场景，通常用于游戏和复杂的环境解决问题。通过将MCTS的系统探索能力，与LLM的自我完善和自我评估能力相结合，创建一个更强大的框架，以解决当前LLM难以解决的复杂推理任务。

在使MCTS适应LLM集成方面存在一些技术挑战。传统的MCTS策略可能不能很好地与LLM输出的随机性和生成性相一致，LLM输出通常涉及无限的、连续的潜在动作空间。这种偏差需要在MCTS框架内定制期望计算和反向传播方法，以更好地适应llm的独特特性。

此外，我们引入了一种动态剪枝策略，该策略包含改进的上置信度界（UCB）公式，以优化高风险任务中有效决策所必需的探索新选项（以获取更多信息）-利用已知的好选项（以最大化利益）之间的平衡。

MCTS

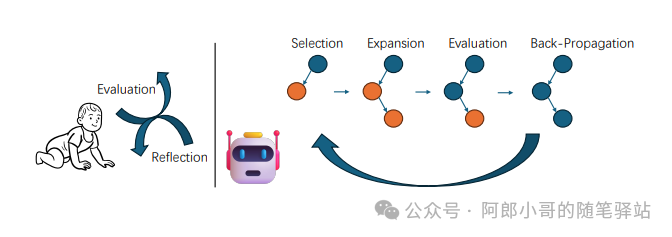
蒙特卡罗树搜索（MonteCarloTreeSearch，MCTS）是一种广泛应用于博弈和复杂决策过程的决策算法，它通过构建搜索树并模拟结果来估计/更新行动的价值。通常，MCTS算法包括四个不同的阶段：

选择：算法从根节点开始，根据特定的策略（如UCT/UCB）在有希望的子节点之间进行导航，直到到达一个叶节点。
扩展：在叶节点，除非它代表游戏的终端状态，否则将添加一个或多个可行的新子节点来说明潜在的未来移动。
模拟或评估：从新添加的节点开始，算法进行随机模拟——通常被称为"滚动"——通过任意选择移动，直到达到游戏的结论，从而评估节点的潜力。
反向传播：模拟后，结果（赢、输或平局）被传播。

通过这些阶段的反复迭代，MCTS逐步构建决策树，在由于状态空间的巨大而无法直接计算最佳策略的情况下，提炼出最优决策策略。

置信度上限（Upper Confidence Bound UCB）算法，或者说应用在树结构的上限置信区间（Upper Confidence Bound Applied to Trees UCT）算法；在MCTS的选择阶段是至关重要的，通过选择最大化的行为来平衡探索和利用：

其中为动作的平均奖励，为父节点的总访问次数，为模拟访问节点的次数，为平衡探索和利用的常数。

MCTSr（MCT Self-Refine）算法将蒙特卡罗树搜索（MonteCarloTreeSearch，MCTS）与LLM相结合，将数学问题解的迭代精炼（refine）过程抽象为搜索树结构。这棵树上的节点代表不同版本的答案，而边表示改进的尝试。该算法的操作流程遵循MCTS算法的一般模式。具体来说，我们采用自我反思驱动的自我完善来完善答案；使用模型的自我奖励能力对不同答案版本的奖励进行抽样。

为了方便理解MCTSr算法，定义了以下符号和函数：

P：正在处理的问题实例。
A：节点的集合，每个节点代表P的一个潜在答案。
M：每个节点上可用的一组操作，表示对答案可能进行的自完善修改。
R：根据修改的质量和有效性对节点的自我奖励进行抽样的函数。
Ra：存储节点a所有自奖励抽样结果的集合，具有自奖励函数R。
T：根据达到最大迭代次数或获得满意的答案质量等标准确定搜索过程终止的函数。
Q(a)：一个估计答案节点价值的值函数a，由累积奖励Ra和子节点的反向传播推导而来。
U(a)：节点a的Q值的置信度上限，以平衡开采和勘探之间的关系。
Father(a)：返回给定节点a的父节点的函数。如果a是根节点，则此函数返回null或特定标识符。
Children(a)：返回给定节点a的所有子节点集合的函数，表示通过执行操作m∈M从a派生的所有可能状态。
N(a)：节点a的总访问量，用于计算节点的UCB值，评估节点的勘探开发状况。因为我们将为每次访问取样一个奖励，所以这个值等于|Ra|。

方法论

MCTSr的主要结构如下：

详细介绍每个组件MCTSr的主要工作流程如下：

初始化：根节点是使用原始模型生成的答案和假回答（如 “我不知道”）建立根节点，以最小化模型过拟合倾向。
选择：算法采用值函数Q对所有未完全展开的答案进行排序，并采用贪心策略选择值最高的节点进行进一步的探索和细化。
Self-Refine：选择的答案a使用自精炼（refine）框架进行优化。最初，模型生成一个反馈m，指导精炼（refine）过程生成一个增强的答案。
自我评价：对精炼（refine）后的答案进行评分以获得一个奖励值，并计算其Q值。这涉及到模型自我奖励反馈和约束，如严格的评分标准和抑制满分，以确保评分的可靠性和公平性。
反向传播：将精炼（refine）答案的值向后传播到它的父节点和其他相关节点，以更新树的值信息。如果任何子节点的Q值发生变化，则更新父节点的Q。
UCT更新：在更新了所有节点的Q值之后，我们确定候选节点的集合C，以便进一步扩展或选择，然后使用UCT更新公式更新下一个选择阶段的所有节点的UCT值。

该算法遍历这些阶段，直到达到终止条件满足T，包括推出限制或最大探索深度，不断改进答案的质量，并探索新的可能性。

总览

在解答数学问题时，MCTSr中的大模型首先会像正常流程一样生成初步答案（甚至可以是“我不知道”），但并不会直接作为输出。

为了改进这个初始答案，MCTSr算法会对其进行评估和反馈，语言模型会被要求对答案进行评价和批评，分析其中可能存在的问题。

然后大模型基于反馈进行自我修正，产生一个新的答案，这个新版本会纳入搜索树中，成为一个新的子节点。

针对多个子节点，系统会进行评分和奖励采样，计算出该节点的“Q值”（a表示答案节点，Ra表示a的奖励样本集合，|Ra|表示样本数量），可以看出Q值的计算综合考虑了节点在最坏情况和平均情况下的表现。

为了提高评估的可靠性，系统采用了严格的打分标准，并会进行重复采样，同时还采取了禁止模型给出满分等策略。

然后基于Q值，MCTSr会使用改进的UCB公式计算每个叶子节点的UCT值，选择UCT值最高的节点进行扩展。

计算UCT值的目的，是为了平衡了节点的平均奖励和访问频率，避免单纯追求高Q值导致的效率下降。

此外，作者修正的UCT计算公式中还引入了动态调整探索系数c，以便在搜索过程中适应不同的问题复杂度，并在探索广度和深度之间做出平衡。

被选中的节点，会通过大模型再次进行自我修正，生成新的答案节点，然后再次进行自我评估并计算Q值。

新的Q值会被并反向传播到其父节点和祖先节点，确保了搜索树中节点的质量评估随着搜索的进行而不断改进。

根据新的Q值和访问次数，各个节点的UCT值也会被重新计算。

接着，上述步骤会被不断重复，直到满足预设的终止条件，此时具有最高Q值的答案节点被视为问题的最优解。

总的来说，通过蒙特卡洛搜索、自我完善与大模型的集合，MCTSr实现了数学问题最优解的生成。

UCB是一种实现总奖励最大化的方式，UCT是将UCB策略应用于树形搜索问题的一种算法；可以看作是差不多的东西。

Self-Refine

在self-refine的过程中，通过多轮对话精化prompt引导模型优化一个答案到问题。最初，模型生产关于的反思性或批判性评论。随后在的指导下，该模型修改以产生改进版本。这种迭代精化提高了答案的质量，利用结构化反馈来驱动答案的演变。

自我评价

在数学问题的精化问题中，答案的值被定义为进一步提炼为高级答案的预期质量，这是因为从到其重写形式的过渡具有马尔科夫性质。与传统的MCTS（估计状态中的行动值）不同，这里的来自归属于的奖励函数值的多个采样。

该模型利用自奖励（self-reward）方法来估计的奖励。其中需要提供从-100到100的奖励分数。我们发现，在没有约束的情况下，模型的奖励倾向过于平滑，导致在实践中答案之间缺乏比较区分。为了解决这个问题，设计了三个约束：

提示约束：模型在奖励评分时必须遵守最严格的标准。
满分抑制：指示模型不提供完整的反馈分数；任何超过95分的奖励都会减少一个固定的数量，以抑制过高的分数。
重复采样：对搜索树节点的每次访问都涉及对该节点的奖励进行重复采样，以增强自我评估的可能性。需要注意的是，在对一个节点的子节点进行奖励采样时，也将对其父节点进行奖励采样，以增加奖励采样的样本量。

采样后，计算的值。为抵消自奖励函数的平滑倾向，在期望奖励中加入最小值约束，进一步细化答案质量估计。

其中为答案的质量值，为的奖励样本集合，为中的最低奖励，为样本数量，为中所有奖励的总和。这个公式通过平均奖励的最小值和平均值，平衡最坏情况和平均结果来计算。

反向传播

在所有叶节点的奖励值采样和值更新完成后，将会将此更改传播到其父节点和祖先节点。在此更新过程中，如果节点的子节点集合Children(a)中的任何元素的函数值发生变化，则该节点的函数值将更新为

其中是考虑其子节点影响的答案的更新质量值，是仅考虑其奖励样本的朴素质量值，代表的子节点中最高的质量值。该公式通过对当前值及其后续子节点的最佳可能结果求平均值来改进。

更新UCT和Selection

在更新树中所有节点的值之后，我们继续进行下一轮选择的选择阶段。这个过程包括一下步骤。

候选节点选择：利用数学问题精化过程的马尔可夫性质。专注于选择所有叶节点和那些未完全扩展的叶节点，而不考虑精化路径的历史是可行的。这种路径无关性有助于简化我们的问题。在选择节点时，我们不再需要从根节点开始，而是按层次顺序遍历树中的节点。

但是，考虑到在此任务中充当策略的LLM可以为任何答案状态生成无限数量的细化操作。每个节点都可能面临一组无限的扩展操作。因此，借鉴贝叶斯优化中的期望改进概念，本文提出了两个确定"完全扩展"的标准：

节点的子节点数量达到预定义的限制。
至少有一个子节点的值超过该节点。

我们根据这些标准确定候选节点的集合，以便进一步扩展或选择。该策略有助于准确定义哪些节点可能在后续搜索中产生更高价值的答案，从而提高整体搜索效率和结果质量。

UCT更新：借鉴AlphaGo，我们使用UCT和UCB-1方法来平衡节点的探索和利用；对于候选集中的节点，其值为：

其中是答案的值，是给定节点的总访问次数，是平衡利用和探索的常数，是用于避免被零除的小常数。

排序和选择：根据候选集的UCT值，我们可以选择一个最优节点，通过贪婪采样或重要性采样来探索精炼（refine）过程。

终止函数

在MCTSr算法中，搜索终止函数准则可以从以下几个条件推导出来：

提前停止：当搜索结果的改进效果减少或连续搜索产生重复结果时，就会终止。
搜索约束：一旦展开数量达到预定限制，或当树中的一个或多个节点满足最大深度约束时，搜索将终止。
基于语言模型Logits的高级标准：搜索基于来自语言模型Logits的预定义指标进行总结。

一旦满足了终止功能条件，我们就可以根据值或是其他条件从树节点中收集最佳答案。

结论

本文论证了MCT self-refine（MCTSr）算法在提高大型语言模型（LLMs）求解复杂数学问题的能力方面的有效性。通过将蒙特卡洛树搜索（MCTS）与llm集成，MCTSr解决了准确性和可靠性方面的关键挑战，特别是在数学推理任务中。实验结果证实，在跨多个数据集解决问题的成功率显著提高，包括在奥林匹克级数学挑战中的显着表现。

此外，该研究推进了llm在复杂推理任务中的应用，并为未来AI技术的整合奠定了基础，以提高决策和推理的准确性。尽管MCMCTSr在数学问题解决方面展示了潜力，但其在更广泛背景下的适用性，如黑盒优化和自驱动对齐，仍有待探索，未来的工作将优化算法组件。

如何学习大模型 AI ？

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

在这里插入图片描述