Python数据可视化系列之幂律分布

1.幂律分布

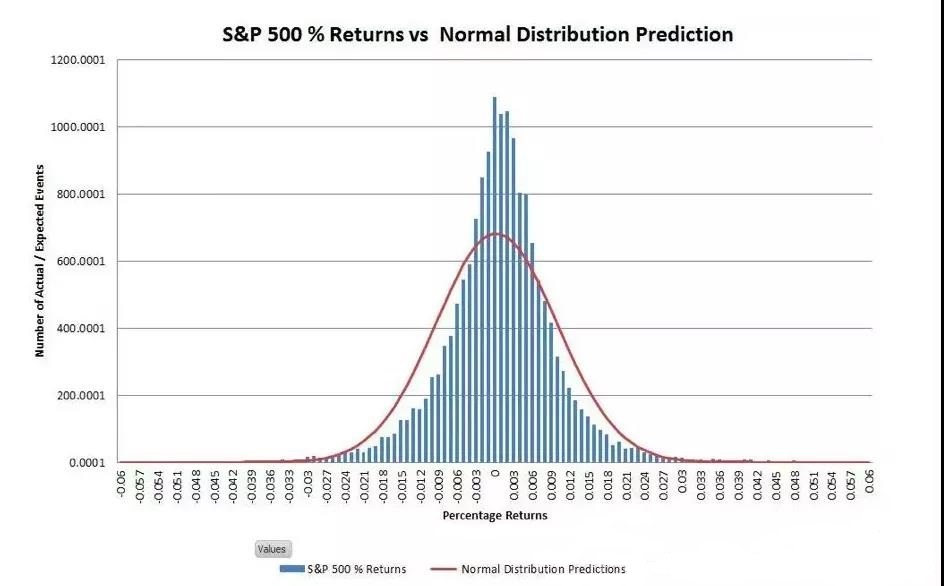
首先要说的是中心极限定理——在复杂的多因素情况下，只要个体相互独立，集体效果就应该是正态分布。然而实际运用中，尤其是金融中，更多面对的是尖峰胖尾现象，比如下面这幅图描述的是标普500指数的收益率分布，很明显的是，实际的收益率的分布和理想中的正态分布不一致，这就是所谓的尖峰胖尾特征，峰值更高，尾巴部分也拖的更长更厚。正是有了尖峰胖尾，可以想象，有些东西可以超出想象的大，并且出现这个的概率也非常大，这样的陡峭且延长很长的分布就是所谓的幂律分布（两个特征：陡峭，延长很长）。

2.公式推导

幂律分布就是概率密度函数服从幂函数的分布，对幂律分布公式：

对公式两边同时取以10为底的对数：

令：

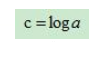
且c为常数，所以公式变成：