[ABC380E] 1D Bucket Tool 题解

题目大意

一行中有 $N$ 个单元格，编号为 $1$ 至 $N$ 。
最初，$i$ 单元格被涂上了颜色 $i$ 。
给您 $Q$ 个查询。请按顺序处理它们。每个查询属于以下两种类型之一：

1. 1 x c：将以下单元格重新涂成颜色 $c$ ：通过重复移动到与当前单元格相同颜色的相邻单元格，从单元格 $x$ 到达的所有可到达单元格。

2. 2 c：打印涂上颜色 $c$ 的单元格数量。

题目分析

第一眼看到这题目就觉得相邻单元格一起改变就可以用并查集来做。画图分析一下就可以知道第一类查询只是与 $x$ 联通的连通块给改变颜色并把相同颜色的块给连在一起组成更大的连通块。

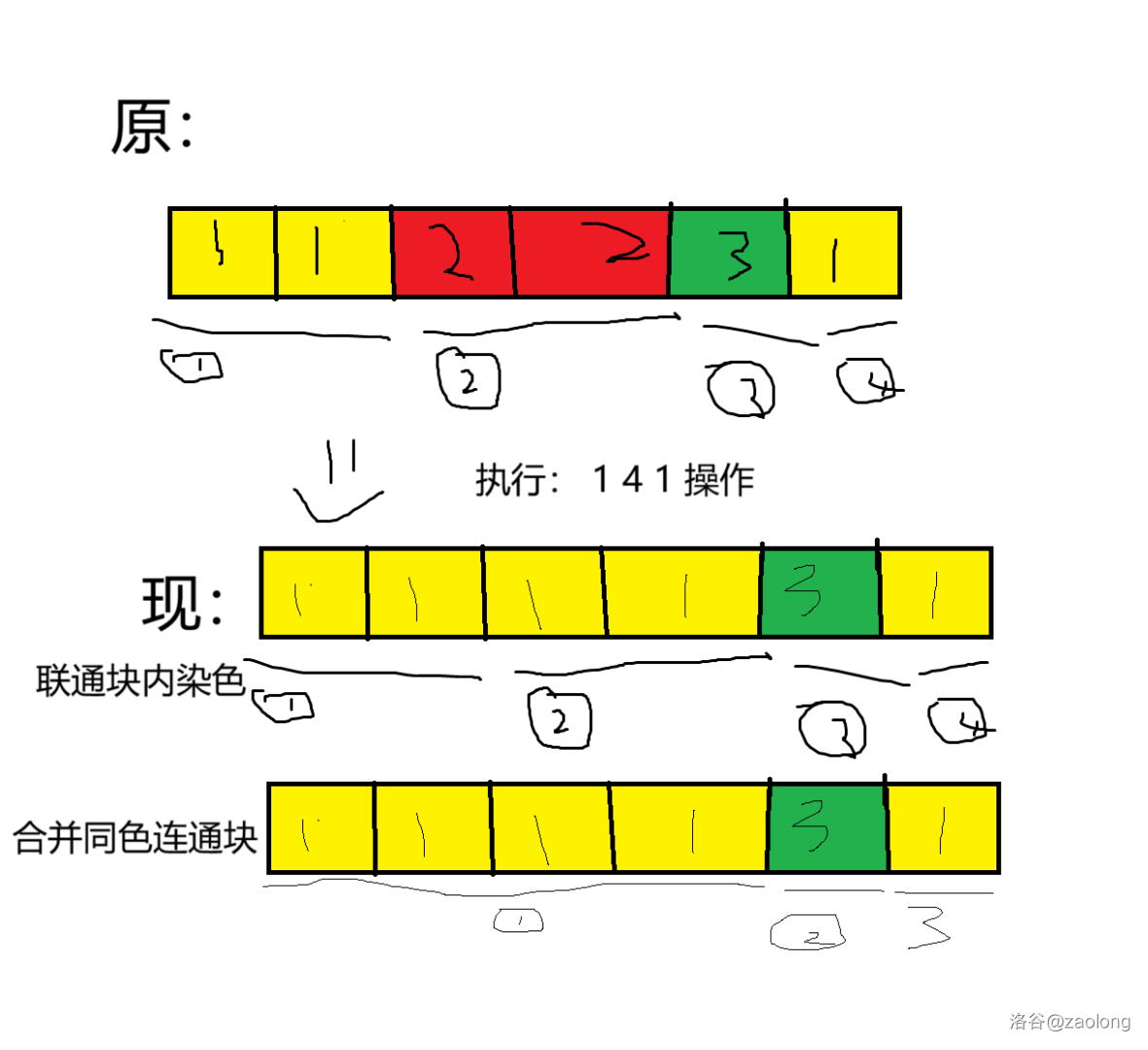
剩下详见代码注释。

代码

#include<bits/stdc++.h>
using namespace std;
//ans[i]表示颜色为i的小方块个数。 
//co[i]表示父亲为i的联通块的颜色。 
//s[i]表示父亲为i的连通块内方块的个数。  
//a[i]记录i的父亲节点。 
//l[i]和r[i]的父亲的连通块左边界与右边界。  
int n,t,ans[500005],co[500005],s[500005],a[500005],l[5000005],r[500005];
//寻找x的父亲。
int find(int x){
	if(a[x]==x) return x;
	return a[x]=find(a[x]);
}
//初始化 
void init(){
	for(int i=1;i<=n;i++){
		co[i]=a[i]=l[i]=r[i]=i;
		ans[i]=s[i]=1;
	}
}
//第一类处理 
void point(int k,int c){
	//找到k的父亲 
	int f=find(k);
	//在原来的颜色数量上减去块内方块的个数
	ans[co[f]]-=s[f];
	//在现在的颜色数量上减去块内方块的个数
	ans[c]+=s[f];
	//更改颜色 
	co[f]=c;
	//更新边界 
	l[f]=min(l[f],k);
	r[f]=max(r[f],k);
	//查看左右边界的连通块 
	int x=find(l[f]-1),y=find(r[f]+1);
	//如果颜色相同但父亲不一样 
	if(co[f]==co[x]&&f!=x){
		//连接 
		a[x]=f;
		//加上新添加的数量 
		s[f]+=s[x];
		//更新边界 
		l[f]=l[x];
	}
	//如果颜色相同但父亲不一样 
	if(co[f]==co[y]&&f!=y){
		//连接 
		a[y]=f;
		//加上新添加的数量 
		s[f]+=s[y];
		//更新边界 
		r[f]=r[y];
	}
}
void print(int c){
	//第二类查询只用输出ans[c]的之就可以了 
	cout<<ans[c]<<"\n";
}
main(){
	cin>>n>>t;
	init();
	while(t--){
		int op,k,c;
		cin>>op;
		if(op==1){
			cin>>k>>c;
			point(k,c);
		}else{
			cin>>c;
			print(c);
		}
	}
	return 0;
}