题意: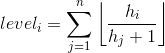
输入n,n个数 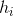 ;输出对应的
;输出对应的
思路:
hi:
{2 3 5 9}
hi+1:
{3 4 6 10}
EX:
hi+1中
(这里的贡献 即 hi/(hj+1) 如 2/3=0 3/3=1 5/3=1 9/3=3)
3对于0 1 2 的贡献为0 ;3,4,5的贡献为1;6,7。8 的贡献为2 ;9,10,11的贡献为3
仅记
3,6,9.....即对3的倍数的贡献
为了降低复杂度
将3 6 9 12 对应贡献+1
再求前缀实现+2 +3
那么此时 3对hi中3,5的贡献为1,9的贡献为3
同理
处理4对 4(4,5,6,7),8(8,9,10,11),12(12,13,14,15)...的贡献
最后可得所有(hi+1)对 hi 里面元素的总贡献值
代码:
#include<bits/stdc++.h>
using namespace std;
#define maxn 2000100
int num[maxn];
int n,a[maxn];
int Max;
int main()
{
cin>>n;
Max=0;
memset(num,0,sizeof(num));
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
Max=max(a[i]+1,Max);
}
for(int i=0;i<n;i++)
{
int k=a[i]+1;
int x=k;
while(x<=Max)
{
num[x]++;
x+=k;
}
}
for(int i=1;i<maxn;i++)
num[i]+=num[i-1];
for(int i=0;i<n;i++)
{
if(i) printf(" ");
printf("%d",num[a[i]]);
}
printf("\n");
return 0;
}





 本文解析一道算法竞赛题目,通过贡献法优化计算复杂度,详细介绍了如何利用贡献法快速求解每个元素对整体结果的贡献值,适用于处理大规模数据集。
本文解析一道算法竞赛题目,通过贡献法优化计算复杂度,详细介绍了如何利用贡献法快速求解每个元素对整体结果的贡献值,适用于处理大规模数据集。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








