算法学习（6） 数学问题求解系列（3）亲密数（开挂加速版，必看）

前言

上一篇博客介绍了亲密数的常规解法(点击传送门回顾)。这篇介绍的算法，运用了空间换时间的编程思路，极大的缩短了程序的运行时间。

加速思路

1. 求解10万以内的亲密数，也就是，从2到10万，每一个数肯定是都要求因子和，这一步省不了，依然要求
2. 上一个解法中，我们每求一个因子和后，把它当成新的数，再求一次因子和，这就相当于我们把2到10万，又求了一次因子和，也就是第一步，又执行了一遍，自然时间就很长了
3. 于是，假如我们把第1步，求得的因子和，全部储存下来（10万个存储空间，对于现代计算机是小case）；这里要注意，数字作为索引，因子和作为该位置的数存储进去，比如$10$的因子和是$1+2+5=8$，那么numList10] = 8
4. 最后问题就变成简单的比较了，程序按索引找数据，这种处理，时间短得可以忽略不计
5. （敲黑板的重点！） 最后一步也是一个循环，从数组的头开始，比如数a，我们只需要判断numList[numList[a]] 是否 等于 a， 即可~这一步很绕，好好花时间琢磨

小结

上面的加速思路，还是逃不出空间换时间的本质。在时间和空间之间平衡，或许就是编程的乐趣之一吧~现在不停写着给程序加速，这体验真的很令人着迷

实现代码

# 下面的思路是，先求出每一个数的因子和，最后在数组查找即可
def FindCloseNum2():
    MaxNum = 20000
    factorList = [0]*MaxNum  # 用来存储因子
    closeNumList = []
    for num in range(2, MaxNum):
        factorList[num] = GetSumFactor(num)  # 每个数字被用作索引，存储他们的因子和
    # 然后，接下来对factorList处理就可以了
    for i in range(2, MaxNum):
        if factorList[i] > i and factorList[i] < MaxNum:  # 排除完数及防止重复
            if factorList[factorList[i]] == i:
                closeNumList.append(i)
                closeNumList.append(factorList[i])
    # 输出完数
    count = 1  # 统计个数
    for i in range(0, len(closeNumList), 2):
        print('第', count, '对：', closeNumList[i], '和', closeNumList[i+1])
        count += 1

运行结果

这里增加了时间统计。

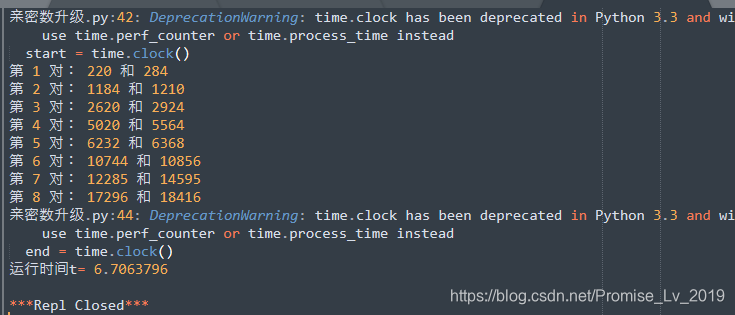
代码分析和注意点

1. 时间运行是6秒，也就是你点运行，要数6下，才会有结果，是不是很意外？！但这就是为什么我们一直追求好算法的原因
2. maxNum = 20000, factorList = [0]*MaxNum # 用来存储因子，这个数组，按一个整数16bit 来算，需要约40kBytes 的空间，看来还是很划算，因为1024k Bytes 才等于 1M Bytes
3. 下图是上一个程序的运行时间截图，同样是20000的范围。多了4秒，如果数字规模更大的话，差距会更加明显
   

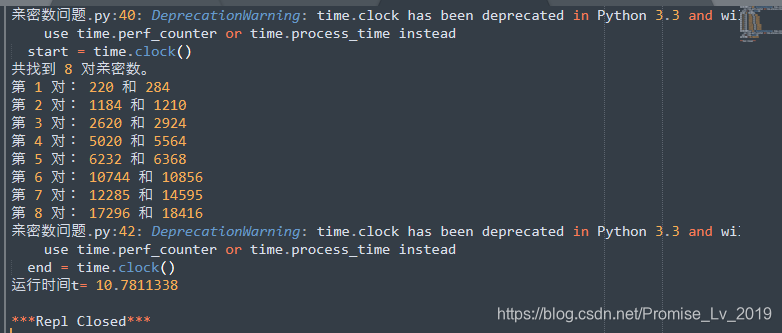
还能更快吗？

当然可以！！！指数的速度提升！！！

抱歉！上面的优化没有戳到真正的痛点……
其实，真正拖慢程序的罪魁祸首是求因子和的函数

# 先单独写一个求因子和返回因子和的函数
def GetSumFactor(num):
    factorSum = 0
    for j in range(1, num//2+1):  # 一个整数，不存在比它自身一半大的真因子
            if num % j == 0:  # 如果j是i的因子
                factorSum += j
    return factorSum

大家关注这个语句，for j in range(1, num//2+1)：，这里的复杂度是 $O(n)$, 虽然我们已经除以一半，但依然是这个复杂度。所以，随着问题规模的扩大，程序越来越慢！

于是，加速来了！

加速的求因子和代码

def GetSumFactorFaster2(num):
    factorSum = 1
    for j in range(2, int(math.sqrt(num)+1)):  # 把数组规模根号缩小
        if num % j == 0:  # 判断不要太多
            if j < num // j:
                factorSum += j + num//j  # 怎么去掉 j == num // j 的情况呢
            else:
                factorSum += j
    return factorSum

代码分析

1. 当 num % j == 0时，$j$是因子， $num/j$ 就不是了吗？所以，我们遍历到 $\sqrt{num}+1$就可以啊！你可能会说，这有什么特别的。不特别吗？ 当$num=20000$, $num/2=10000$, 而 $\sqrt{num}=141$, 遍历规模是原来的一百分之一啊！这便是计算机科学家一直追求的指数加速效果！
2. 对于比如 $16=4\times 4$， 4 只需要加一次，容易被忽略的一点

运行结果对比

（不要太惊讶）

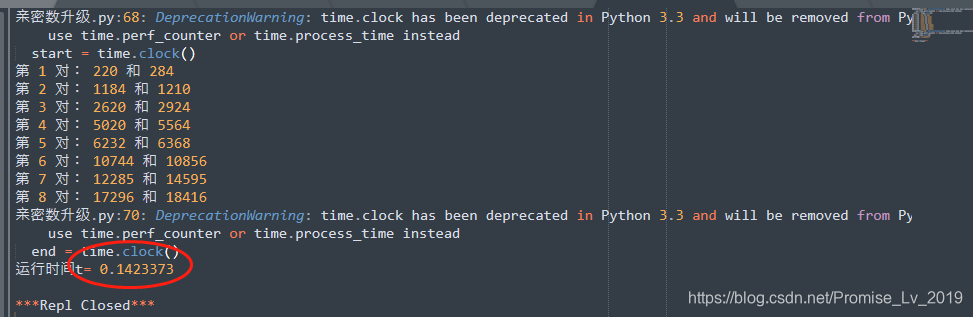
你没看错，从 $6.70s\to 0.14s$！ 这就是指数加速的魅力啊~
对于第一个程序（传送门），虽然用了两次求因子和，但是加速效果也很惊人。

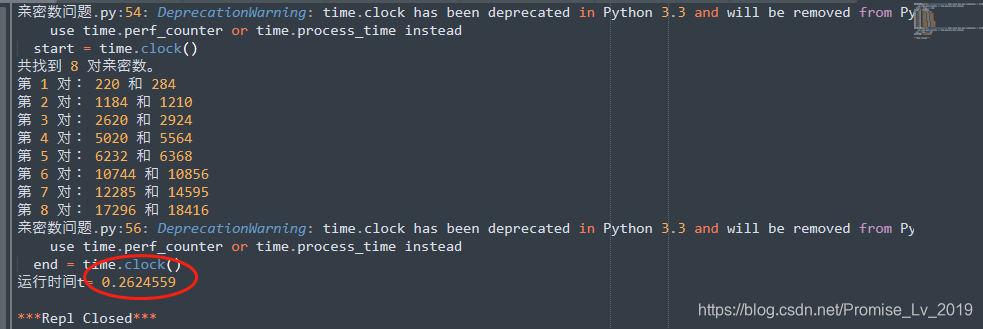
从 $10.78s\to 0.26s$！ ，也就是，求因子和才是决定整个函数运行快慢的关键！我在第一部分，用“空间换时间”的方法，起的作用是减少一次求因子和的过程，所以，速度提升，接近一次求因子和的时间。

总结

第一次这么强烈的感受到程序效率的提升，可以带来这么大的差别，随之而来的喜悦感，竟然是如此强烈~开心 ~ Keep Coding ~