Leetcode169. 多数元素

原创已于 2022-04-10 12:45:35 修改 · 481 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #分治 #随机化 #排序

于 2022-04-09 23:31:38 首次发布

Every day a LeetCode 专栏收录该内容

550 篇文章

订阅专栏

这篇博客介绍了四种不同的方法来寻找数组中的多数元素，包括使用哈希表、排序、随机化选择和Boyer-Moore投票算法。每种方法都有其独特的优势，例如哈希表提供快速查找，排序则利用了数组的特性，而Boyer-Moore投票算法则在效率上表现出色。这些算法展示了在解决同一问题时，不同思路的应用和比较。

Every day a leetcode

题目来源：169. 多数元素

解法1：hash

因为数组是非空的，并且给定的数组总是存在多数元素，所以hash表中的最大值对应的下标就是多数元素。

代码：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        unordered_map<int,int> hash;
        int ans=0;
        int cnt=0;
        for(int i:nums)
        {
            hash[i]++;
            if(hash[i]>cnt)
            {
                ans=i;
                cnt=hash[i];
            }
        }
        return ans;
    }
};

结果：
在这里插入图片描述

解法2：排序

如果将数组 nums 中的所有元素排序，那么下标为 numsSize/2 的元素一定是多数元素。

代码：

int cmpfunc (const void * a, const void * b)
{
   return ( *(int*)a - *(int*)b );
}
int majorityElement(int* nums, int numsSize){
    qsort(nums,numsSize,sizeof(int),cmpfunc);
    return nums[numsSize/2];
}

结果：
在这里插入图片描述

解法3：随机化

由于一个给定的下标对应的数字很有可能是众数，我们随机挑选一个下标，检查它是否是众数，如果是就返回，否则继续随机挑选。

代码：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        while(1)
        {
            int randNum=nums[rand()%nums.size()];
            int count=0;
            for(int num:nums)
            {
                if(num == randNum) count++;

            }
            if(count>nums.size()/2) return randNum;
        }
    }
};

结果：
在这里插入图片描述

解法4：Boyer-Moore 投票算法

思路：
如果我们把众数记为 +1，把其他数记为 -1，将它们全部加起来，显然和大于 0，从结果本身我们可以看出众数比其他数多。

算法：
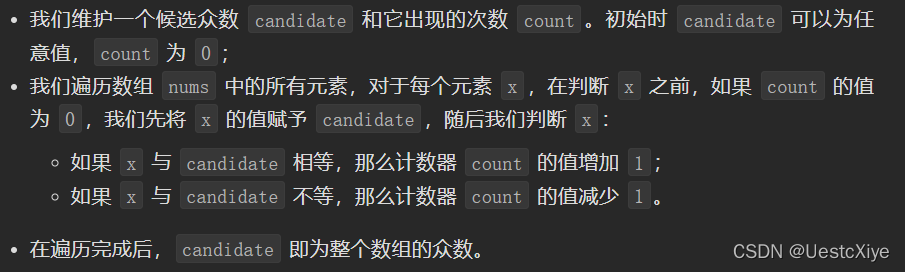
在这里插入图片描述

详情见：官方题解

代码：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int candidate=-1;
        int count=0;
        for (int num:nums)
        {
            if(num == candidate) count++;
            else if(--count<0)
            {
                candidate=num;
                count=1;
            }
        }
        return candidate;
    }
};