深度学习入门（七）：误差反向传播法

之前介绍的学习过程通过数值微分计算神经网络的权重参数，优点是容易实现，缺点是计算费时。
下面将介绍一个能够高效计算权重参数的梯度的方法。

计算图

计算图将计算过程用图形表示出来，即数据结构中的图，像，但又不完全像。
鱼书中给出了一个很鲜明的例子：

可以看到，先后进行了两次计算，从左至右。而且这个计算是累进的，先算总价，再算税后。

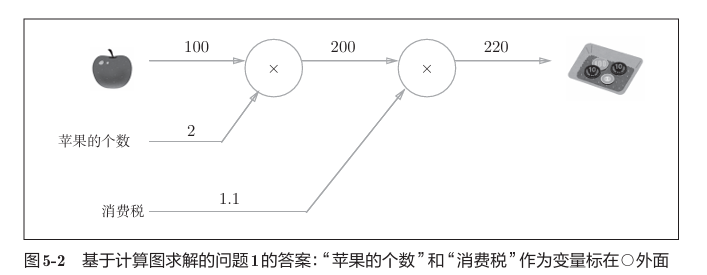
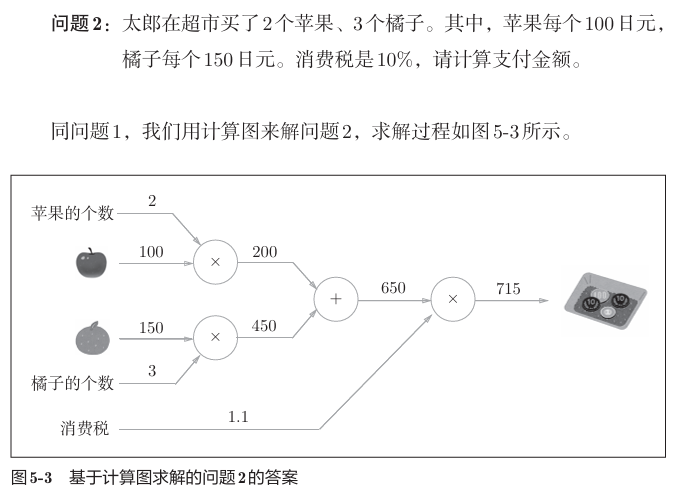
这里增加了加法结点，来计算合价。计算流程还是从左至右。综上，计算图解题的步骤如下：

1. 构建计算图。
2. 在计算图上从左向右进行计算。

这是一种正方向上的传播过程，简称为正向传播。当然，也存在反向传播，反向传播将在接下来的导数计算发挥重要作用。

局部计算

计算图的特征是可以传递“局部计算”获得最终结果。局部计算强调无论全局发生了什么，都只能根据与自己相关的信息输出接下来的结果。
也就是说，各个节点处只需进行自己有关的计算，不用考虑全局。
计算图可以集中精力于局部计算。无论全局的计算有多么复杂，各个步骤所要做的就是对象节点的局部计算。虽然局部计算非常简单，但是通过传递它的计算结果，可以获得全局的复杂计算的结果。
计算图将复杂的计算分割成简单的局部计算，和流水线作业一样，将局部计算的结果传递给下一个节点。

为什么用计算图解题

1. 无论全局是多么复杂的计算，都可以通过局部计算使各个节点致力于简单的计算，从而简化问题。
2. 利用计算图可以将中间的计算结果全部保存起来。
3. 可以通过反向传播高效计算导数。

例如，前面提到的问题中，想要求出结果随着输各个参数的变化的变化率，即导数。

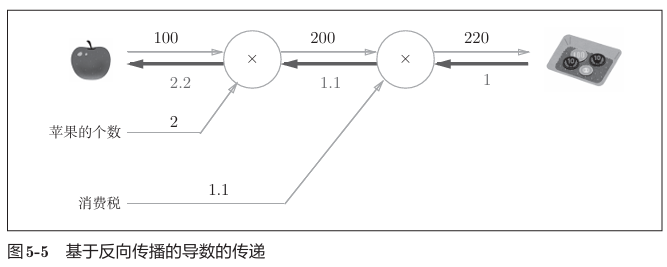
如图，反向传播传递“局部导数”，将导数的值写在箭头的下方。计算中途求得的导数的结果（中间传递的导数）可以被共享。

链式法则

从刚刚的反向传播的图示中，很明显能看出来存在链式传播的特点。

计算图的反向传播

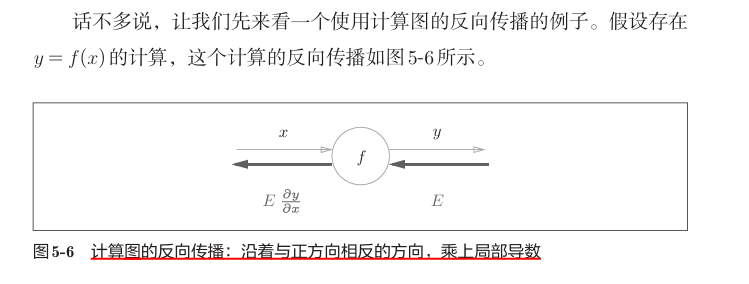
反向传播的计算顺序是，将信号E乘以节点的局部导数，然后将结果传递给下一个节点。

什么是链式法则

链式法则是关于复合函数的导数的性质，定义如下：
如果某个函数由复合函数表示，则该复合函数的导数可以用构成复
合函数的各个函数的导数的乘积表示。

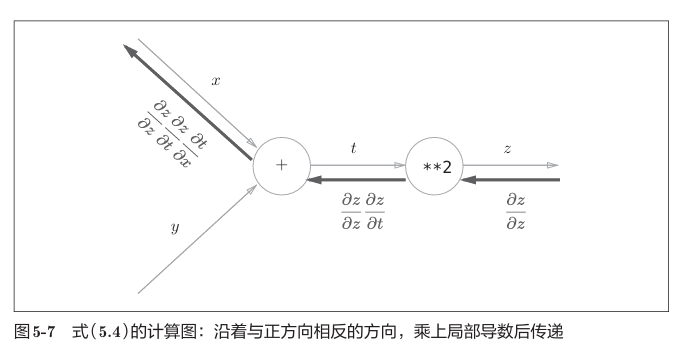
如图所示，计算图的反向传播从右到左传播信号。反向传播的计算顺序是，先将节点的输入信号乘以节点的局部导数（偏导数），然后再传递给下一个节点。

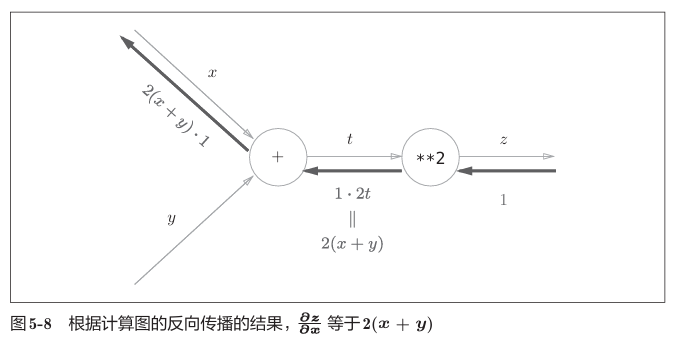
反向传播

加法节点的反向传播

反向传播将从上游传过来的导数，然后传向下游。也就是说，因为加法节点的反向传播只乘以1，所以输入的值会原封不动地流向下一个节点

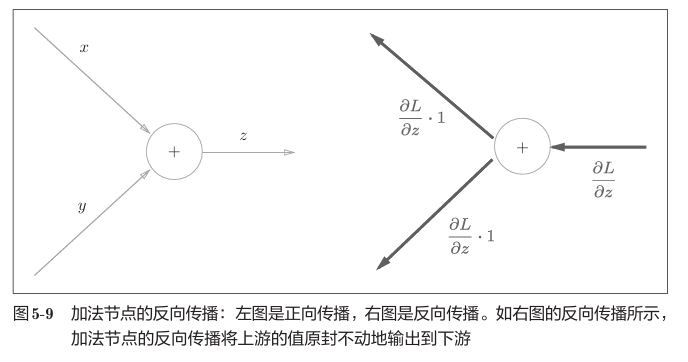
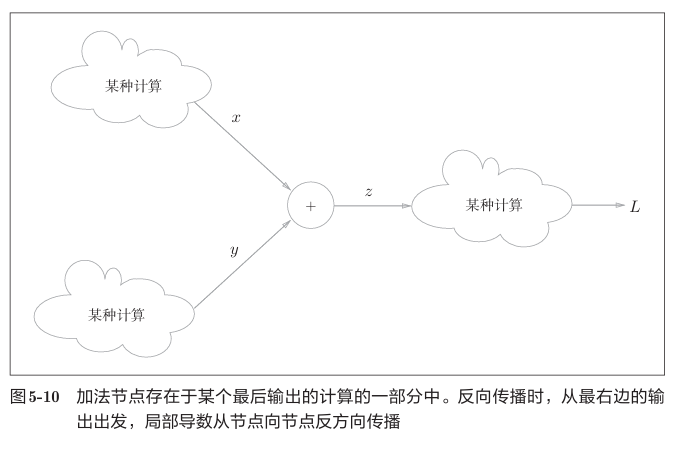
乘法节点的反向传播

乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。翻转值表示一种翻转关系。

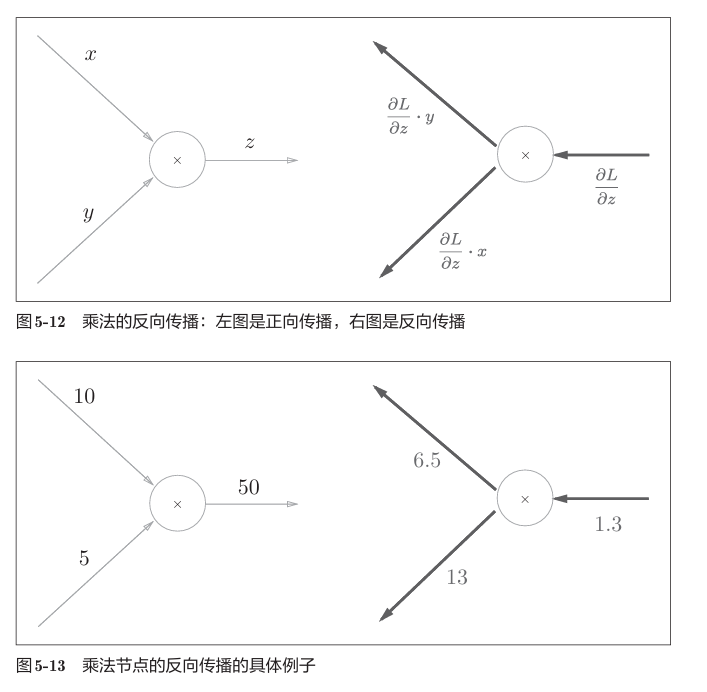
因为乘法的反向传播会乘以输入信号的翻转值，所以可以各自计算。另外，加法的反向传播只是将上游的值传给下游，并不需要正向传播的输入信号。但是，乘法的反向传播需要正向传播时的输入信号值。因此，实现乘法节点的反向传播时，要保存正向传播的输入信号。