前言
本篇文章原为笔者七升八数学论文作业,如有纰漏,请各位指出,在此感激不尽!
二维凸包的定义
我们先看一张图: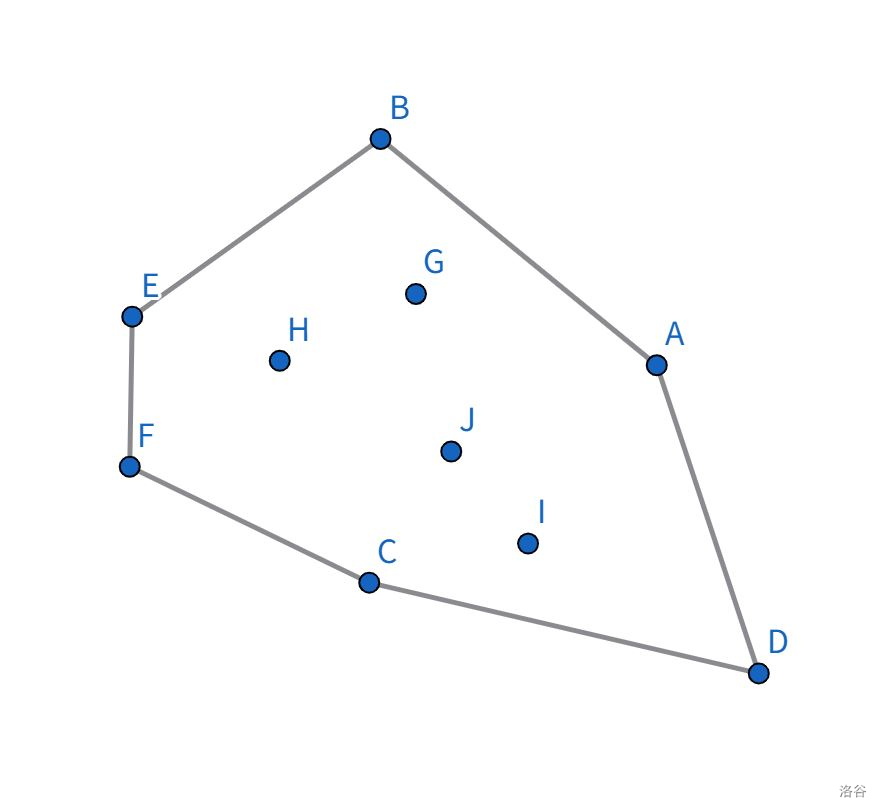
在这张图片里,一个平面上有数个点,同时还有一个凸多边形将这数个点完全覆盖,那么使这个图形面积最小的凸多边形就称为凸包。更具象化地讲,就是用手撑开一个橡皮筋并用其把一堆钉子围住,然后再松开手使橡皮筋收缩,那么最终橡皮筋形成的图形便是这些钉子的凸包。
二维凸包的求法
本文章主要介绍使用 Graham 算法求解二维凸包。
Graham 算法
我们先介绍几个前置知识;
- 极角
- 向量叉积
极角
极角指的是在极坐标中,平面上任意一点到极点的连线与极轴的夹角,如图:
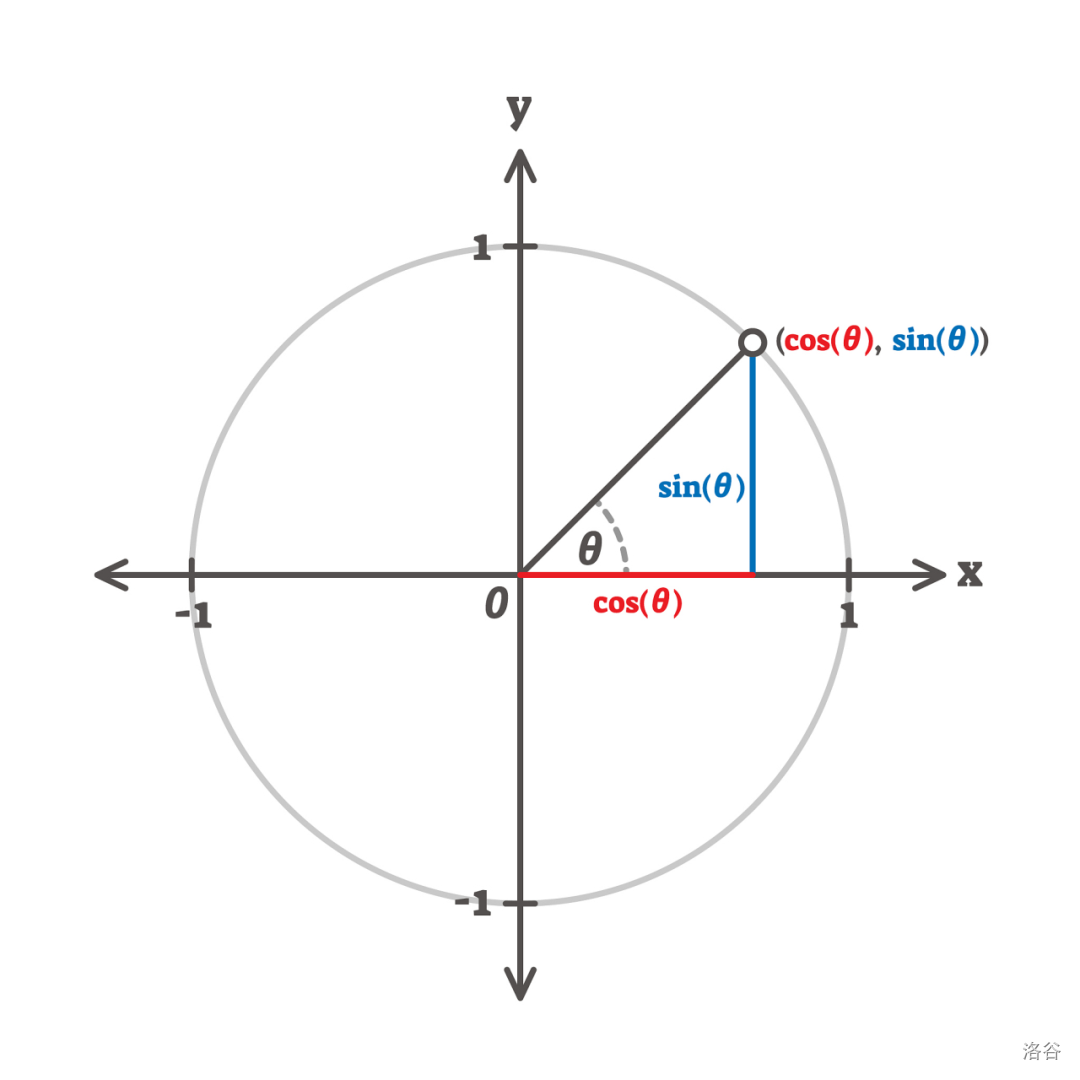
我们设 x x x 为 cos ( θ ) \cos(\theta) cos(θ), y y y 为 sin ( θ ) \sin(\theta) sin(θ)。则:
∵ tan ( y x ) = θ \because \tan(\frac{y}x) = \theta ∵tan(xy)=θ
∴ θ = arctan ( y x ) \therefore \theta = \arctan(\frac{y}x) ∴θ=arctan(xy)
这个公式在进行按极角大小排序时将会很有用。
向量叉积
向量叉乘是有大小有方向,并且不满足交换律的运算。在求解凸包的过程中,我们并不关心向量的大小,而是关心后者,即其方向。由于向量的运算满足右手法则,所以当两向量的叉积为正时,后一个向量便在前者的左边,在下文称之为左拐;否则,若两向量的叉积为负,那么后一个向量便在前者的右边,在下文称之为右拐。如下图:
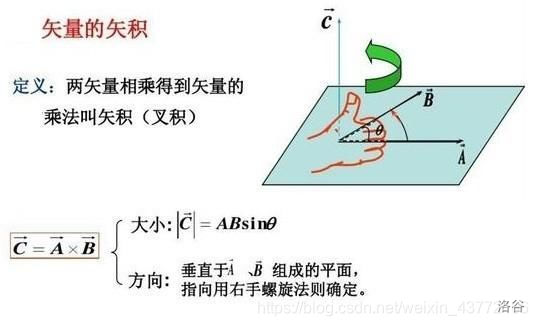
通过该运算,我们可以很清楚的判断两向量的位置关系,这在使用 Graham 算法求解凸包中发挥着很大的作用。
Graham 算法求解凸包
下面我将先介绍一下该算法求解凸包的流程:
- 首先选取一个 y y y 坐标最小的点作为起始节点,如果有多个点的 y y y 坐标相同,那就选择 x x x 坐标做小的点,此点必为凸包上的点。
- 令起始节点为极坐标原点,按平面内其它点的极角从小到大进行排序,如果极角相同,按其到原点的距离从大到小排序。
- 按排序后的顺序将原点和第一个点加入到一个栈中。
- 依次遍历排序后的点,每遍历到一个点时将栈顶的点和栈顶下面的点连线得到直线 l l l,然后判断遍历到的新点与栈顶元素所连成的直线与 l l l 为左拐、右拐或者处在同一直线上。如果是右拐或在同一直线上,则执行步骤五;否则执行步骤六。
- 栈顶元素不在凸包上,出栈,执行步骤四。
- 新点已处于凸包上,入栈。
- 如果此时排序后的最后一个点已入栈,那么算法结束,否则执行步骤四。
最后,栈中的所有元素便是凸包上的点了。
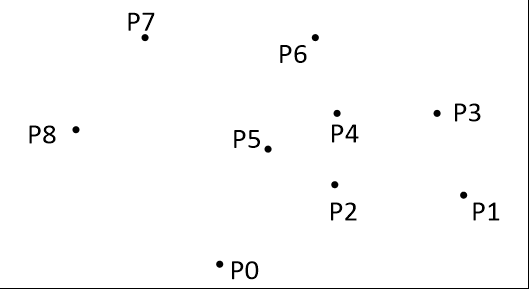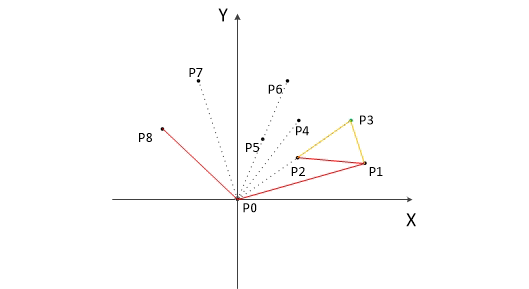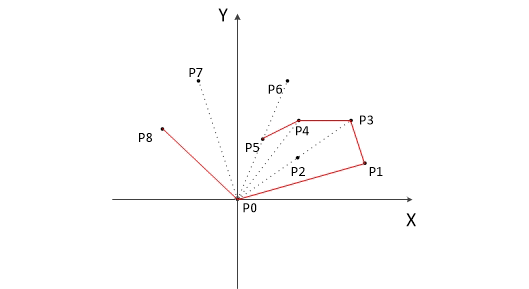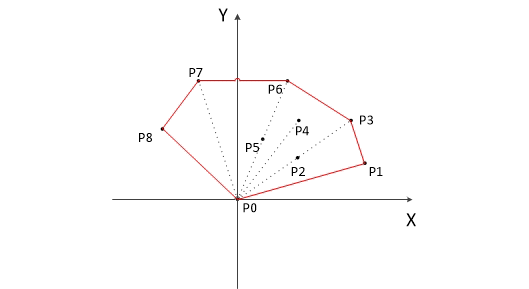
模拟算法流程的动图如下(在这幅图中先选取的时横坐标最小的点,但本质上都是一样的)::
正确性证明
我们将通过两个方面证明该算法正确性。
栈中所有点均为凸包顶点
- 原点为凸包顶点:因为原点 y y y 坐标以及 x x x 坐标均为最小的,所以它必然为凸包顶点。
- 栈中其它点均为凸包顶点:假设栈中有一点 p p p 不为凸包顶点,那么 p p p 必为凸包边上或内部一点。但因为每次遇到在同一直线上或者在栈顶元素连线的右边的点时都会弹出栈顶元素(即步骤四),这样,便使得凸包内部和边上的点均被弹出。所以凸包边上和内部的点必然不会在算法结束后出现在栈内。
凸包顶点均在栈内
假设凸包顶点 q q q 不在栈内,那么 q q q 必然在算法进行时存在后继点 q 1 q_1 q1 使得 q q q 和 q 1 q_1 q1 所连成的直线与 q q q 和原栈中的元素所连成的直线右拐。但因为在进行极角排序以后,凸包的顶点必然逆时针排列,即凸包的任意连续的三个顶点 p i − 1 , p i , p i + 1 p_{i-1}, p_i, p_{i+1} pi−1,pi,pi+1 均满足左拐。所以在处理凸包顶点 q q q 与后继节点 q 1 q_1 q1 时必满足左拐,所以 q q q 必然在栈内。
时间复杂度分析
在算法过程中极角排序的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),而每个点只会入栈和出栈一次,所以时间复杂度为 O ( n ) O(n) O(n)。总时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),效率较高。
代码实现(实现语言为 C++)
对于极角排序,我们可以使用内置的 atan2函数,即计算
arctan
\arctan
arctan 值。而每次判断栈顶元素是否需要出栈便相当于判断此时栈顶的两个点
A
A
A,
B
B
B 和 新点
C
C
C 是否满足
A
B
→
\overrightarrow{AB}
AB 与
B
C
→
\overrightarrow{BC}
BC 为左拐,这便是判断
A
B
→
×
B
C
→
≥
0
\overrightarrow{AB} \times \overrightarrow{BC} \ge 0
AB×BC≥0,我们可以使用向量叉积来判断。
以下 C++ 求解凸包的代码:
#include<bits/stdc++.h>
#define ll long long
#define inf (1ll << 62)
#define pb push_back
#define mp make_pair
#define PII pair<int , int>
#define fi first
#define se second
using namespace std;
struct Point {
long double x , y , a;
};
vector<Point>pos;
inline long double dis(Point a , Point b) {//计算两点距离
return sqrtl((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
inline long double cross(Point a , Point b) {//计算向量叉积
return a.x * b.y - b.x * a.y;
}
inline void solve() {
int n;
cin >> n;
for(int i = 0;i < n;i ++) {
long double x , y;
cin >> x >> y;
pos.pb({x , y , 0});
}
for(int i = 1;i < n;i ++) {//找出 y 坐标且 x 坐标最小的点
if(pos[i].y < pos[0].y || (pos[i].y == pos[0].y && pos[i].x < pos[0].x)) {
swap(pos[i] , pos[0]);
}
}
for(int i = 1;i < n;i ++) {//计算极角
pos[i].a = atan2(pos[i].y - pos[0].y , pos[i].x - pos[0].x);
}
sort(pos.begin() + 1 , pos.end() , [](Point &x , Point &y) {//极角排序
if(x.a == y.a) return dis(pos[0] , x) > dis(pos[0] , y);
return x.a < y.a;
});
vector<int>st(n + 1);
int top = 0;
st[++ top] = 0;
st[++ top] = 1;
for(int i = 2;i < n;i ++) {//维护栈
while(top >= 2 && cross({pos[st[top]].x - pos[st[top - 1]].x , pos[st[top]].y - pos[st[top - 1]].y} , {pos[i].x - pos[st[top]].x , pos[i].y - pos[st[top]].y}) < 0) top --;
st[++ top] = i;
}
long double ans = 0;
int last = 0;
for(int i = top;i >= 1;i --) {//计算凸包周长
ans += dis(pos[st[i]] , pos[last]);
last = st[i];
}
cout << fixed << setprecision(2) << ans << "\n";
return;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int t = 1;
// cin >> t;
while(t --) {
solve();
}
return 0;
}
二维凸包的应用
Graham 作为求解二维凸包的既经典、又高效的算法,在实际工程领域有着广泛的应用。接下来我们将举一个例子进行讨论:
自动驾驶汽车
现在自动驾驶汽车的开发十分迅速,这与现代社会的科技的进步密不可分,但是我们不难从中看到一些二维凸包的影子。
比如,当自动驾驶汽车经过施工路段时显然是需要识别路上的障碍标识的,并能在识别到行人时及时停下的。这怎么做到呢?我们可以在自动驾驶汽车车头的方位放置摄像头,然后当汽车遇到障碍物时摄像头便可以对每个聚类出来的障碍物云簇(簇:指用来描述一组具有相似特征的数据点集合),然后将其投射到二维平面上使用 Graham 算法计算俯视图的凸包。最终得到的凸多边形便精确的描绘了障碍物在地面上的投射范围。
所以,Graham 算法的存在,为现代科技发展提供了一定技术基础。
三维凸包
三维凸包在现阶段的主流做法主要为增量法,但能否有一种方法可以将 Graham 算法求解二维凸包的方法推广到求解三维凸包呢?
我们考虑 Graham 算法能处理的问题的特点:在同一平面内。所以我们是否能够将求解三维凸包的过程拆解成求解数个二维凸包然和将这些二维凸包合并在一起呢?具体来说,就是优先枚举在外围的点,这可以通过排序实现,然后每次枚举三个不共线点,求出其所在平面,然后枚举其它点,判断有多少个在该平面内,最后对所有在该平面内的点求解一遍二维凸包即可。
粗略的估算,时间复杂度是
O
(
n
4
×
n
log
n
)
O(n^4 \times n\log n)
O(n4×nlogn) 的,
n
4
n^4
n4 为枚举平面并判断点是否在平面内的时间。这样的时间复杂度是十分高的,算法效率很低,那有没有什么优化的方法呢?注意到一个平面内可能有很多的点,所以这个平面就会被枚举很多次,那是否可以令每个不同的平面只会被枚举一次呢?我们可以对每个点维护一个集合 set,初始时每个点的集合包含整个点集,然后每次通过
u
1
u_1
u1、
u
2
u_2
u2、
u
3
u_3
u3 三点确定一个平面后再通过枚举得出其它所在该平面的点集:
A
=
{
u
1
,
u
2
,
u
3
,
u
4
,
⋯
,
u
i
}
A=\{u_1,u_2,u_3, u_4,\cdots, u_i\}
A={u1,u2,u3,u4,⋯,ui}。那么此时就对
A
A
A 中的每一个点的集合
U
i
=
{
u
1
,
u
2
,
u
3
,
u
4
,
⋯
,
u
i
}
U_i=\{u_1,u_2,u_3,u_4,\cdots, u_i\}
Ui={u1,u2,u3,u4,⋯,ui} 都将
u
1
u_1
u1、
u
2
u_2
u2、
u
3
u_3
u3 删去。最后对于每个点
u
i
u_i
ui 我们只需要枚举所在其集合中的点就可以避免重复枚举平面。维护集合的时间复杂度是
O
(
log
n
)
O(\log n)
O(logn) 的,所以此时的总时间复杂度是:
O
(
V
n
log
2
n
)
O(Vn\log^2 n)
O(Vnlog2n),其中
V
V
V 为不同的平面的数量。
经过这样子的一个优化,现在的这个算法在求解较为稀疏的三维凸包时已经能够有了较好的表现,但实现的具体细节还需要具体的分析。如果想要更好的优化该算法的时间复杂度,那或许要等到未来进行进一步研究了。





















 332
332

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








