朴素贝叶斯Naive Bayesian分类器 (NBC)

诸神缄默不语-个人优快云博文目录

本文介绍常见的机器学习模型朴素贝叶斯Naive Bayesian。
朴素贝叶斯模型属于generative model，即通过输出的结果反推生成结果的模型概率。

1. 理论基础：贝叶斯定理

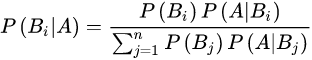
公式可以比较简单地从条件概率公式和全概率公式中推出来：$P\left(B_i|A\right)=\frac{P\left(A{B}_i\right)}{P\left(A\right)}=\frac{P\left(B_i\right)P\left(A|Bi\right)}{{\sum }_{j}P\left(A{B}_j\right)}$
这是个很典型的本科数学概率论与数理统计问题，此处不再赘述。

相关术语：
先验概率
后验概率

2. 原理

NBM假设影响类别的各项属性之间相互独立。

通过训练集学习从输入到输出的联合概率分布，再基于学习到的模型，输入 $X$ 求出使得后验概率最大的输出 $Y$

后验概率：

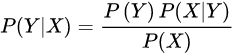
基于独立假设：

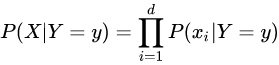
代入上式得：

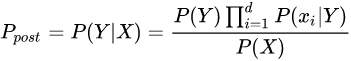
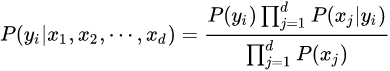
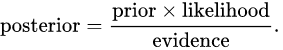
由于 $P(X)$ 恒定，因此在比较后验概率时只用比较分子部分。

最大后验概率（MAP）决策准则：

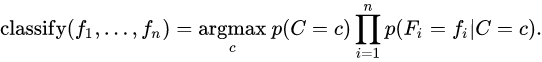
3. 算法

最大似然估计

类的先验概率可以通过假设各类等概率来计算（先验概率 = 1 / (类的数量)），或者通过训练集的各类样本出现的次数来估计（A类先验概率=（A类样本的数量）/(样本总数)）。为了估计特征的分布参数，我们要先假设训练集数据满足某种分布或者非参数模型。

高斯朴素贝叶斯：

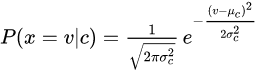
样本修正：如果一个给定的类和特征值在训练集中没有一起出现过，那么基于频率的估计下该概率将为0。这将是一个问题。因为与其他概率相乘时将会把其他概率的信息统统去除。所以常常要求要对每个小类样本的概率估计进行修正，以保证不会出现有为0的概率出现。

4. 本文撰写过程中使用的其他正文及脚注未提及的参考资料

1. 贝叶斯定理_百度百科
2. 朴素贝叶斯_百度百科
3. 朴素贝叶斯分类器 - 维基百科，自由的百科全书：这篇里面还给出了2个生动的例子。