文章探讨了如何合并二叉树，以及在二叉搜索树中进行搜索和验证的操作。重点是理解中序遍历在解决这类问题中的应用，如验证二叉搜索树的正确性，找到最小绝对差等。通过学习，作者发现局部到全局的递归策略和双指针技术能有效优化解题效率。
合并二叉树相对于中序加后序构造二叉树就简单很多
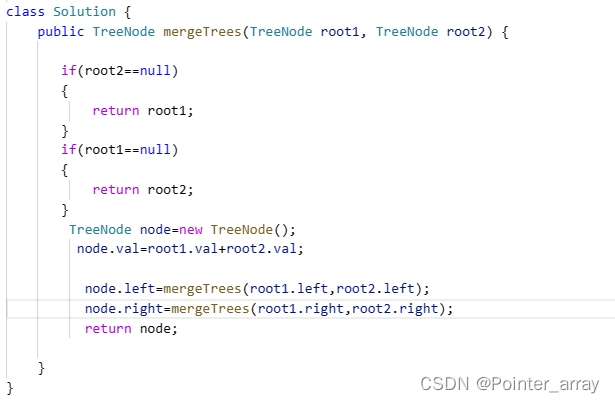
跟构建二叉树思路一样 建立一个node的结点
要先了解二叉搜索树的概念：比头结点小的值放入结点左边 比节点大的值放入节点右边
如果查到有该节点的子树就返回该结点
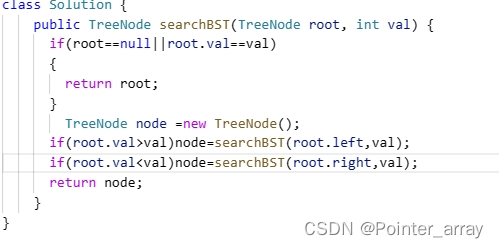
一开始不知道算法：中序遍历可以排序二叉搜索树
对于返回值的处理感觉脑子里还是一团浆糊
其实可已通过先分析局部 左右子树来确定递归的循环语句。
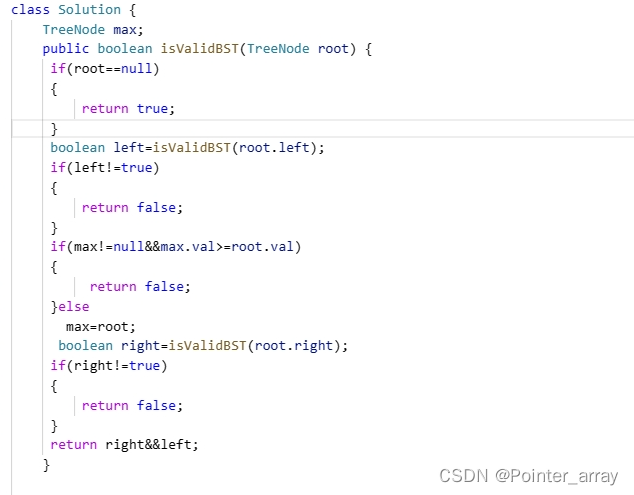
这个其实知道算法后还是挺简单的
中序遍历 首先判断左边是否含有结点 再判断中间的值是否大于该结点值如果不大于整体顺序不对返回false 再判断右边是否含有节点 如果遍历完所有节点都没问题就返回true
530. 二叉搜索树的最小绝对差 - 力扣（LeetCode）
没学双指针指向前面一个二叉树的结点时 我用了一个队列来解决改问题 虽然问题解决了但是时间上还是很差的
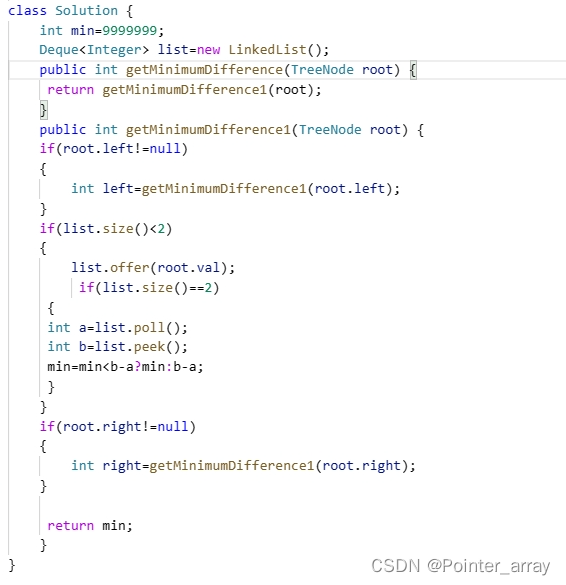
学了双指针建一个指向前面一个结点的指针就感觉非常巧妙
整体思路就是 用中序遍历 让下一个结点减去上一节点（因为搜索树所以中序遍历下 下减上能球最小值） 来比较最小值
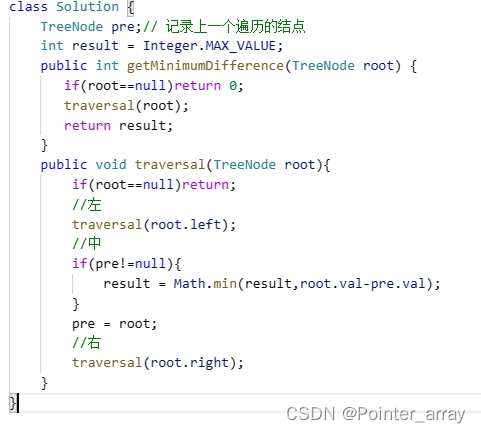
心得：解决二叉树的要领：首先判断参数和返回值 其次循环的终止条件 最后满足题目的算法和递归语句 特别的：递归语句可以先拿出子树进行局部判断再从局部解决个例再到整体。
扫一扫
940
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
