1. 支持向量机解决什么?
包含线性和非线性的模型,我们先在线性可分的数据样本集上找到一条分割不同样本集的线。然后再推广到线性不可分的数据样本集上

1.1 线性可分
上图我们可以看到线性可分可以找到一条线分割样本数据,但是这条线应该怎么找呢?
Vapnik(SVM发明者)提到
- 每一条线我们都可以计算一个性能指标:
将分割线平行的向左右移动,直到插到其中某一个(多个)样本点为止。而这两条线之前的距离就是这里说的性能指标,如图:

d 代表间隔(Margin)
两条平行线叉到的向量称为支持向量(Support Vectors),该算法做出来的分割线只跟支持向量有关!!!
- 性能指标最大的线,且该分割线在距离d的中心就是最优的分割线
那么求解这个最大化Margin即是一个优化问题(凸优化中的二次优化),对于SVM的优化问题可以看成
- 最小化 12∣∣w∣∣2\frac{1}{2}||w||^221∣∣w∣∣2
- 限制条件 yi[wTxi+b]≥1y_i[w^Tx_i + b] \geq 1yi[wTxi+b]≥1
二次优化的目标就相当于二次函数,而限制条件是一次项。是凸的,解的情况只可能无解或者有唯一解(不像非凸的有局部最值的情况)
凸函数定义:函数上任取两个点连成线,函数都应该在该条线的下方
看到这可能有读者就提出问题了,为什么最大化d能转变为最小化w⃗\vec ww的模长呢?下面来推导一下(看不懂记结论就好):
根据上面的理论描述,线性可分的定义如下:
假设我们的数据集(xi,yix_i,y_ixi,yi) 其中i∈(1,N)i \in (1,N)i∈(1,N),且是一个二分类问题,设定y的值仅为 1 或者 -1
∃(w⃗,b)使得对∀i∈(1,N)都有\exists (\vec w,b)使得对 \forall i \in (1,N) 都有∃(w,b)使得对∀i∈(1,N)都有
若yi=+1,则wTxi+b≥0若y_i = +1 ,则w^T x_i+ b \geq 0若yi=+1,则wTxi+b≥0
若yi=−1,则wTxi+b<0若y_i = -1 ,则w^Tx_i + b < 0若yi=−1,则wTxi+b<0
上面两条公式可以抽象得出(同正负符号抵消了)yi[wTxi+b]≥0 (1)y_i[w^Tx_i + b] \geq 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)yi[wTxi+b]≥0 (1)
首先需要了解如下两点
- (w⃗\vec ww,b)与 (aw⃗\vec ww,ab)是在同一超平面的,即是我们可以用常数a来进行缩放
- 任意一个向量x0x_0x0到超平面的距离可以表示如下distance=∣WTxo+b∣∣∣w∣∣=∣WTxo+b∣w12+w22+...+wn2distance = \frac{|W^Tx_o + b|}{||w||} = \frac{|W^Tx_o + b|}{\sqrt{w_1^2 + w_2^2 + ... + w_n^2}}distance=∣∣w∣∣∣WTxo+b∣=w12+w22+...+wn2∣WTxo+b∣
仔细看这个距离,通过缩放,我们完全可以找到一个(w⃗,b\vec w,bw,b)使得在支持向量x0x_0x0上有∣wTx0+b∣=1|w^Tx_0 + b| = 1∣wTx0+b∣=1 。此时上述距离就转变为distance=1∣∣w∣∣distance = \frac{1}{||w||}distance=∣∣w∣∣1
要使x0x_0x0与超平面距离最大,即∣∣w∣∣||w||∣∣w∣∣应该最小,优化问题第一点就是这么来的(前面的系数仅是为了求导方便,可以不加)
而另一条限制条件根据公式(1)结合线性可分的定义,我们知道除了支持向量,其他的向量应该有∣wTxi+b∣>1|w^Tx_i + b| > 1∣wTxi+b∣>1 ,整理合并就可以求得所有向量应该满足的条件,即是限制条件
1.2 线性不可分
通过线性可分得到的优化问题可以推广到线性不可分上即是
- 最小化 12∣∣w∣∣2+C∑i=1Nξi\frac{1}{2}||w||^2 + C\sum^N_{i=1} \xi_i21∣∣w∣∣2+C∑i=1Nξi
- 限制条件有两个分别是 yi[wTψ(xi)+b]≥1−ξiy_i[w^T\psi(x_i) + b] \geq 1 - \xi_iyi[wTψ(xi)+b]≥1−ξi 和 ξi≥0\xi_i \geq 0ξi≥0
其中C为超参(自己设定),ξi\xi_iξi为松弛变量, ψ(xi)\psi(x_i)ψ(xi)为高维映射,一般是无限维 (注意∀i∈(1,n)\forall i \in (1,n)∀i∈(1,n))。最小化式子中的后半项 C∑i=1NξiC\sum_{i=1}^N \xi_iC∑i=1Nξi 即为正则项,防止过拟合
支持向量机与其他算法不同的点在于它不寻找其他函数来拟合分界线,而是升维!!提高原本向量的维度,在高维空间中寻找分界线。如下图一个简单的例子演示,借助变换函数升高维度

然而ψ(xi)\psi(x_i)ψ(xi)是无限维的,对应wTw^TwT也是无限维的,这会使得问题边的很难解,这时候就要引出另外一个概念 — 核函数 (Kernel Function):
我们无需知道ψ(xi)\psi(x_i)ψ(xi)的显示表示,而是提供一个核函数,使得K(x1,x2)=ψ(x1)Tψ(x2)K(x_1,x_2) = \psi(x_1)^T\psi(x_2)K(x1,x2)=ψ(x1)Tψ(x2) (两个无限维的向量内积,结果是一个数,此时上面的优化问题就可解了)
注意:K要可拆必需满足如下两条
- K(x1,x2)=K(x2,x1) K(x_1,x_2) = K(x_2,x_1)~~~~~~K(x1,x2)=K(x2,x1) 即是可交换
- ∀ci,xi(i∈(1,N))\forall c_i , x_i (i \in (1,N))∀ci,xi(i∈(1,N)) 有 ∑i=1N∑j=1NcicjK(xi,xj)≥0 \sum^N_{i=1} \sum_{j=1}^Nc_ic_jK(x_i,x_j) \geq 0 ~~~~~~~~∑i=1N∑j=1NcicjK(xi,xj)≥0 半正定性
此时我们就可以将无限维的 ψ(xi)\psi(x_i)ψ(xi) 转化为核函数表示(通过原问题与对偶问题的转换,感兴趣的可以去听一听,这里就只写最终结论,图转自胡浩基老师的笔记)

2. 总结SVM算法
分为两步训练流程和测试流程
- 训练流程
输入{(xi,yix_i,y_ixi,yi)} 其中 i∈(1,N)i \in (1,N)i∈(1,N)
解优化问题
最大化: θ(α)=∑i=1Nαi−12∑i=1N∑j=1NαiαjyiyjK(xi,xj)限制条件: 0≤α≤c and ∑i=1Nαiyi=0最大化: ~~~~~~\theta(\alpha) = \sum^N_{i=1}\alpha_i - \frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_i\alpha_jy_iy_jK(x_i,x_j) \\ 限制条件:~~~ 0 \leq \alpha \leq c ~~~~~and ~~~~~\sum^N_{i=1}\alpha_iy_i = 0最大化: θ(α)=i=1∑Nαi−21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)限制条件: 0≤α≤c and i=1∑Nαiyi=0此时只有α\alphaα是未知参数,任是一个凸优化问题,求解出来后可以求b,即是找一个0<αi<c0<\alpha_i<c0<αi<c使得b=1−yi∑j=1NαjyjK(xi,xj)yib = \frac{1- y_i\sum^N_{j=1}\alpha_jy_jK(x_i,x_j)}{y_i}b=yi1−yi∑j=1NαjyjK(xi,xj) - 测试流程
输入测试样本 xxx,如果∑i=1NαiyiK(xi,x)+b≥0 , 则y=+1∑i=1NαiyiK(xi,x)+b<0 , 则y=−1\sum^N_{i=1}\alpha_iy_iK(x_i,x) + b \geq 0 ~~, ~~ 则 y = +1 \\ \sum^N_{i=1}\alpha_iy_iK(x_i,x) + b < 0 ~~, ~~ 则 y = -1i=1∑NαiyiK(xi,x)+b≥0 , 则y=+1i=1∑NαiyiK(xi,x)+b<0 , 则y=−1
2.1 内核函数的选择
常见的有如下三种
- Ploy – 多项式核 : K(x,y)=(xTy+1)d 其中d为参数K(x,y) = (x^Ty + 1)^d ~~~ 其中d为参数K(x,y)=(xTy+1)d 其中d为参数
- Rbf – 高斯径向基函数核 : K(x,y)=e∣∣x−y∣∣2σ2 其中σ为参数 K(x,y) = e^{\frac{||x-y||^2}{\sigma^2}} ~~~~ 其中\sigma为参数~~~~~~K(x,y)=eσ2∣∣x−y∣∣2 其中σ为参数 推荐👍
- Tanh – Tanh核 : K(x,y)=tanh(βxTy+b) 其中tanh(x)=ex−e−xex+e−xK(x,y) = tanh(\beta x^Ty + b) ~~~~~ 其中 tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}K(x,y)=tanh(βxTy+b) 其中tanh(x)=ex+e−xex−e−x
核函数里面的参数需要不断地去试,找到最好的
3. 交叉验证
一种验证数据集的方式
- 先分类:比如100,000个样本,我分成10类,每类10,000个样本点,此时N=10
- 每次从N中取出9类作为训练数据,剩下的一类作为测试数据。(此过程有N次,每次调用SVM训练)最终我们模型的测试结果就是 ∑i=1N测试识别率iN\frac{\sum^{N}_{i=1} 测试识别率_i}{N}N∑i=1N测试识别率i
4. ROC曲线
4.1 混淆矩阵

TP: 将正样本识别为正样本 FN: 将正样本识别为负样本
FP: 将负样本识别为正样本 TN: 将负样本识别为负样本
看前面的T还是F , T就说明我这步操作是正确的,F说明是错误的
且对同一个样本来说,TP越大,FP就越大!!(会越来越多负样本识别为正样本,下图所示)
其中 P(TP) + P(FN) = P(FP) + P(TN) = 1 (也就是一堆正样本,识别正确跟识别错误概率加起来是全集;负样本同理)
这时候我们就可以画出ROC曲线(FP - TP)
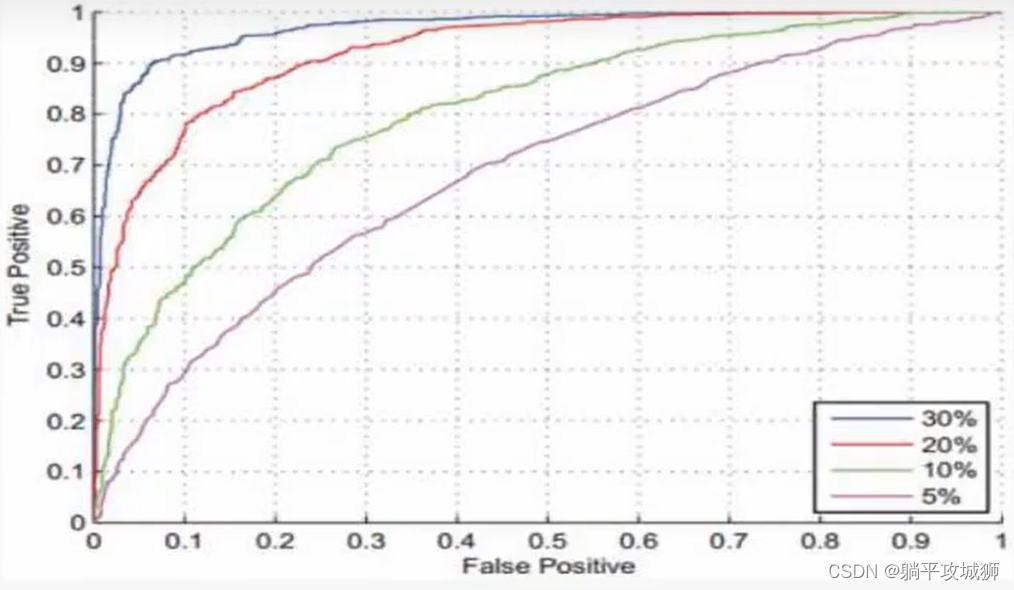 对于不同的模型ROC的看法不同,我们不能只根据识别率来判断好坏!!!
对于不同的模型ROC的看法不同,我们不能只根据识别率来判断好坏!!!
常用判断方法:
- 曲线做积分,即比较面积
- FP为0时候,比较TP,即是我不能容忍你把错误的看成正确的(譬如人脸识别,不能把陌生人放进来吧)
- 等错误率(EER):连接(0,1)(1,0)做一条直线 y+x = 1,切割曲线得到的交点,此点FP、FN相等,如果该EER越小,则模型越好
5. 多类问题
前面讲到的都是两个类,上升到多类问题的话我们需要:
- 一对其他类 N种
- 一对一 N(N−1)2~~~~~~~\frac{N(N-1)}{2} 2N(N−1)种 推荐👍
- 树形,即按分支来分,每一次跑一个分支决定在哪一大块内,再在内部细分




 本文介绍了支持向量机(SVM)的基本原理,包括如何在线性可分和线性不可分数据上工作,以及优化问题的转化。重点讲解了核函数的作用,展示了SVM的训练流程、测试流程,并讨论了内核函数的选择、交叉验证和ROC曲线在模型评估中的应用。
本文介绍了支持向量机(SVM)的基本原理,包括如何在线性可分和线性不可分数据上工作,以及优化问题的转化。重点讲解了核函数的作用,展示了SVM的训练流程、测试流程,并讨论了内核函数的选择、交叉验证和ROC曲线在模型评估中的应用。

















 1025
1025

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








