问题描述:
假设山洞中有n种宝物,每种宝物有一定重量w和相应的价值v,毛驴运载能力有限,只能运走m重量的宝物,一种宝物只能拿一样,宝物可以分割。那么怎么才能使毛驴运走宝物的价值最大呢?
问题分析:
与0-1背包问题类似,所不同的是在选择物品装入背包时,物品可分割,因此可按性价比(价值/质量)排序选择不同的物品。
0-1背包问题详见01背包问题_Player_HA的博客-优快云博客
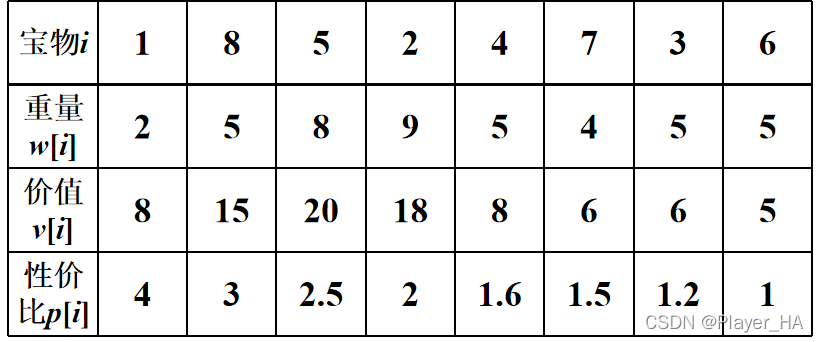
数据结构及初始化,将n种宝物的重量和价值存储在结构体three(包含重量、价值、性价比3个成员)中,同时求出每种宝物的性价比也存储在结构体three中,将其按照性价比从高到低排序。采用sum来存储毛驴能够运走的最大价值,初始化为0。
例如:
代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int M = 100000;
//背包结构体
struct three {
double w;//weight
double v;//value
double p;//性价比
}S[M];
bool cmp(three a, three b)//添加比较规则
{
return a.p > b.p;
}//降序排性价比
int main()
{
int n;//n个物品
double m;//承载能力
cout << "输入物品数量和承载能力:" << endl;
cin >> n >> m;
cout << "输入每个宝物的重量和价值:" << endl;
for (int i = 0; i < n; i++) {
cin >> S[i].w >> S[i].v;
S[i].p = S[i].v / S[i].w;//性价比
}
sort(S, S + n, cmp);//调用库中的函数sort cmp为比较方法
double sum = 0.0;//表示贪心记录运走宝物的价值
int m1 = m;
for (int i = 0; i < n; i++) {
if (m > S[i].w) {
m -= S[i].w;
sum += S[i].v;
}
else {
sum += S[i].p * m;
break;//容器已经装满,跳出循环
}
}
cout << "装得的最大价值:" << sum << endl;
cout << "装得的物品性价比:" << endl;
for (int i = 1; i <=n; i++)
{
cout << "["<<i<<"]:" << S[i].p << endl;
}
}
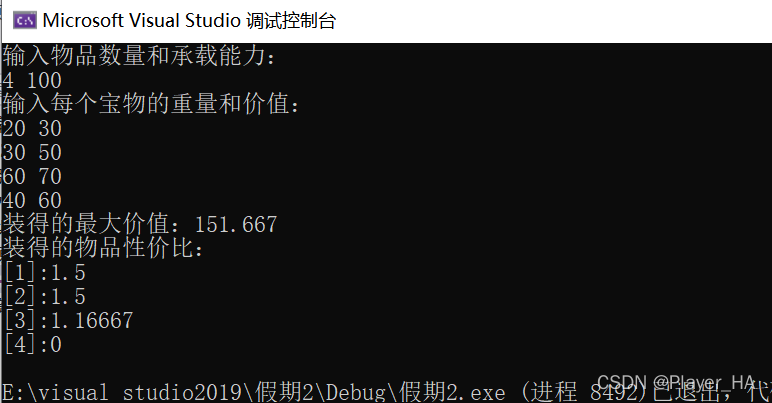







 该博客探讨了一个与0-1背包问题类似的问题,但允许宝物分割。通过计算每种宝物的性价比并进行排序,然后依次选取性价比最高的宝物直到毛驴的运载能力达到极限,以此最大化毛驴运输宝物的总价值。代码示例展示了如何实现这一优化策略,并输出了最大价值和所选宝物的性价比。
该博客探讨了一个与0-1背包问题类似的问题,但允许宝物分割。通过计算每种宝物的性价比并进行排序,然后依次选取性价比最高的宝物直到毛驴的运载能力达到极限,以此最大化毛驴运输宝物的总价值。代码示例展示了如何实现这一优化策略,并输出了最大价值和所选宝物的性价比。
















 982
982

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








