两个首尾对称序列的自相关

设确定性离散序列x1(n)、x2(n)的长度均为N，若序列x1(n)=[ x(0), x(1), …, x(N-2), x(N-1) ]，序列x2(n)=[ x(N-1), x(N-2), …, x(1), x(0) ]，则两个序列的自相关相等。

1. 结论证明

• 序列x1(n)的自相关
  
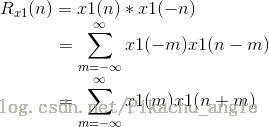
• 序列x2(n)的自相关
  
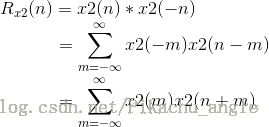
• n=0时
  $R_{x1}(n)=R_{x2}(n)=x(0)\cdot x(0)+x(1)\cdot x(1)+...+x(N-2)\cdot x(N-2)+x(N-1)\cdot x(N-1)$
• n=1时
  $R_x(n)=x(0)\cdot x(1)+x(1)\cdot x(2)+...+x(N-2)\cdot x(N-1)$
  $R_{x2}(n)=x(N-1)\cdot x(N-2)+x(N-2)\cdot x(N-3)+...+x(1)\cdot x(0)$
  所以，n=1时，$R_{x1}(1)=R_{x2}(1)$。
• n=2时
  $R_{x1}(n)=x(0)\cdot x(2)+x(1)\cdot x(3)+...+x(N-3)\cdot x(N-1)$
  $R_{x2}(n)=x(N-1)\cdot x(N-3)+...+x(3)\cdot x(1)+x(2)\cdot x(0)$
  所以，n=2时，$R_{x1}(2)=R_{x2}(2)$。
• n=i ( i=0, 1, …, N-1 )时
  …
• n=N-1时
  $R_{x1}(N-1)=R_{x2}(N-1)=x(0)\cdot x(N-1)$
  综上所述，$R_{x1}(n)=R_{x2}(n)$，即两个序列的自相关相等。

2. 程序代码

clc
clear all
close all

N=3;
x=[1 2 3];
y=[3 2 1];
rxx=xcorr(x);              %x的自相关序列
ryy=xcorr(y);              %y的自相关序列
Rxx=zeros(N);
Ryy=zeros(N);
for i=1:N                  %x的自相关矩阵
    for j=1:N
        Rxx(i,j)=rxx(N+i-j);
    end
end
for i=1:N                  %y的自相关矩阵
    for j=1:N
        Ryy(i,j)=ryy(N+i-j);
    end
end
Rxx
Ryy

3. 仿真结果
   
   仿真结果与理论证明一致，验证了该理论的正确性。