1.问题
设p1=(x1,y1),p2=(x2,y2)…pn=(xn,yn)是平面n上n个点构成的集合S,最近对问你就是找出集合S中距离最近的点对。
2.解析
暴力法:
在蛮力法实现最近点对问题中,将问题简化:距离最近的点对可能多于一对,找出一对即可,另外只考虑二维平面中的情况。用距离公式即可求
分治法:
分治法思想解决此问题时,首先考虑将最近对问题进行分治,设计其分治策略。将集合S分成两个子集S1和S2,根据平衡子问题原则,每个子集中的点数大致都为n/2。这样分治后,最近点对将会出现三种情况:在S1中,在S2中或者最近点对分别在集合S1和S2中。利用递归分析法分别计算前两种情况,第三种方法另外分析。求解出三类子情况后,再合并三类情况,比较分析后输出三者中最小的距离。
3.设计
暴力法:
double closestPoints(double x[],double y[],int n){
double x1,x2,y1,y2;
double dist,minDist=MAX;
for(int i=0;i<n;i++)
for(int j=i+1;j<n;j++){
dist=(x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);
if(dist<minDist){
minDist=dist;
x1=x[i];y1=y[i];
x2=x[j];y2=y[j];
}
}
printf(“%d,%d - %d %d”,x1,y1,x2,y2)
return minDist;
}
分治法:
// 求两点间的距离
double getDis(Building bA, Building bB)
{
double dDifferenceX = bA.x - bB.x;
double dDifferenceY = bA.y - bB.y;
return sqrt(dDifferenceX*dDifferenceX + dDifferenceY*dDifferenceY);
}
// 求所有点间的距离
double* getAllDis(Building* abCoordinate, int iBuilNum, int iDisNum, int* aiMinIndex)
{
int i, j, k;
double dMin = 1000.0;
double* adDis = (double*)malloc(sizeof(double)*iDisNum);
for(i=iBuilNum-1, k=0; i>0; i--)
{
for(j=i; j>0; j--)
{
adDis[k] = getDis(abCoordinate[iBuilNum-i-1], abCoordinate[iBuilNum-j]);
// 截取最小距离
if(adDis[k] < dMin)
{
dMin = adDis[k];
// 截取最小距离相应坐标数组的下标
aiMinIndex[0] = iBuilNum-i-1;
aiMinIndex[1] = iBuilNum-j;
}
k++;
}
}
return adDis;
}
4.分析
暴力法:
通过遍历所有点集,计算出每一个点对的距离,计算出最近的距离并输出。避免同一对点计算两次,只考虑i<j的点对(pi,pj)。
其主要循环的步骤就是求出平方值,执行的次数为:
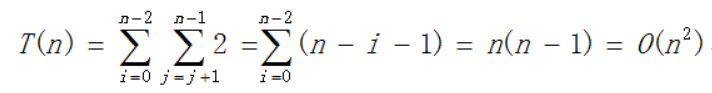
分治法:
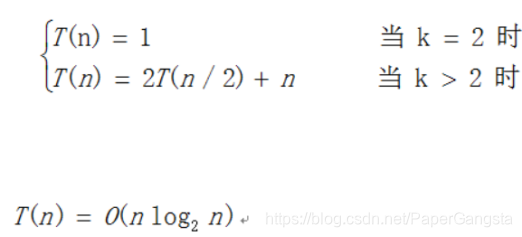




 本文探讨了平面中寻找距离最近点对的问题,介绍了暴力法和分治法两种解决方案。暴力法通过遍历所有点对计算距离,而分治法采用递归策略,将点集分为两部分,分别在各部分及跨部分寻找最近点对。
本文探讨了平面中寻找距离最近点对的问题,介绍了暴力法和分治法两种解决方案。暴力法通过遍历所有点对计算距离,而分治法采用递归策略,将点集分为两部分,分别在各部分及跨部分寻找最近点对。
















 2349
2349

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








