本文介绍了多视图几何中如何通过八点法将二次型xTEy转化为线性形式BElinear，解释了矩阵操作过程，并阐述了本质矩阵求解中关键的齐次线性方程组和最小二乘方法的应用。讨论了特征点对数与矩阵维度的关系，以及8点法的重要性。
在多视图几何的 2D 几何中，在利用八点法（Eight-point-algorithm）求解本质矩阵（Essential Matrix）的时候，出现一个将 类似二次型的形式：
x
T
E
y
\mathbf{x}^{T}E\mathbf{y}
xTEy
将其表示成
B
E
l
i
n
e
a
r
BE_{linear}
BElinear
的过程
其中，
B
B
B的元素 仅与
x
,
y
\mathbf{x},\mathbf{y}
x,y有关。
下面首先简单地推导该过程，接着复习一下二次型相关内容
“线性化”二次型
我将这个过程称之为 “线性化”，主要是因为它将矩阵
E
E
E 处理成一个向量。
在这里，矩阵
E
E
E 是需要求解的未知数。
而
x
,
y
\mathbf{x},\mathbf{y}
x,y 则是在两个视图上的匹配特征点的坐标信息。
0
=
[
x
1
x
2
x
3
]
[
e
11
e
12
e
13
e
21
e
22
e
23
e
31
e
32
e
33
]
[
y
1
y
2
y
3
]
0=\begin{bmatrix} x_1&x_2&x_3 \end{bmatrix} \begin{bmatrix} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} &e_{23} \\ e_{31} & e_{32} & e_{33} \end{bmatrix} \begin{bmatrix} y_1\\y_2\\y_3 \end{bmatrix}
0=[x1x2x3]⎣
⎡e11e21e31e12e22e32e13e23e33⎦
⎤⎣
⎡y1y2y3⎦
⎤
= [ x 1 e 11 + x 2 e 21 + x 3 e 31 x 1 e 12 + x 2 e 22 + x 3 e 32 x 1 e 13 + x 2 e 23 + x 3 e 33 ] [ y 1 y 2 y 3 ] (1) =\begin{bmatrix} x_1e_{11} +x_2e_{21}+x_3e_{31}& x_1e_{12} +x_2e_{22}+x_3e_{32}& x_1e_{13} +x_2e_{23}+x_3e_{33} \end{bmatrix}\begin{bmatrix} y_1\\y_2\\y_3 \end{bmatrix} \tag{1} =[x1e11+x2e21+x3e31x1e12+x2e22+x3e32x1e13+x2e23+x3e33]⎣ ⎡y1y2y3⎦ ⎤(1)
= [ x 1 y 1 e 11 + x 2 y 1 e 21 + x 3 y 1 e 31 + x 1 y 2 e 12 + x 2 y 2 e 22 + x 3 y 2 e 32 + x 1 y 3 e 13 + x 2 y 3 e 23 + x 3 y 3 e 33 ] (2) =\begin{bmatrix}x_1y_1e_{11} +x_2y_1e_{21}+x_3y_1e_{31}+x_1y_2e_{12} +x_2y_2e_{22}+x_3y_2e_{32}+ x_1y_3e_{13} +x_2y_3e_{23}+x_3y_3e_{33}\end{bmatrix} \tag{2} =[x1y1e11+x2y1e21+x3y1e31+x1y2e12+x2y2e22+x3y2e32+x1y3e13+x2y3e23+x3y3e33](2)
注意：式（2）是一个
1
×
1
1\times1
1×1 的矩阵。
观察式（3）的结构，将式（2）重写：
=
[
x
1
y
1
x
1
y
2
x
1
y
3
x
2
y
1
x
2
y
2
x
2
y
3
x
3
y
1
x
3
y
2
x
3
y
3
]
[
e
11
e
12
e
13
e
21
e
22
e
23
e
31
e
32
e
33
]
(3)
=\begin{bmatrix} x_1y_1 & x_1y_2 &x_1y_3&x_2y_1 & x_2y_2 &x_2y_3&x_3y_1 & x_3y_2 &x_3y_3 \end{bmatrix} \begin{bmatrix} e_{11} \\ e_{12}\\e_{13}\\e_{21} \\ e_{22}\\e_{23}\\e_{31} \\ e_{32}\\e_{33} \end{bmatrix} \tag{3}
=[x1y1x1y2x1y3x2y1x2y2x2y3x3y1x3y2x3y3]⎣
⎡e11e12e13e21e22e23e31e32e33⎦
⎤(3)
每增加一对特征点，都可以写出一个如式（3）所示的约束。
可以把它们都拼凑起来。得到一个齐次线性方程组。
在这里就不展示拼凑之后的方程组了
求解本质矩阵最少需要 8 对特征点
根据线性代数的基本知识（Rank-Nullity Theorem），
在齐次线性方程组
E
m
×
9
∗
e
=
0
⃗
(4)
E_{m\times 9}* \mathbf{e} =\vec{0}\tag{4}
Em×9∗e=0(4)
其中，
e
=
[
e
11
e
12
e
13
e
21
e
22
e
23
e
31
e
32
e
33
]
\mathbf{e} = \begin{bmatrix} e_{11} \\ e_{12}\\e_{13}\\e_{21} \\ e_{22}\\e_{23}\\e_{31} \\ e_{32}\\e_{33}\end{bmatrix}
e=⎣
⎡e11e12e13e21e22e23e31e32e33⎦
⎤
齐次线性方程组基础解系的秩+矩阵
E
E
E 的秩 = 9。
向量
e
\mathbf{e}
e 位于矩阵
E
E
E 的零空间中。如果系数矩阵是满秩的（即秩为8），那么它的零空间维数为 1，也就是
e
\mathbf{e}
e 构成一条线。这与
e
\mathbf{e}
e 的尺度等价性是一致的。
所以我们想要矩阵 A 的秩为 8，那么矩阵 A 要有 8 个线性无关的行向量，
那么 m m m 至少为8。
那么至少需要 8 对匹配的特征点。
所以 8 点法应运而生。
最小二乘与线性方程组求解
上述问题会转化为一个线性方程组的求解问题，我们需要求解下列线性方程组
A
e
=
0
⃗
\mathbf{Ae}=\vec{0}
Ae=0
其中
A
\mathbf{A}
A 是一个
m
×
9
m\times 9
m×9 的矩阵
但是当 m >= 9 的时候，即匹配点为 9 个或者 9 个以上时，不一定存在 e \mathbf{e} e 使得上式成立。
因此此时通过最小化一个二次型来求
min
e
∥
A
e
∥
2
2
=
min
e
e
T
A
T
A
e
\min_{\mathbf{e}} \Vert \mathbf{Ae} \Vert ^2_2=\min_{\mathbf{e}} \mathbf{e}^{ T}\mathbf{A}^{T}\mathbf{Ae}
emin∥Ae∥22=emineTATAe
上式成立实际上是因为有下式成立
∥
y
⃗
∥
2
2
=
y
⃗
T
y
⃗
\Vert \vec{y} \Vert ^2_2= \vec{y}^{T}\vec{y}
∥y∥22=yTy
二次型复习
上面推导过程涉及的不是二次型，只是类似二次型，因为二次型是
x
T
E
x
\mathbf{x}^TE\mathbf{x}
xTEx
而上面的是
x
T
E
y
\mathbf{x}^TE\mathbf{y}
xTEy。
这两种形式的结果都是一个
1
×
1
1\times1
1×1 的矩阵。
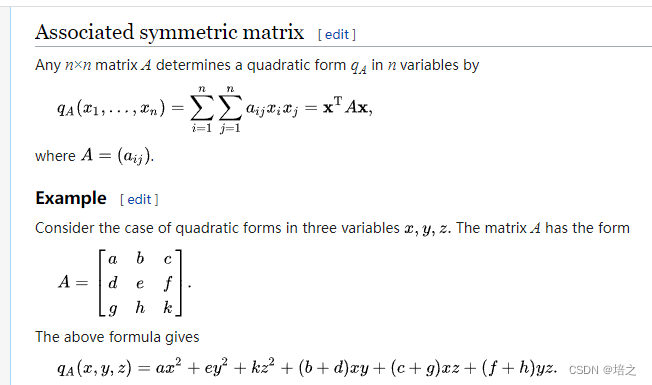
So, two different matrices define the same quadratic form if and only if they have the same elements on the diagonal and the same values for the sums
b
+
d
c
+
g
{b+d}{c+g}
b+dc+g and
f
+
h
{ f+h}
f+h In particular, the quadratic form
q
A
{ q_{A}}
qA is defined by a unique symmetric matrix
扫一扫
1809
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
