动态规划 c++ 数字三角形

---

• Description
  

---

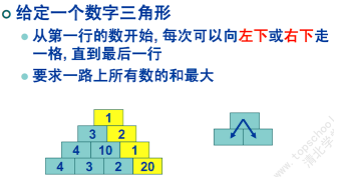
• Format Input
  第一行一个整数N(<=1000)，表示三角形总共有几行 第二至第N+1行，给出这个数字三角形
• Format Output
  一个整数，表示一路上所有数的最大和，结果不会超过int64

---

• Sample Input
  4
  1
  3 2
  4 10 1
  4 3 2 20
• Sample Output
  24

---

没学过dp的码友看完题是不是一脸懵？没关系，接下来我呈上自己的思路

先看题目。我们做编程题的主要思路中，有一个很重要的思路，就是从小推到大。那在这题中使用：
首先一层的情况不用讨论，相信有脑子的都会

然后看两层，我们是从上往下走求和，那就有两种方法：向左~ 向右~ 然后取一个更大的。

那么很明显，需要用一个数组存下从最高层走到这个点上的最大数字和。这里用f[i][j]表示从第一行第一列到第i行第j列的最大数字和。这样，动态规划的第一个要点：所求状态就明确了。

---

然后接下来要求的是状态转移方程。f[i][j]可能是从左上f[i-1][j-1]来的，也可能是从右上f[i-1][j]来的，而我们要求的是最大答案，所以要用到一个max函数。

{
   
	f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a