线性代数：SVD分解【用于信息压缩&降噪】

矩阵的SVD分解- Singular Value Decomposition【矩阵的奇异值分解】
优点：适用于任意形状的矩阵，是 特征分解 在任意矩阵上的推广

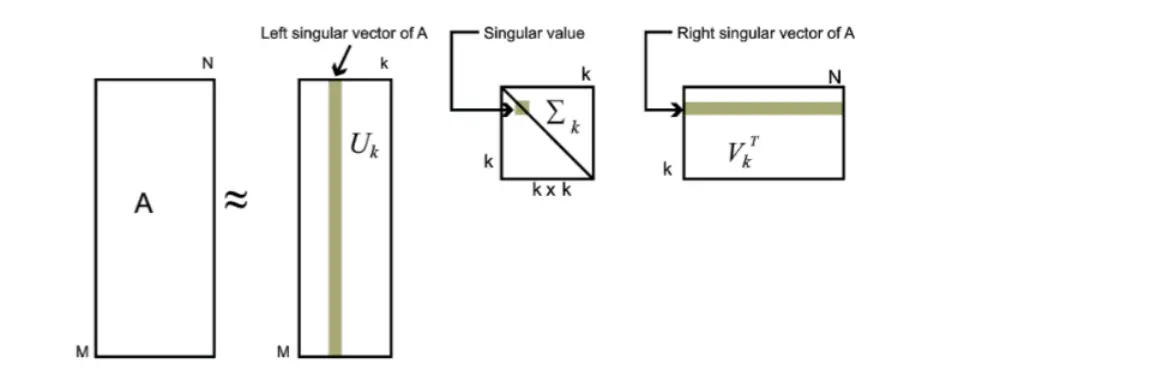
分解形式
$$A=U\Sigma V^T$$
$A=\left[\begin{array}{cccc}|& |& & |\\ {\vec{u}}_1& {\vec{u}}_2& ...& {\vec{u}}_m\\ |& |& & |\end{array}\right]\left[\begin{array}{ccccc}{\sigma }_1& & & & \\ & {\sigma }_2& & & 0\\ & & ...& & \\ 0& & & {\sigma }_r& \\ & 0& & & 0\end{array}\right]\left[\begin{array}{ccc}-& {\vec{v}}_1& -\\ -& {\vec{v}}_2& -\\ & & \\ -& {\vec{v}}_n& -\end{array}\right]$
对于$m\ast n$的$A$矩阵，则$U$是$m\ast m$的方阵(左奇异矩阵)；$\Sigma$是$m\ast n$的长方阵(奇异值矩阵)；$V$是$n\ast n$的方阵(右奇异矩阵)

$V$是$A^{T}A$的标准化特征向量矩阵，是一个标准正交矩阵，$V=V^T$

$U$是$A$的列空间的一组标准正交基构成的矩阵 $U=\left[\begin{array}{cccc}|& |& & |\\ {\vec{u}}_1& {\vec{u}}_2& ...& {\vec{u}}_m\\ |& |& & |\end{array}\right]$由前$r$个从大到小排列的奇异值且不为零的奇异值对应的$\vec{u}$向量从左到右排列构成，根据矩阵的列空间定义 $(r\le m)$，${\vec{u}}_i=\frac{A{\vec{v}}_i}{{\sigma }_i}{\sigma }_i\ne 0$；所以当$r<m$的时候要构造一个$m\ast m$的方阵$U$需要补充到$m$个$\vec{u}$向量，缺失的$\vec{u}$向量可以通过 Gram-Schmidt 方法找到$m-r$个向量，使得这$m$个$\vec{u}$向量两两互相垂直。所以$U$矩阵也是一个标准正交矩阵。
  \,
$\Sigma$ 矩阵是一个$m\ast n$奇异值矩阵，对角线由从大到小排列的奇异值按从上到小的顺序填充而成，由于$r\le m$，缺失行由零向量填充,其左上角是一个$r\ast r$对角矩阵
$\Sigma =\left[\begin{array}{ccccc}{\sigma }_1& & & & \\ & {\sigma }_2& & & 0\\ & & ...& & \\ 0& & & {\sigma }_r& \\ & 0& & & 0\end{array}\right]=\left[\begin{array}{cc}D& 0\\ 0& 0\end{array}\right]$
  \,
SVD与特征值分解的联系： $A^{T}A=(U\Sigma V^T{)}^T\cdot (U\Sigma V^T)=V^T{\Sigma }^{2}V=PD{P}^T$

证明

对于 $A=U\Sigma V^T$
左乘$V$则有$AV=U\Sigma V^{T}V$，标准正交矩阵中$V^TV = I \rightarrow AV = U\Sigma $ ，该数学形式与方阵特征值分解类似。
$\because {\vec{v}}_i$ 是$A^{T}A$的标准特征向量 ，$AV=A\left[\begin{array}{cccc}|& |& & |\\ {\vec{v}}_1& {\vec{v}}_2& ...& {\vec{v}}_n\\ |& |& & |\end{array}\right]=\left[\begin{array}{cccc}|& |& & |\\ A{\vec{v}}_1& A{\vec{v}}_2& ...& A{\vec{v}}_n\\ |& |& & |\end{array}\right]$

又${\vec{u}}_i=\frac{A{\vec{v}}_i}{{\sigma }_i}$,其中${\sigma }_i=\sqrt{\Vert A\cdot {\vec{v}}_i{\Vert }^2}=\sqrt{{\lambda }_i}$，当存在$\sigma =0\to \sigma \vec{u}=0$，从而
$AV=\left[\begin{array}{cccc}|& |& & |\\ A{\vec{v}}_1& A{\vec{v}}_2& ...& A{\vec{v}}_n\\ |& |& & |\end{array}\right]=\left[\begin{array}{cccccc}|& |& & |& & \\ {\sigma }_1{\vec{u}}_1& {\sigma }_2{\vec{u}}_2& ...& {\sigma }_r{\vec{u}}_r& ...& 0\\ |& |& & |& & \end{array}\right]$

$U\Sigma =\left[\begin{array}{cccc}|& |& & |\\ {\vec{u}}_1& {\vec{u}}_2& ...& {\vec{u}}_m\\ |& |& & |\end{array}\right]\left[\begin{array}{ccccc}{\sigma }_1& & & & \\ & {\sigma }_2& & & 0\\ & & ...& & \\ 0& & & {\sigma }_r& \\ & 0& & & 0\end{array}\right]=\left[\begin{array}{cccccc}|& |& & |& & \\ {\sigma }_1{\vec{u}}_1& {\sigma }_2{\vec{u}}_2& ...& {\sigma }_r{\vec{u}}_r& ...& 0\\ |& |& & |& & \end{array}\right]$

$\therefore AV=U\Sigma \to A=U\Sigma V^T$

算法过程

对于任意一个矩阵$A$,求解$U\Sigma V^T$
step.1 求解$A^{T}A$的特征值和特征向量;
step.2 对$A^{T}A$的非零特征值$\lambda$ 进行开根得到奇异值$\sigma$，顺序填充成$m\ast n$的奇异值矩阵$\Sigma$;
step.3 $A^{T}A$的特征向量标准化处理后，这些标准特征向量按从大到小的特征值对应关系按列填充成$n\ast n$的$V$,取$V^T$;
step.4 ${\vec{u}}_i=\frac{A{\vec{v}}_i}{{\sigma }_i}$在经过Gram-Schmidt扩展填充成$U$

SVD应用

1.几何坐标变换

$A=U\Sigma V^T$ 若A是$m\ast n$的矩阵 $A$将对一个$n$维向量转换成$m$维的向量；

$V$是$n$维空间的一组标准正交基，从而$n$维空间中的任意向量$\vec{x}$可以被$V$中的列向量所组合表示$\vec{x}=k_1{\vec{v}}_1+k_2{\vec{v}}_2+...+k_n{\vec{v}}_n=V\vec{k}$ ，这里$V\vec{k}$中的向量$\vec{k}$即$V$坐标系下每个维度上的坐标值。

而$n$维空间的向量$\vec{x}$被$A$变换将得到:
$A\vec{x}=U\Sigma V^T\vec{x}=U\Sigma V^T\cdot V\vec{k}=U\Sigma \vec{k}=U\left[\begin{array}{c}{\sigma }_1{k}_1\\ ...\\ {\sigma }_r{k}_r\\ 0\end{array}\right]$
在这里变换后表明在$U$坐标系下，原来$V$坐标系下的向量$\vec{x}$坐标值将被拉伸$\sigma$倍。

2.数据压缩去噪降维

奇异值分解与特征值分解的目的一样，都是提取出一个矩阵最重要的特征。
所有的矩阵都可以进行奇异值分解，但只有方阵才可以进行特征值分解。当所给的矩阵是对称的方阵，，二者的结果是相同的。所以对称矩阵的特征值分解是奇异值分解的一个特例。对于奇异值，它跟特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。所以可以应用最大的k个的奇异值和对应的左右奇异矩阵来近似描述矩阵达到 denoise 的目的。

SVD降噪数学展开式$A=U\Sigma V^T$
$\left[\begin{array}{cccccc}|& |& & |& & \\ {\sigma }_1{\vec{u}}_1& {\sigma }_2{\vec{u}}_2& ...& {\sigma }_r{\vec{u}}_r& ...& 0\\ |& |& & |& & \end{array}\right]\left[\begin{array}{ccc}-& {\vec{v}}_1& -\\ -& {\vec{v}}_2& -\\ & & \\ -& {\vec{v}}_n& -\end{array}\right]={\sigma }_1{\vec{u}}_1{\vec{v}}_1^T+{\sigma }_2{\vec{u}}_2{\vec{v}}_2^T+...+{\sigma }_r{\vec{u}}_r{\vec{v}}_r^T+0+...0$

从而$A$ 矩阵被表示为系列由${\sigma }_i{\vec{u}}_i{\vec{v}}_i^T$组成的$m\ast n$矩阵的加和的结果，奇异值$\sigma$在这里成为子矩阵$\vec{u}{\vec{v}}^T$的权重($weight$ 权值)，其中第一个${\sigma }_1$权值最大，次之${\sigma }_2$，以此类推。所以可知小奇异值对应的子矩阵对$A$矩阵的影响是很小的，舍去这些小奇异值对应的子矩阵可以做到对$A$矩阵的压缩、降噪。

3、SVD 与 PCA 降维的联系

PCA降维 主要针对协方差矩阵$X^{T}X$ 进行特征分解，找到最大的 $d$ 个特征值对应的特征向量作为基向量，对 $X$ 进行投影达到降维的目的 $X_{lowdim}=X\cdot P$。 SVD 则是针对 $X$进行奇异值分解，算的是 $X^{T}X$ 的特征值和特征向量，从求解上来说SVD与PCA等价，但是SVD 算法求解矩阵 $X^{T}X$ 的特征向量时相比暴力特征值分解有更高效的计算策略(如幂迭代法求矩阵特征值)，当找到了前 $d$ 个奇异值对应的右奇异矩阵 $V^T$，对 $X$ 进行投影达到降维的目的 $X_{lowdim}=X\cdot (V^T{)}^T$，正因如此SVD的这种高效性所，一般PCA算法常用 SVD 求解特征向量。

---

1.1 矩阵降维之矩阵分解 PCA与SVD - 知乎 (zhihu.com)
【机器学习】这次终于彻底理解了奇异值分解(SVD)原理及应用_风度78的博客-优快云博客