线性代数：线性系统求解的应用（求解矩阵的逆）

一个矩阵的逆满足条件$A\times A^{-1}=A^{-1}\times A=I$。
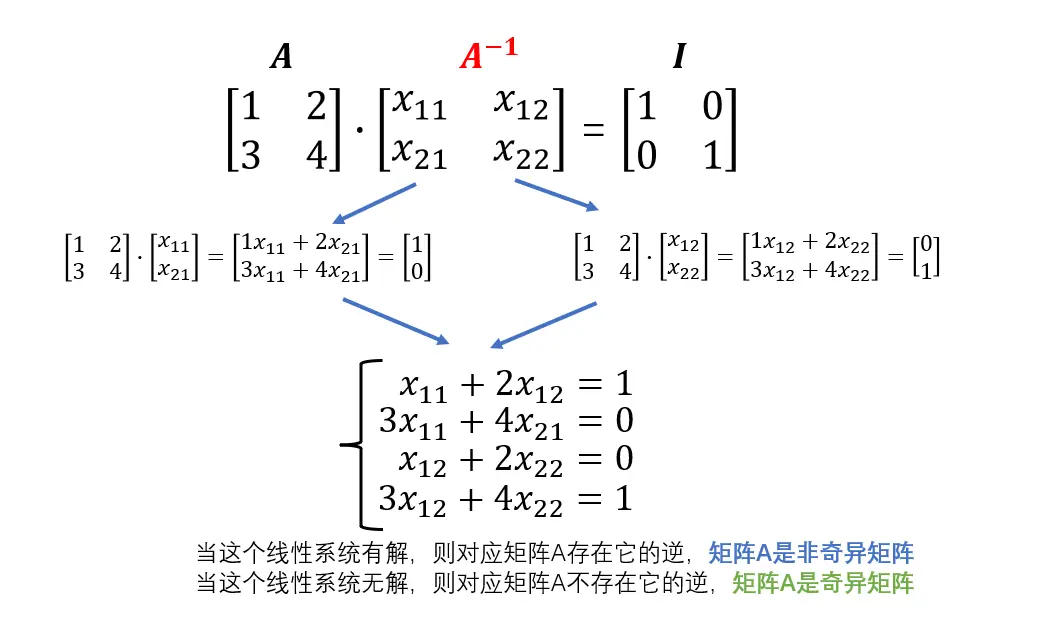
进而，求解矩阵的逆可以基于这个约束建立方程组进行处理。如求矩阵$A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$的逆$A^{-1}$可以建立如下方程组进行求解:

除了上面建立线性方程组求解，还可以通过构建更简洁的增广矩阵进行消元后直接得到矩阵的逆矩阵:
形式上为:$(\begin{array}{cc}A& I\end{array})\to (\begin{array}{cc}I& A^{-1}\end{array})$

关于增广矩阵$(\begin{array}{cc}A& I\end{array})$ 的一些细节说明:
① $(\begin{array}{cc}A& I\end{array})$构成的增广矩阵的解只有两种情况，无解和唯一解，不可能有无穷解。因为$\left[\begin{array}{ccccc}a& b& |& 1& 0\\ c& d& |& 0& 1\end{array}\right]$这种结构的 增广矩阵的右侧矩阵（结果矩阵）在通过基础变换消元过程中不可能出现全0行，而一个线性系统出现无穷解的条件就是其构成的增广矩阵的行最简形式中出现了全0行，所以对于一个方阵来说，通过构建$(\begin{array}{cc}A& I\end{array})$ 形式的增广矩阵求解逆矩阵只会出现唯一解或无解两种情况。

② 增广矩阵$(\begin{array}{cc}A& I\end{array})$ 无解的结构: $\text{增广矩阵左侧的系数矩阵存在全0行}\to \left[\begin{array}{ccccc}a& b& |& 1& 0\\ 0& 0& |& \ast & \ast \end{array}\right]$，这种情况就是方程矛盾(系数全是0，但结果不为0,不可能成立)