POJ - 3139 Balancing the Scale （状态压缩+链表）

本文探讨了一种独特的平衡天平问题，通过排列组合及状态压缩等算法手段，实现了对特定数学模型的有效求解。利用C++编程语言，设计并实现了一个能够计算不同平衡方案数量的高效算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Balancing the Scale

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 1673		Accepted: 645

Description

You are given a strange scale (see the figure below), and you are wondering how to balance this scale. After several attempts, you have discovered the way to balance it — you need to put different numbers on different squares while satisfying the following two equations:

x₁ * 4

x₂ * 3

x₃ * 2

x₄

x₅

x₆ * 2

x₇ * 3

x₈ * 4

y₁ * 4

y₂ * 3

y₃ * 2

y₄

y₅

y₆ * 2

y₇ * 3

y₈ * 4

How many ways can you balance this strange scale with the given numbers?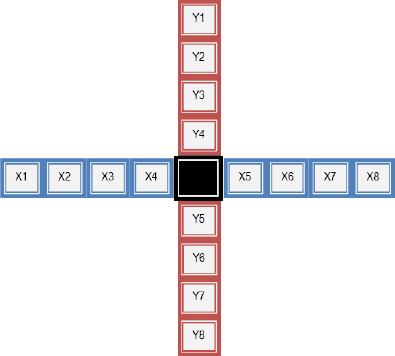

Input

There are multiple test cases in the input file. Each test case consists of 16 distinct numbers in the range [1, 1024] on one separate line. You are allowed to use each number only once.

A line with one single integer 0 indicates the end of input and should not be processed by your program.

Output

For each test case, if it is possible to balance the scale in question, output one number, the number of different ways to balance this scale, in the format as indicated in the sample output. Rotations and reversals of the same arrangement should be counted only once.

Sample Input

87 33 98 83 67 97 44 72 91 78 46 49 64 59 85 88
0

Sample Output

Case 1: 15227223

Source

Shanghai 2006

题意：

给你16个数，具体满足那个公示。

POINT：

！！16个数保证不相同，被坑了好久。

先搜索出所以C(16,4)的组合，然后A(4,4)排序。得到A(16,4)的和的种类数。可知并不大。

对每个组合得到一个sum=x1*4+x2*3+x3*2+x4*1。对每一个sum存下他的状态压缩后的数字。

然后对每一个sum(0-10240)(随便估计，比真实范围大就行)。对其中链表存下来的状压&，非0则代表数字重复。

for(i=0;i<=(1<<16)-1;i++)来计算答案就好。

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <algorithm>
#include <string.h>
using namespace std;
typedef long long  LL;
const int maxn = 50000+55;
const int maxnn= 1<<16;
int head[maxn],nxt[maxn],big[maxn];
int sz;
int a[17];
int b[5];
int num=0;
void get(int x,int now,int flag)
{
    if(x==4){
        int c[5];
        for(int i=0;i<4;i++) c[i]=b[i];
        sort(c,c+4);
        do
        {
            num++;
            int sum=0;
            for(int i=0;i<4;i++) sum+=c[i]*(4-i);
            big[sz]=flag;
            nxt[sz]=head[sum];
            head[sum]=sz++;
        }
        while(next_permutation(c, c+4));
    }
    for(int i=now+1;i<=15;i++){
        b[x]=a[i];
        get(x+1,i,flag|(1<<i));
    }
}
int main()
{
    int p=0;
    while(~scanf("%d",&a[0])&&a[0]){
        for(int i=1;i<=15;i++) scanf("%d",&a[i]);
        sz=0;
        int num[maxnn];
        memset(head,-1,sizeof(head));
        memset(num,0,sizeof num);
        get(0,-1,0);
        
        for(int i=1;i<=10240;i++){
            for(int j=head[i];j!=-1;j=nxt[j]){
                for(int k=nxt[j];k!=-1;k=nxt[k]){
                    if((big[j]&big[k])!=0) continue;
                    num[big[j]|big[k]]++;
                }
            }
        }
        LL ans=0;
        for(int i=1;i<=(1<<16)-1;i++){
            ans+=1LL*num[i]*(num[((1<<16)-1)^i]);
        }
        printf("Case %d: ",++p);
        printf("%lld\n",ans/2);
    }
    
    return 0;
}