递归算法：优雅解决复杂问题的艺术

原创于 2025-12-18 15:59:15 发布 · 557 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构 #学习 #深度优先 #leetcode

算法专栏收录该内容

6 篇文章

订阅专栏

递归算法

递归是计算机科学中最强大、最优雅的概念之一。它允许函数通过调用自身来解决复杂问题，将大问题分解为相似的小问题，直到达到可以简单解决的基本情况。无论你是算法新手还是经验丰富的开发者，深入理解递归都将极大提升你解决问题的能力。

什么是递归？

基本定义
递归是一种通过函数自身调用来解决问题的方法。一个递归函数会：

将问题分解为一个或多个相同类型的子问题
通过调用自身解决这些子问题
将子问题的解组合成原问题的解

递归的哲学
递归体现了分而治之的思想，与数学归纳法紧密相关：

如果问题在基本情况（base case）下可解
并且如果我们可以从n-1的情况推导出n的情况
那么问题对于所有n都可解

递归的三要素

基本情况（Base Case）
递归必须有一个或多个明确的终止条件，防止无限递归。
递归步骤（Recursive Step）
将原问题分解为更小的同类子问题。
向基本情况推进（Progress Toward Base Case）
每次递归调用必须使问题规模减小，最终达到基本情况。

题目：汉诺塔问题

汉诺塔2
解决汉诺塔问题是一道经典的递归问题，可为什么要用递归呢？下面手动模拟一下汉诺塔问题

移动汉诺塔：

当只有一个盘的时候，直接从a柱放到c柱即可；当有两个盘子时，需要借助b柱，将最底下往上的盘子先移到b柱，此时有一个盘子移到b柱上，然后将a柱子的盘子移到c柱，再把b柱上的盘子移到c柱上；当盘子有三个时，还是将a柱最下面往上的盘子移到b柱上；此时有两个盘子（先看成整体）要移动到b柱上，然后把a柱上的盘子移到c柱上。

此时就可以发现一个现象，当移动三层汉诺塔时，将a柱最底下往上的盘子移动到b柱后，会发现b柱出现和二层汉诺塔一样是情况，其实当汉诺塔层数为二时，移动到b柱的盘子与一层汉诺塔的情况也是一样的；所以则本题可以被解释为：

对于规模为 n 的问题，我们需要将 A 柱上的 n 个盘子移动到C柱上。
规模为 n 的问题可以被拆分为规模为 n-1 的子问题：
a. 将 A 柱上的上面 n-1 个盘移动到B柱上。
b. 将 A 柱上的最大盘移动到 C 柱上，然后将 B 柱上的 n-1 个盘移动到C柱上。
当问题的规模变为 n=1 时，即只有⼀个盘时，我们可以直接将其从 A 柱移动到 C 柱。

所以当一个大问题转化为一个相同类型的子问题；这个子问题转化为相同类型的子问题时，就可以利用递归解决问题。

至于题目的三个移动要求：
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

对于3：因为 A 中最后处理的是最大的盘子，所以在移动过程中不存在大盘子在小盘子上面的情况。
至于1：在上述模拟移动的过程中，对于a柱将多个盘子视为一体移动到b柱子上这个过程在实际的递归移动过程中，确实是只移动了一个盘子，后续会画递归展开图详细剖析，以验证递归确实是行得通的。

以下是示意图，当层数为4时也是与上述说法一致；所以解决汉诺塔一共有如下三个步骤

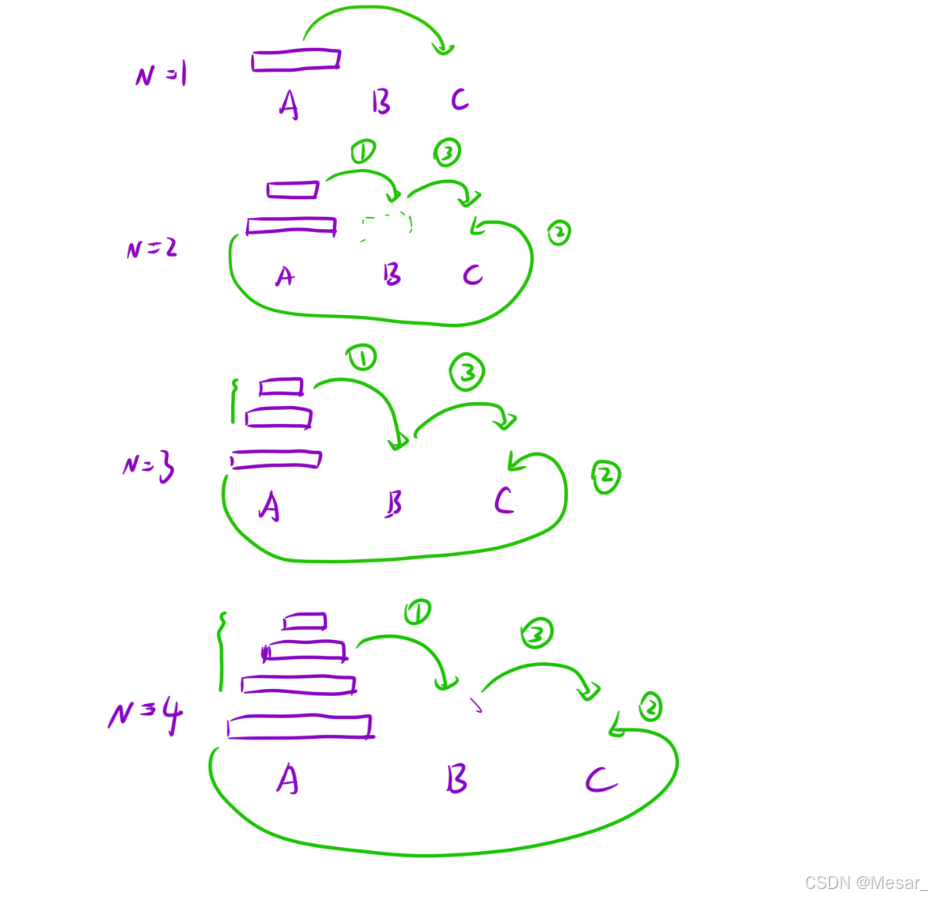
对于递归函数的书写，主张三个原则：

研究相同子问题——函数头的设计；以汉诺塔为例：a柱上的盘子需要借助b柱移动到c柱上；所以函数头也就设计出来了：需要三个柱子，而且当层数不一样时，操作也有所不同

void dfs(vector<int>&a,vector<int>&b,vector<int>&c,int n)//研究相同子问题（函数头）

解决相同子问题——函数体的书写；结合上述移动示意图的三个步骤：1)当层数大于1时，都需要将a柱的最大盘往上的盘移动到b柱上；2)将a柱的最大盘移动到c柱上；3)将b柱上的盘子移动到c柱上；其中这里的1，3都是子问题，都需要进行递归，但是在书写时，不要尝试把它展开，不要把它展开，不要把它展开！你只需要相信这个递归函数一定能够解决问题即可
递归出口；函数不能一直递归下去，否则会栈溢出；所以当层数为1时就是出口

代码实现

class Solution 
{
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) 
    {
        dfs(A,B,C,A.size());
    }
    void dfs(vector<int>&a,vector<int>&b,vector<int>&c,int n)//研究相同子问题（函数头）
    {
        //*
        if(n==1)//函数出口
        {
            c.push_back(a.back());
            a.pop_back();
            return;
        }
        //只关心如何解决一个子问题
        //步骤1
        dfs(a,c,b,n-1);
        //步骤2
        c.push_back(a.back());
        a.pop_back();
        //步骤3
        dfs(b,a,c,n-1);
    }
};

为了验证一下，递归函数这个黑盒是否真的能解决问题，我们尝试将其展开，以三层的为例；
这里要抓住几个重点；

明确你当前是在那个函数体中，这样你的操作才对的上。
函数里的abc代表的是对应函数形参的左中右位置的参数（a-左，b-中，c-右）
展开图里的原abc指的是abc柱；

        //*
        if(n==1)//函数出口
        {
            c.push_back(a.back());
            a.pop_back();
            return;
        }
        //只关心如何解决一个子问题
        //步骤1
        dfs(a,c,b,n-1);
        //步骤2
        c.push_back(a.back());
        a.pop_back();
        //步骤3
        dfs(b,a,c,n-1);

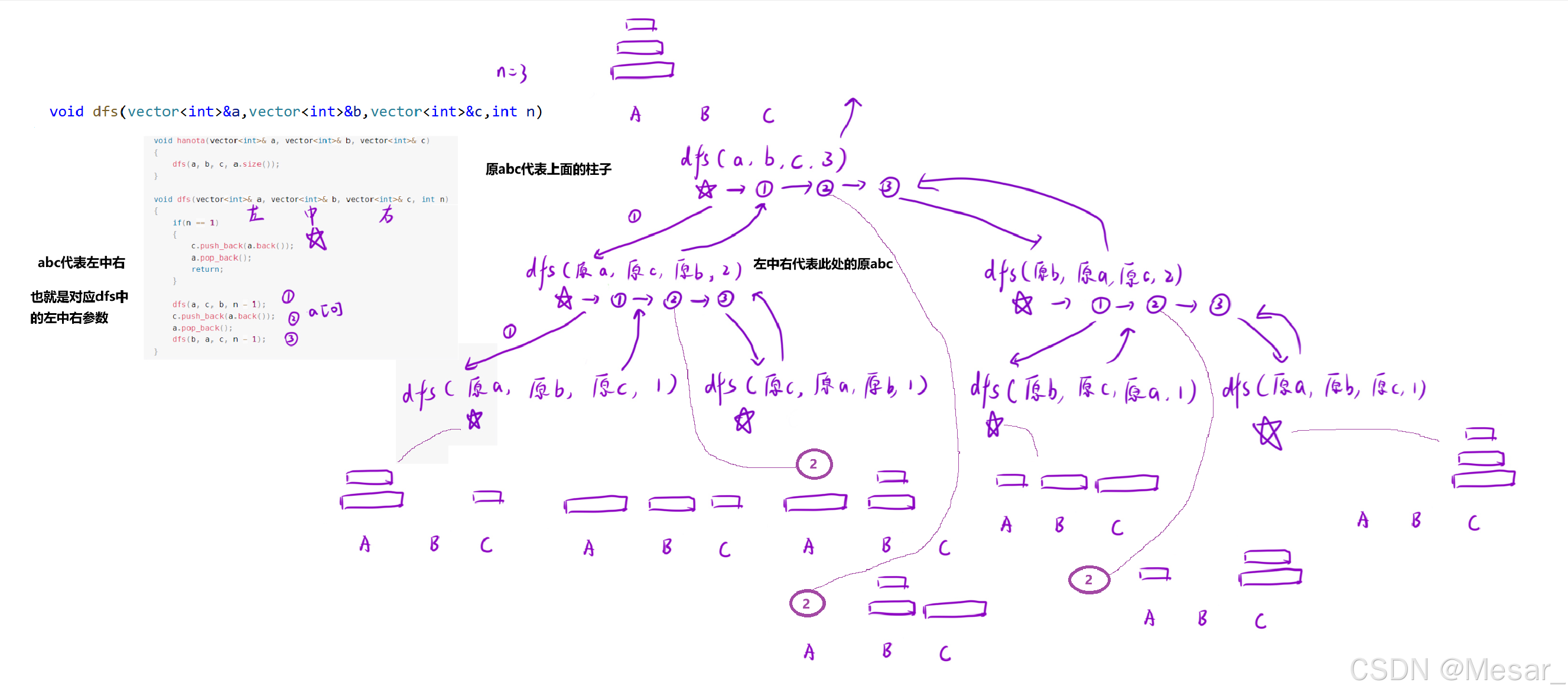
汉诺塔展开图
以最左分支部分为例：当的调用dfs后，执行步骤1代码dfs(a,c,b,n-1);：将a柱往上的盘子移到b柱上；所以对应的递归展开为dfs(原a，原c，原b，2)，在dfs(原a，原c，原b，2)这个函数中执行步骤1 dfs(a,c,b,n-1);，又是子问题，所以继续递归展开为dfs(原a，原b，原c，1)，在dfs(原a，原b，原c，1)中，n=1，满足出口条件，所以此时将a柱最上面一块移到c柱上；如图所示；在递归展开图中下一层递归函数的三个参数是原a，原b，原c时要结合执行的代码来看，将代码中的abc（左中右）对照函数体的参数；剩余的就看图自行推断吧；所以，在日常写递归函数体时就不要不要想着把它展开，而是相信这个递归函数一定能做到。

题目：翻转链表

翻转链表
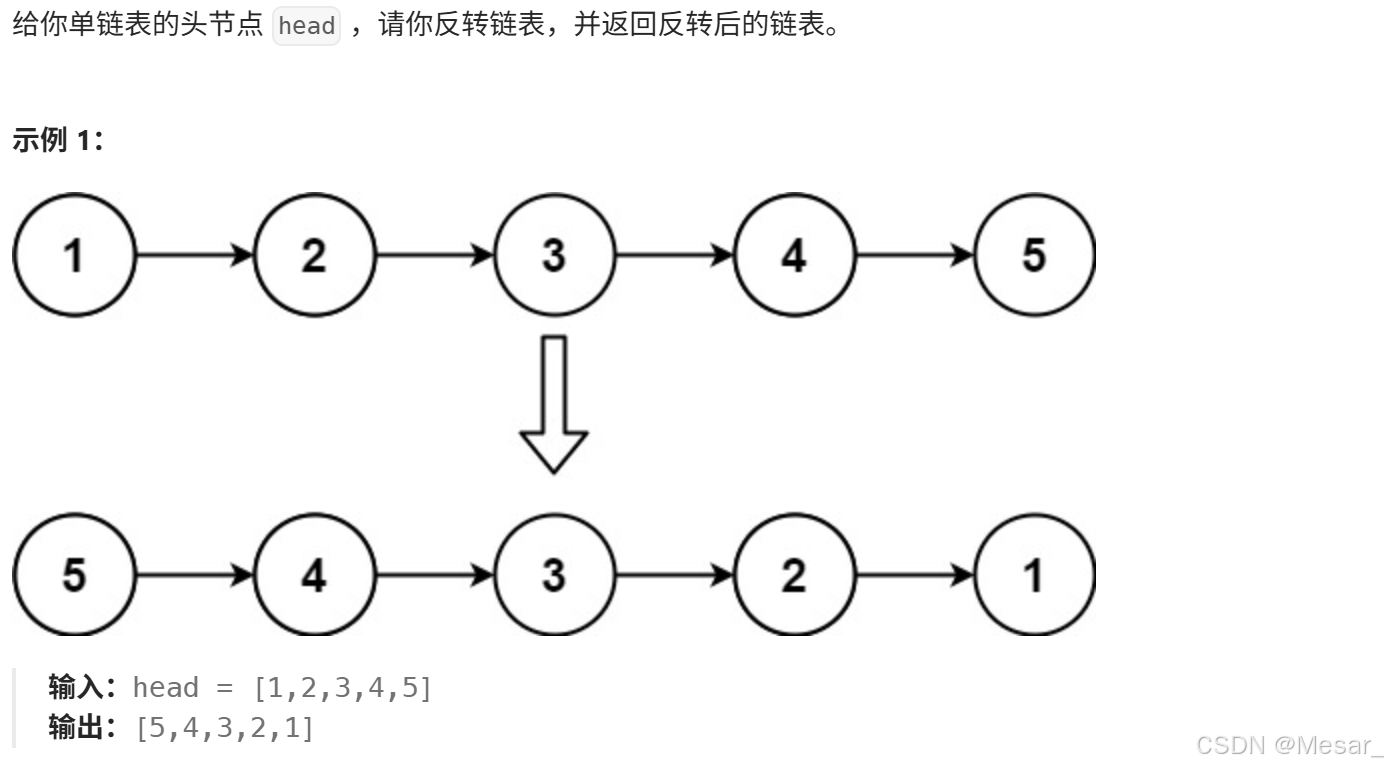
这道题想必也不陌生了，之前使用迭代的方式进行反转链表；今天以递归的视角看待这道题；

递归不单单只能解决树类型的题目；对于那些含有相同子问题的题目依旧可以使用递归解决；
算法思路：

找相同的子问题：交给你⼀个链表的头指针，逆序之后，返回逆序后的头结点；由此就可以设计出递归函数头
解决这个相同的子问题：先把当前结点之后的链表逆序，逆序完之后，把当前结点添加到逆序后的链表后面即可；
递归出口：当前结点为空或者当前只有⼀个结点的时候，不用逆序，直接返回。

翻转链表

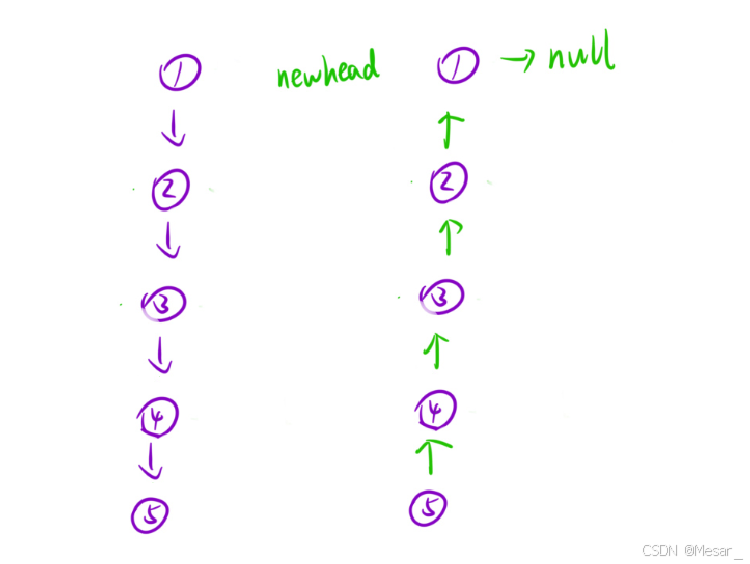
代码实现：

class Solution 
{
public:
    ListNode* reverseList(ListNode* head) 
    {
        if(head==nullptr)return head;//head为空的情况

        if(head->next==nullptr) return head;//新的头节点

        ListNode* newhead=reverseList(head->next);
        head->next->next=head;
        head->next=nullptr;//翻转最后一个时（原来的头节点）将其变成尾节点
        return newhead;//返回新的头节点
        
    }
};

题目：合并两个有序链表

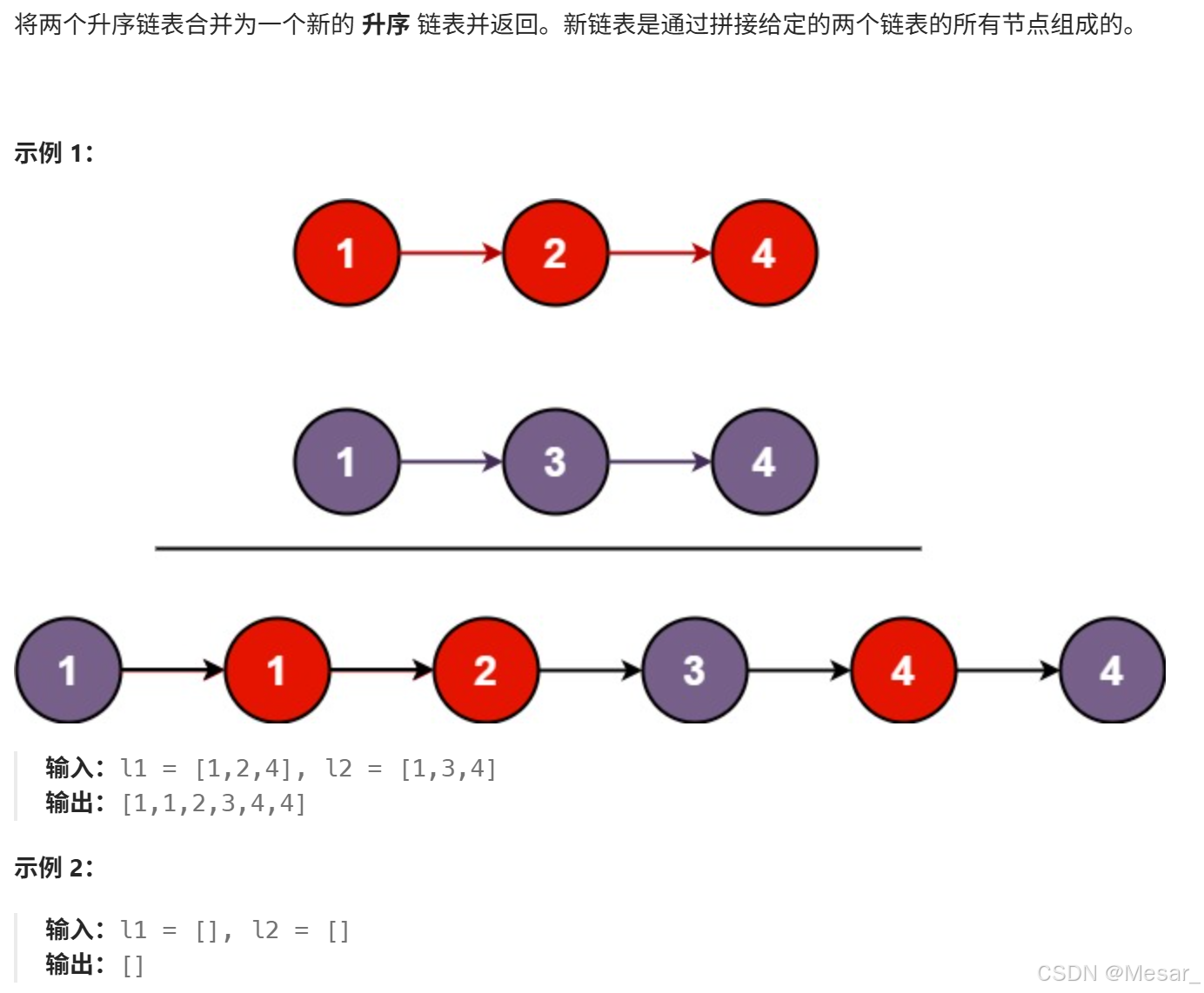
合并两个有序链表

算法思路：

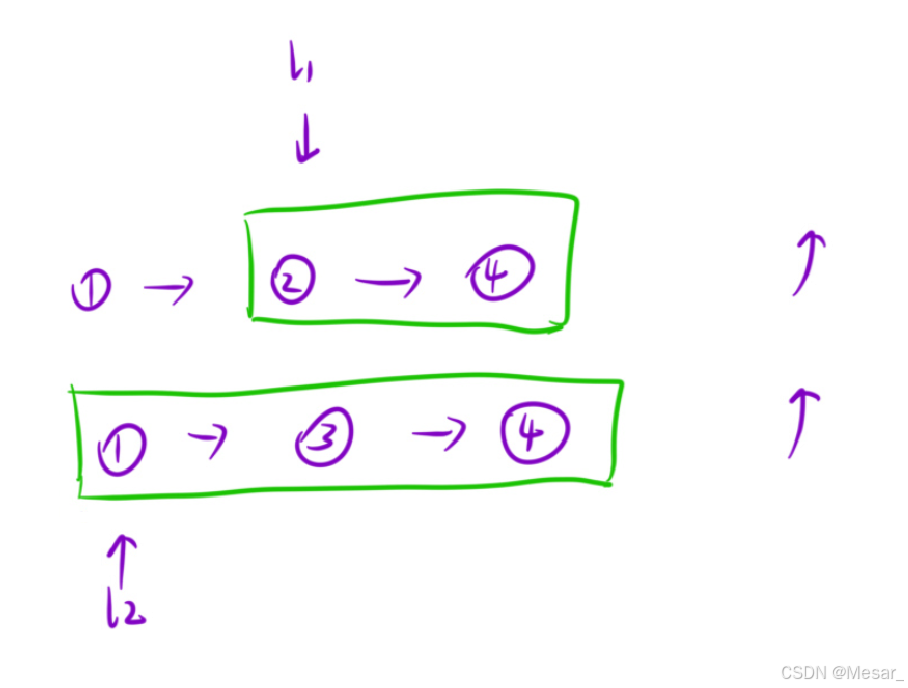
寻找相同子问题：交给你两个链表的头结点，你帮我把它们合并起来，并且返回合并后的头结点；
解决相同子问题：选择两个头结点中较小的结点作为最终合并后的头结点，然后将剩下的链表交给递归函数去处理；
递归出口：当某⼀个链表为空的时候，返回另外⼀个链表。

合并两个有序链表

代码实现

class Solution 
{
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) 
    {
        if(l1==nullptr)return l2;
        if(l2==nullptr)return l1;

        if(l1->val<=l2->val)
        {
            l1->next=mergeTwoLists(l1->next,l2);
            return l1;//返回新的头节点
        }
        else
        {
            l2->next=mergeTwoLists(l1,l2->next);
            return l2;//返回新的头节点
        }
        
    }
};

题目：两两交换链表中的节点

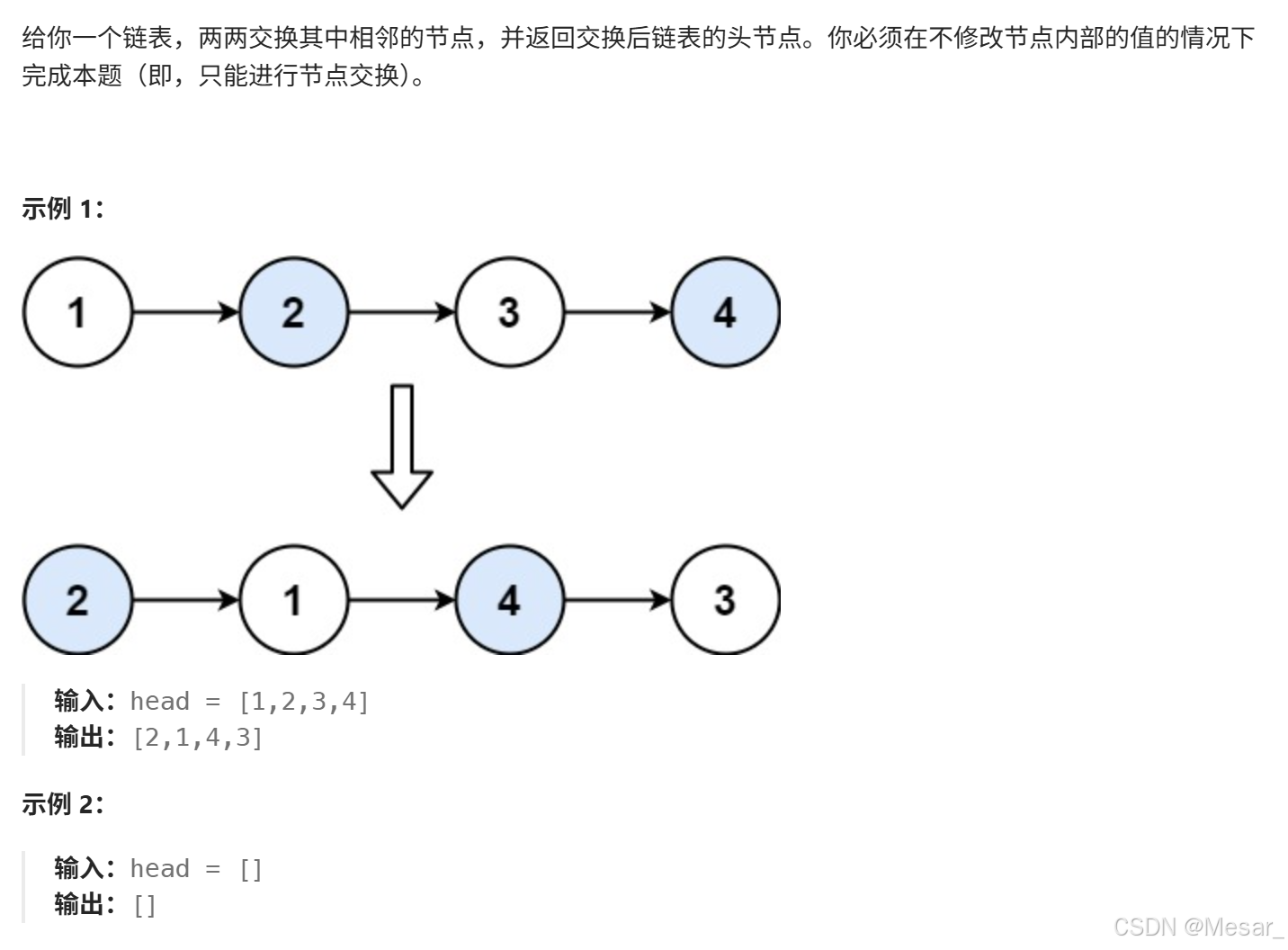
两两交换节点
算法思路：

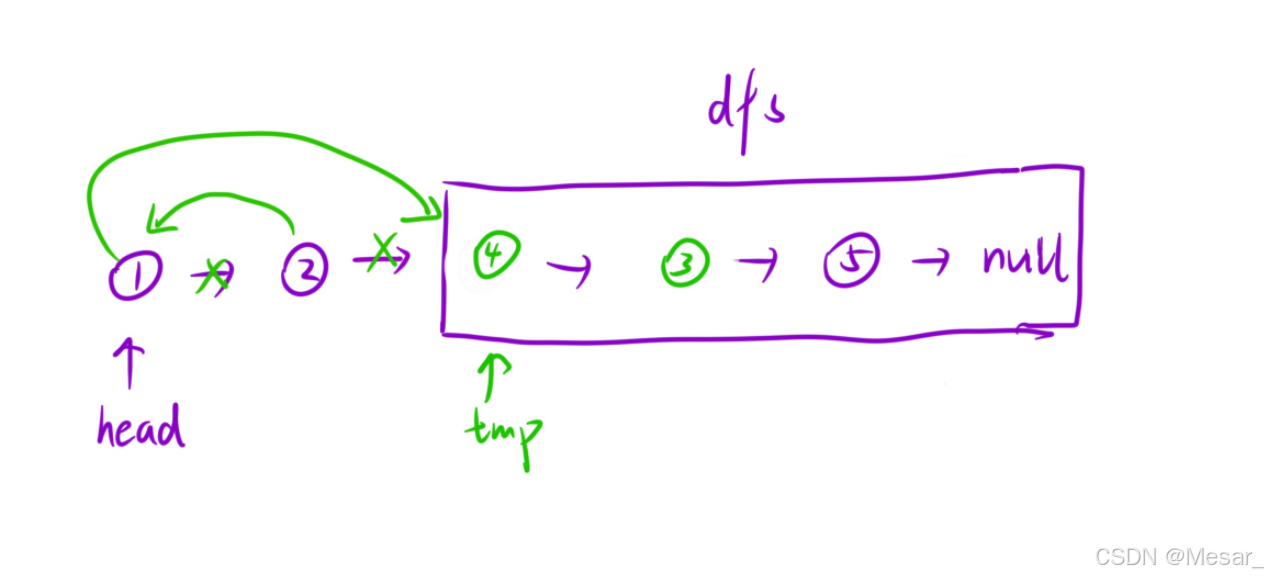
寻找相同子问题：交给你⼀个链表，将这个链表两两交换⼀下，然后返回交换后新的头结点；
解决相同子问题：先去处理⼀下第⼆个结点往后的链表，然后再把当前的两个结点交换⼀下，连接上后面处理后的链表；
递归出口：当前结点为空或者当前只有⼀个结点的时候，不用交换，直接返回。

两两交换

代码实现

class Solution 
{
public:
    ListNode* swapPairs(ListNode* head) 
    {
        if(head==nullptr||head->next==nullptr)return head;//空或者只剩一个节点的情况

        ListNode*ret=head->next;//先保存当前头节点的下一节点（也是新的头节点）
        head->next=swapPairs(head->next->next);//当前头节点连接翻转好的链表
        ret->next=head;//逆置当前的两个节点
        
        return ret;//返回新的头节点
    }
};

题目：Pow(x,n)

求快速幂

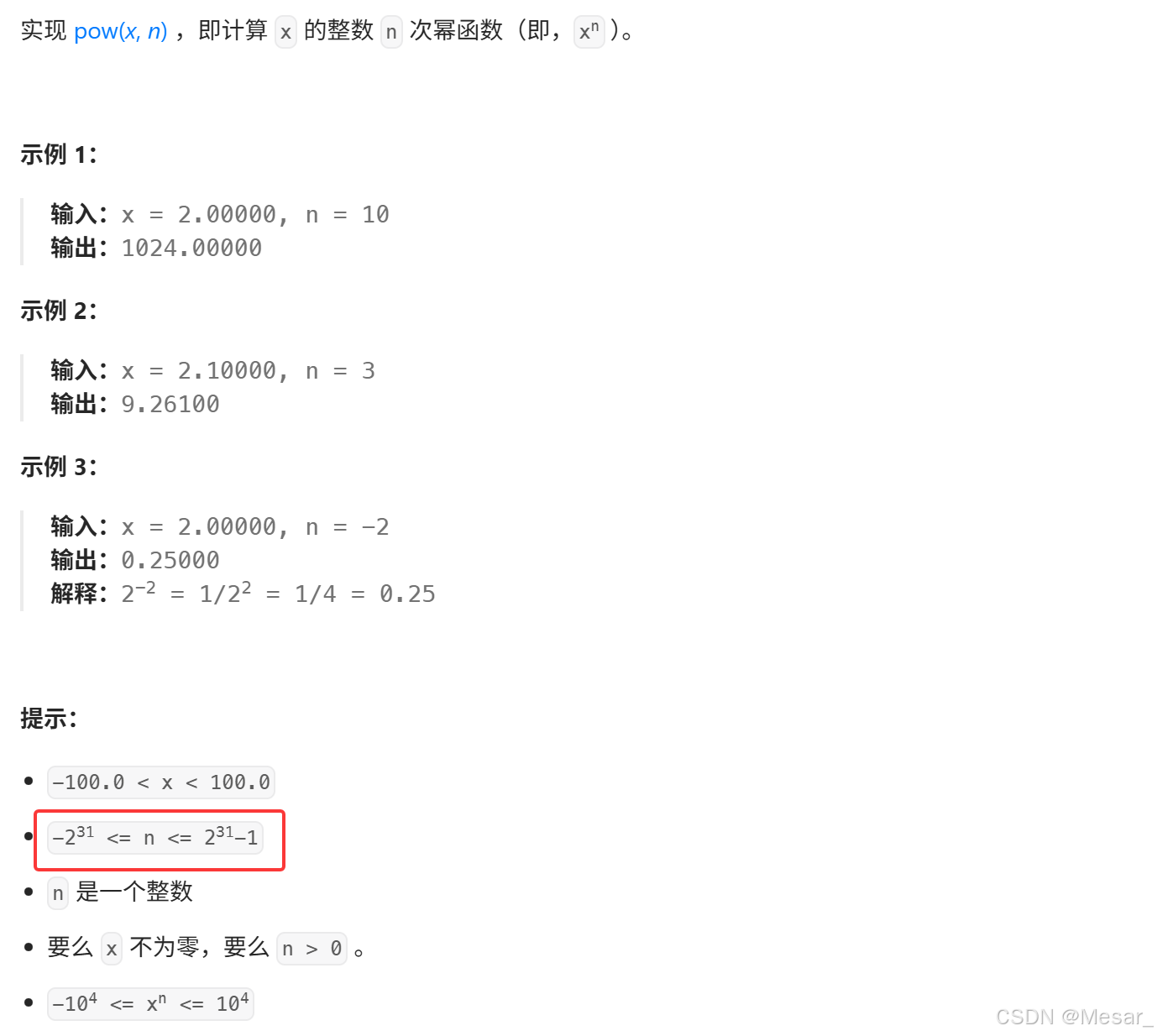
这里提供一种求快速幂解法，时间复杂度为 $O (l o g N)$

快速幂

算法思路：

寻找相同子问题：求出 x 的 n 次方是多少，然后返回；
解决相同子问题：先求出 x 的 n / 2 次方是多少，然后根据 n 的奇偶，得出 x 的 n 次方是多少；
递归出口：当 n 为 0 的时候，返回 1 即可。

class Solution 
{
public:
    double myPow(double x, int n) 
    {
        //n可以为负数，判断转换处理一下
        return n<0?1.0/Pow(x,-(long long )n):Pow(x,n);
        
    }

    double Pow(double x, long long n) 
    {
        if(n==0)return 1.0;//出口

        double tmp=Pow(x,n/2);//递归处理
        
        return n%2==0?tmp*tmp:tmp*tmp*x;
    }
};

注意：由于指数n可以为负数，所以当n为负数时可以将其转化为正数得： $1.0/ P o w (x, - (l o n g l o n g) n)$ ，而指数 $n = -2^{31}$ ，转化为正数时，int存不下，所以使用long long

总结

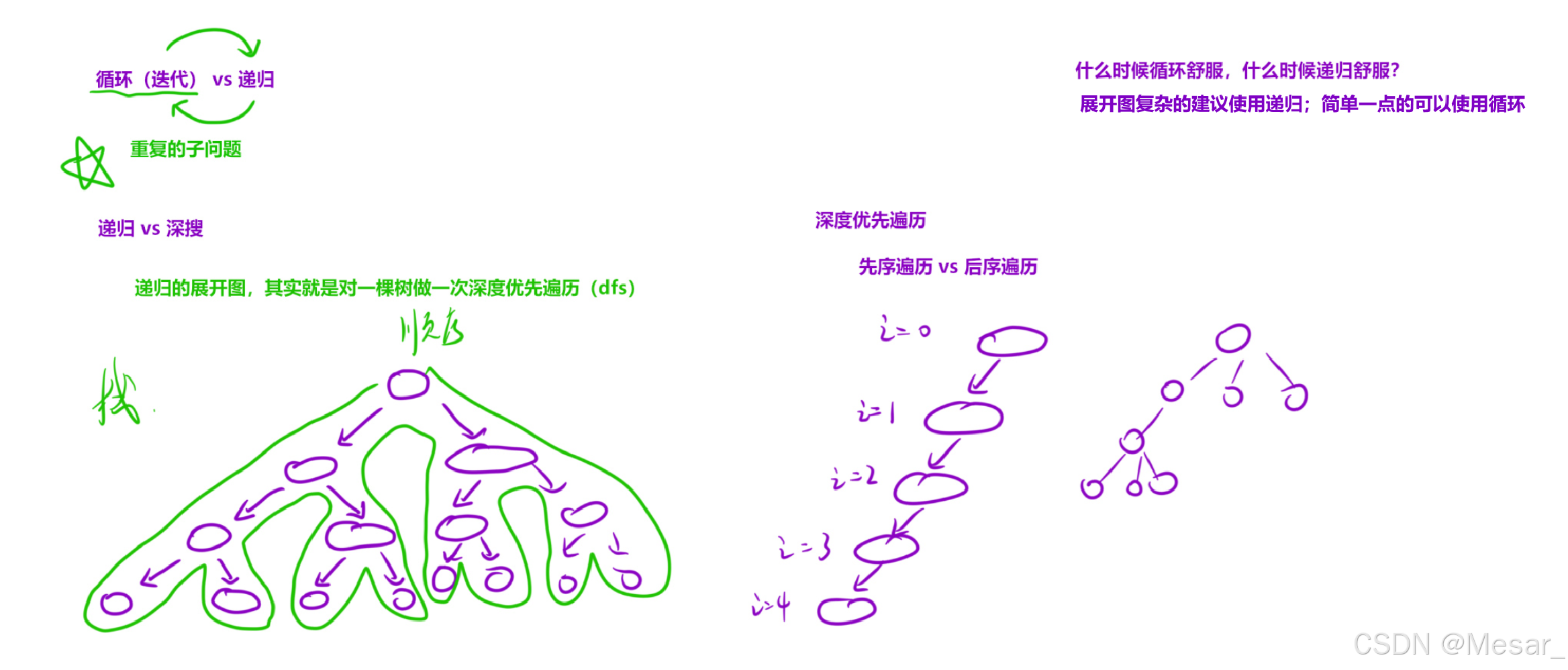
以上题目使用循环（迭代）或者递归都是可以解决问题的；两者是可以转换实现的，就类似二叉树的遍历时利用了栈来实现循环访问；而循环和递归处理问题的时序一般是不一样的，一般来说循环从前往后；递归从后往前（后序遍历）在处理上述链表的题型时，可以将链表看成单叉树，从这个角度看会不会好理解一点呢？于是就可以对这个单叉树进行深度优先遍历处理相同子问题了。