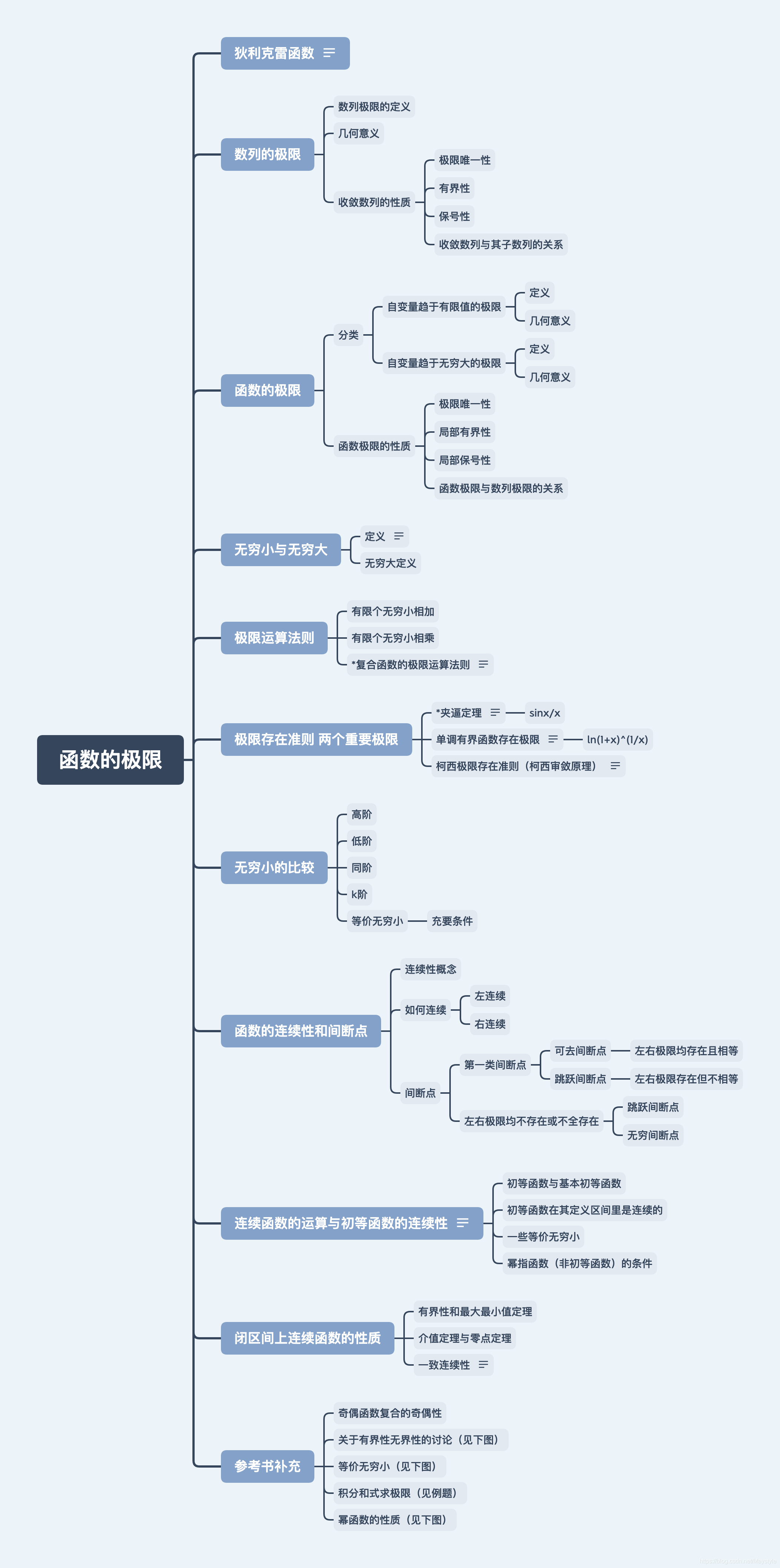

有界无界的讨论:

等价无穷小与佩亚诺余项:



洛必达法则成立条件:



佩亚诺余项:


要学会观察:


n项和或n项因式积的数列的极限:

以递推形式给出数列的极限:

以极限形式定义的函数表达式:

复合函数的极限:



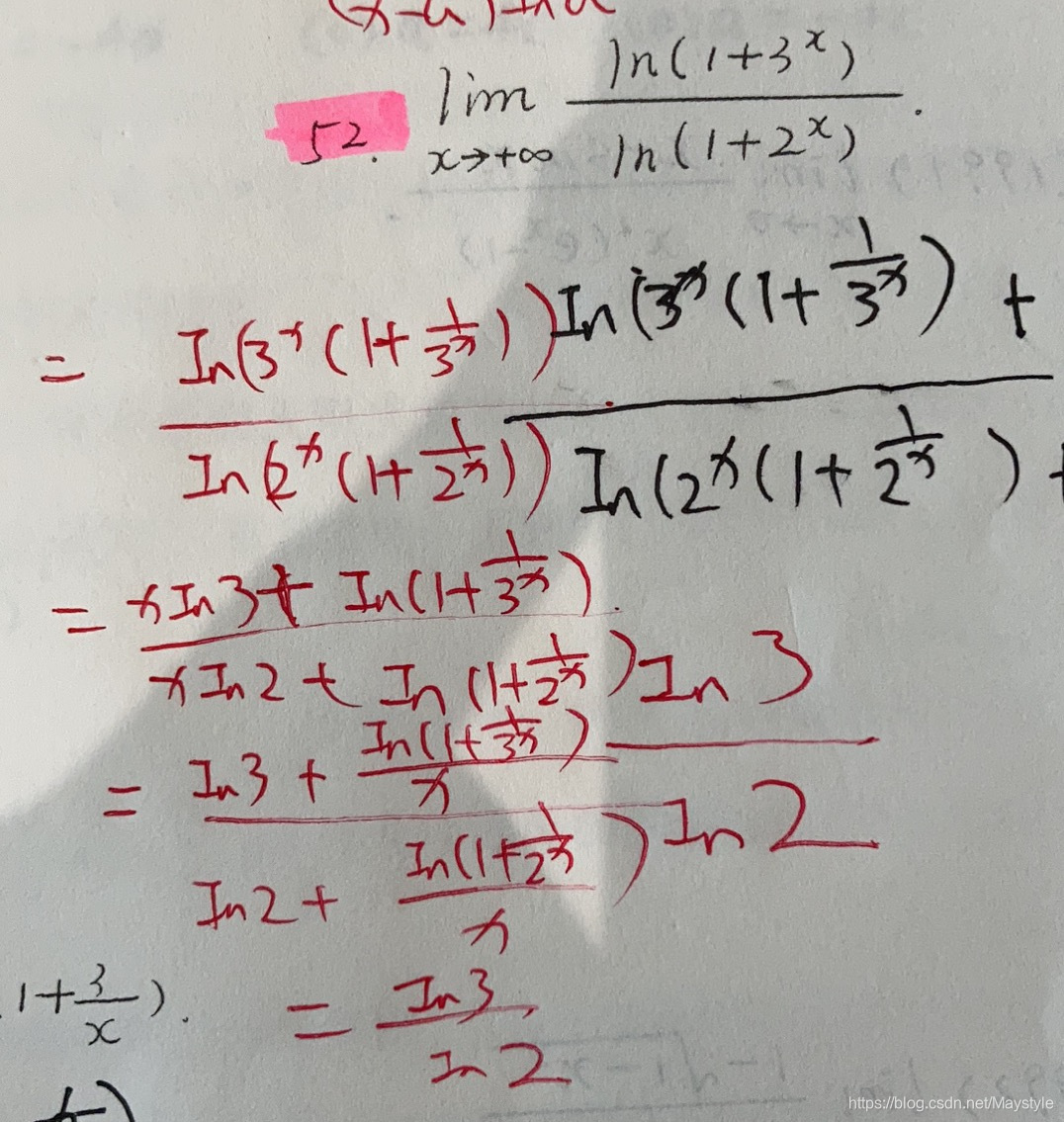
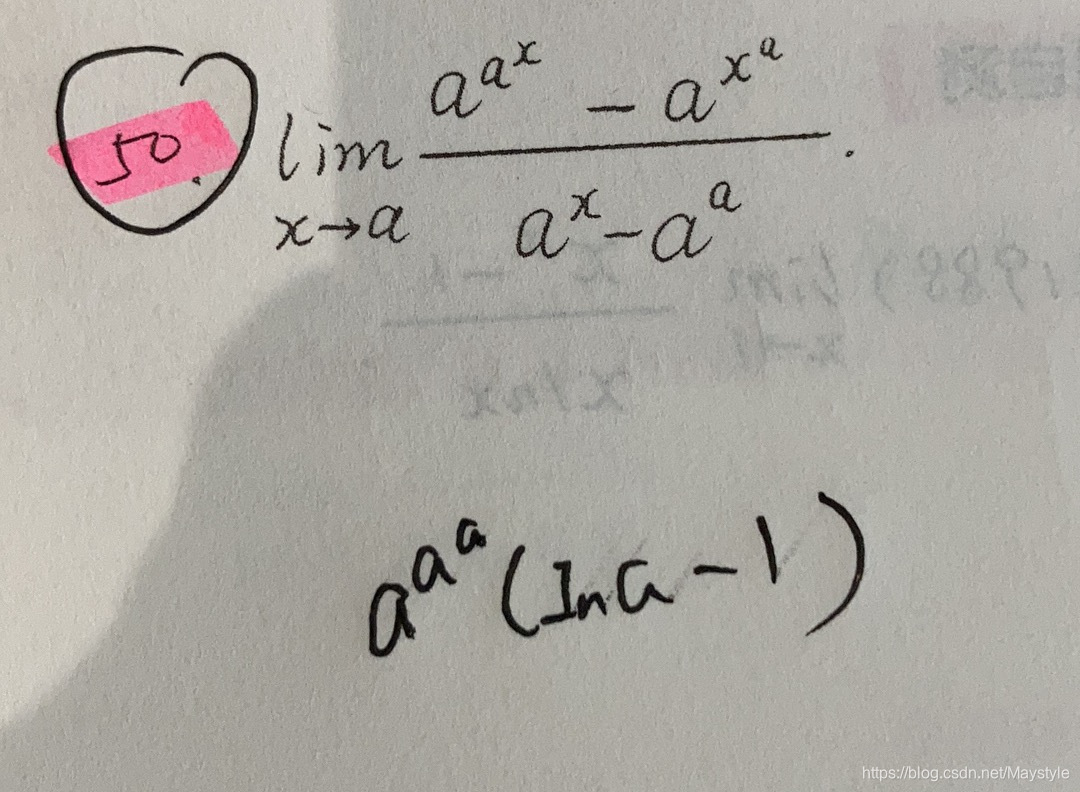

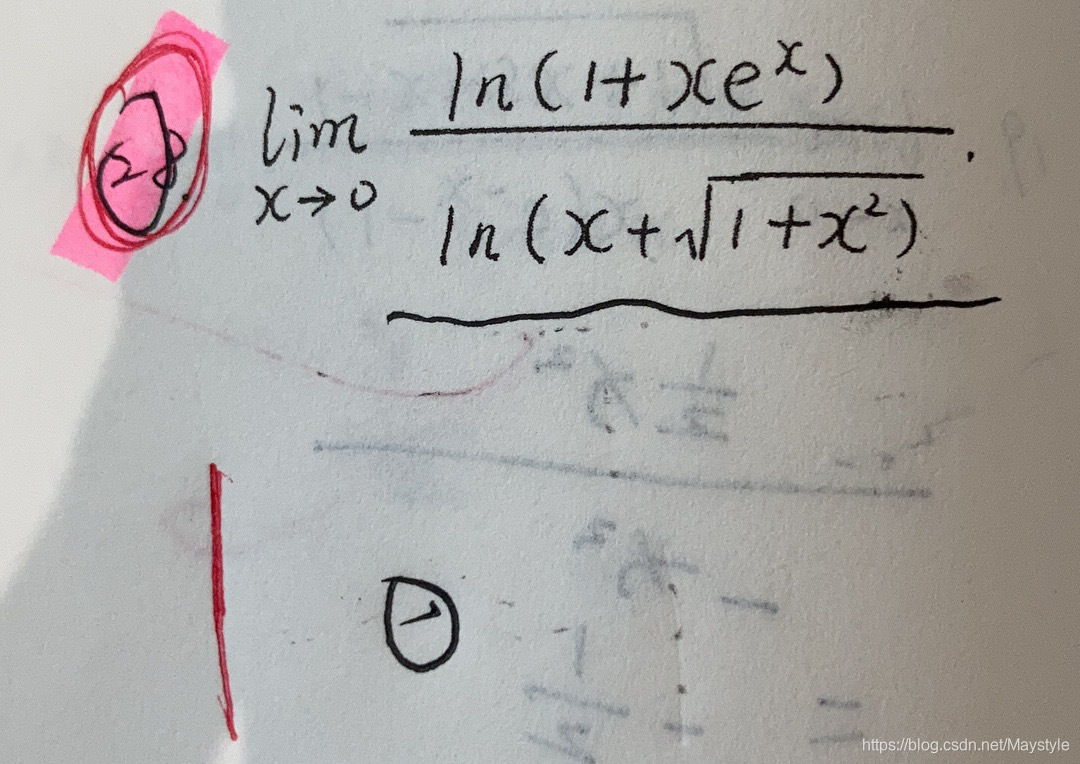
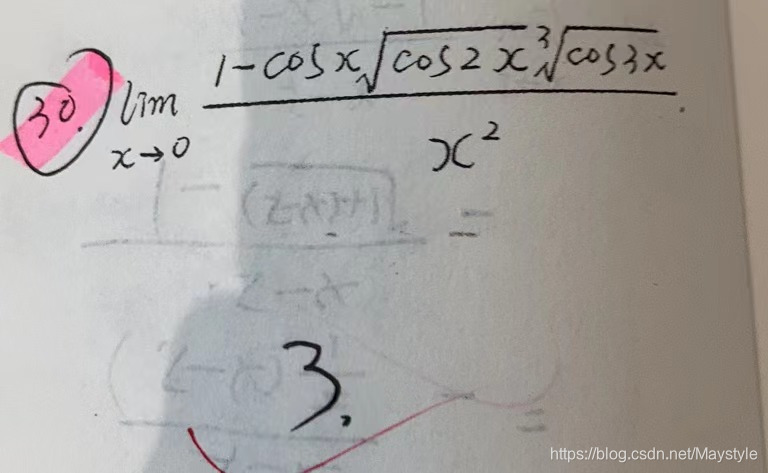
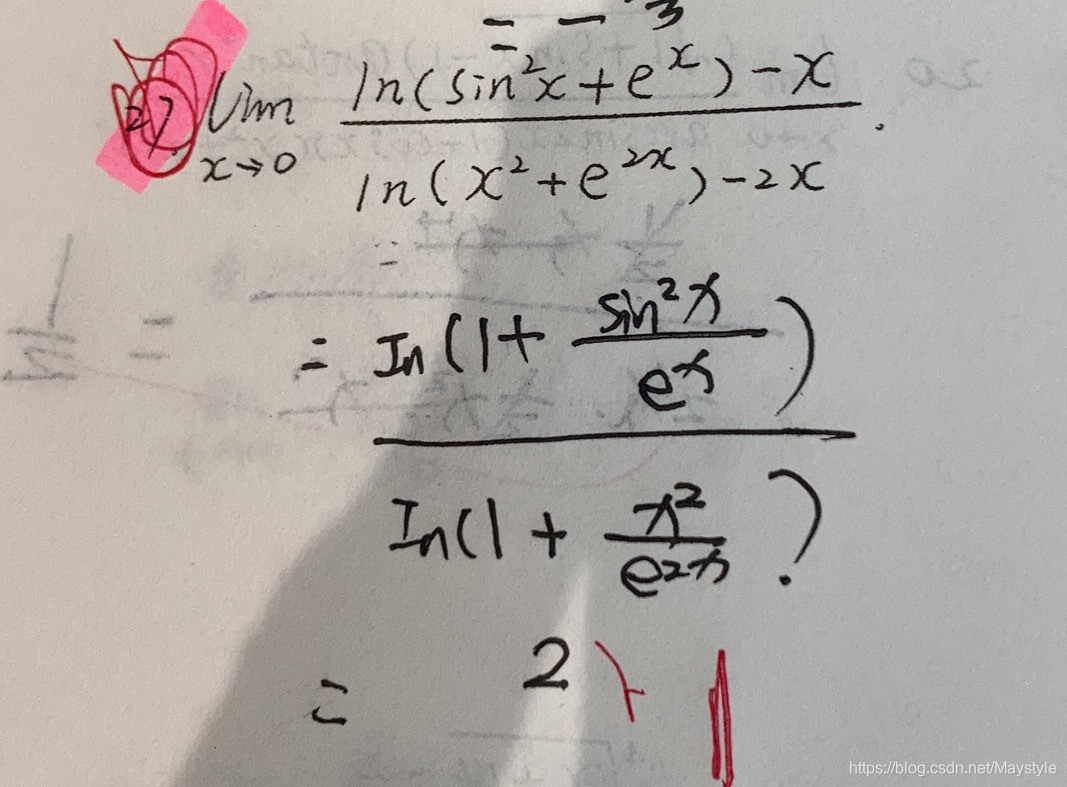
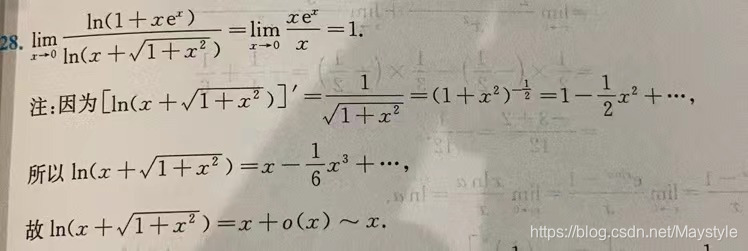
极限的同号性

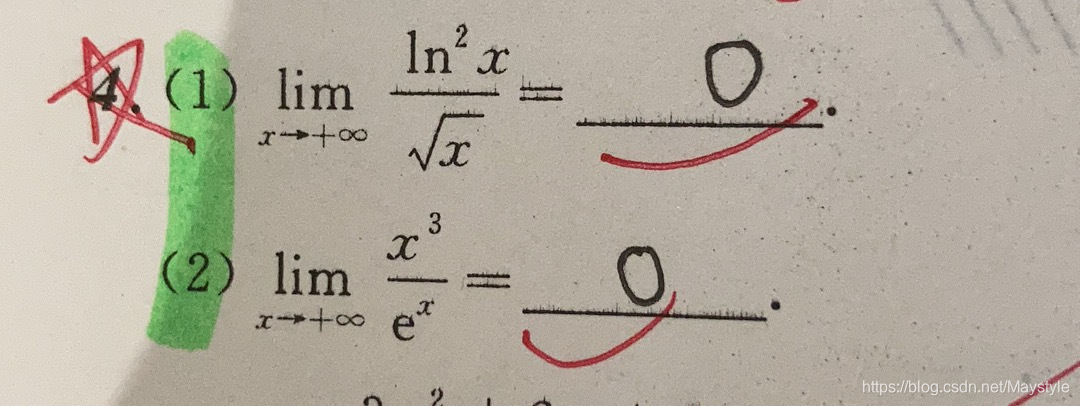


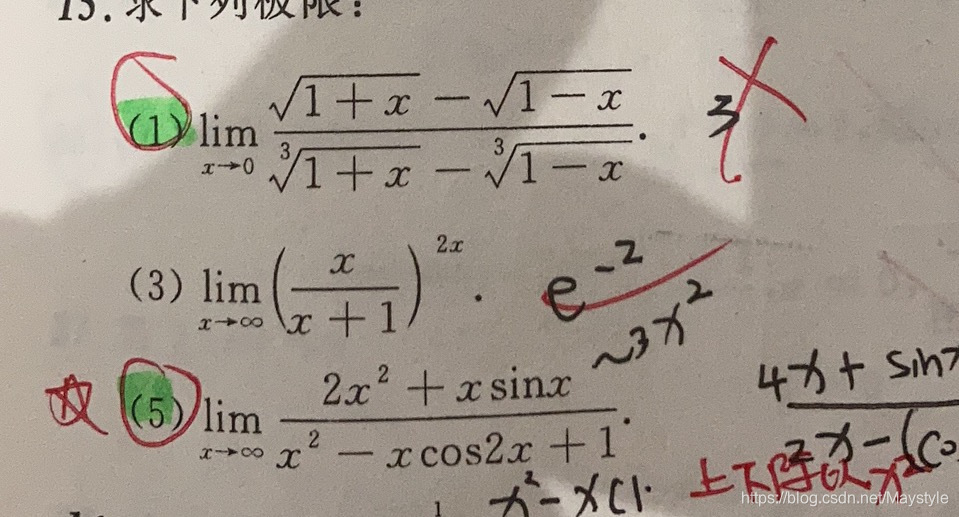
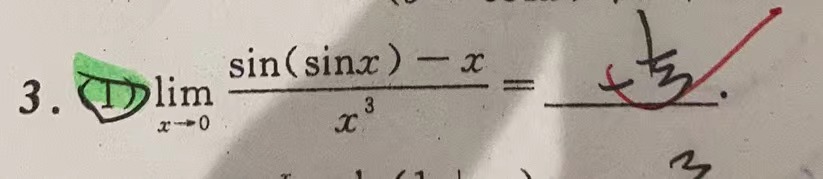
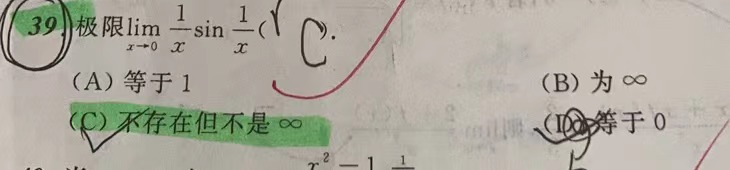


 这篇博客探讨了数学分析中的关键概念,包括等价无穷小、洛必达法则的成立条件以及佩亚诺余项在求解极限问题中的应用。博主强调了在处理n项和或n项因式积的数列极限时的观察技巧,并通过递推形式和极限定义解释了如何理解函数表达式的极限。同时,还涉及了复合函数的极限计算及其同号性原理。
这篇博客探讨了数学分析中的关键概念,包括等价无穷小、洛必达法则的成立条件以及佩亚诺余项在求解极限问题中的应用。博主强调了在处理n项和或n项因式积的数列极限时的观察技巧,并通过递推形式和极限定义解释了如何理解函数表达式的极限。同时,还涉及了复合函数的极限计算及其同号性原理。


有界无界的讨论:

等价无穷小与佩亚诺余项:



洛必达法则成立条件:



佩亚诺余项:


要学会观察:


n项和或n项因式积的数列的极限:

以递推形式给出数列的极限:

以极限形式定义的函数表达式:

复合函数的极限:



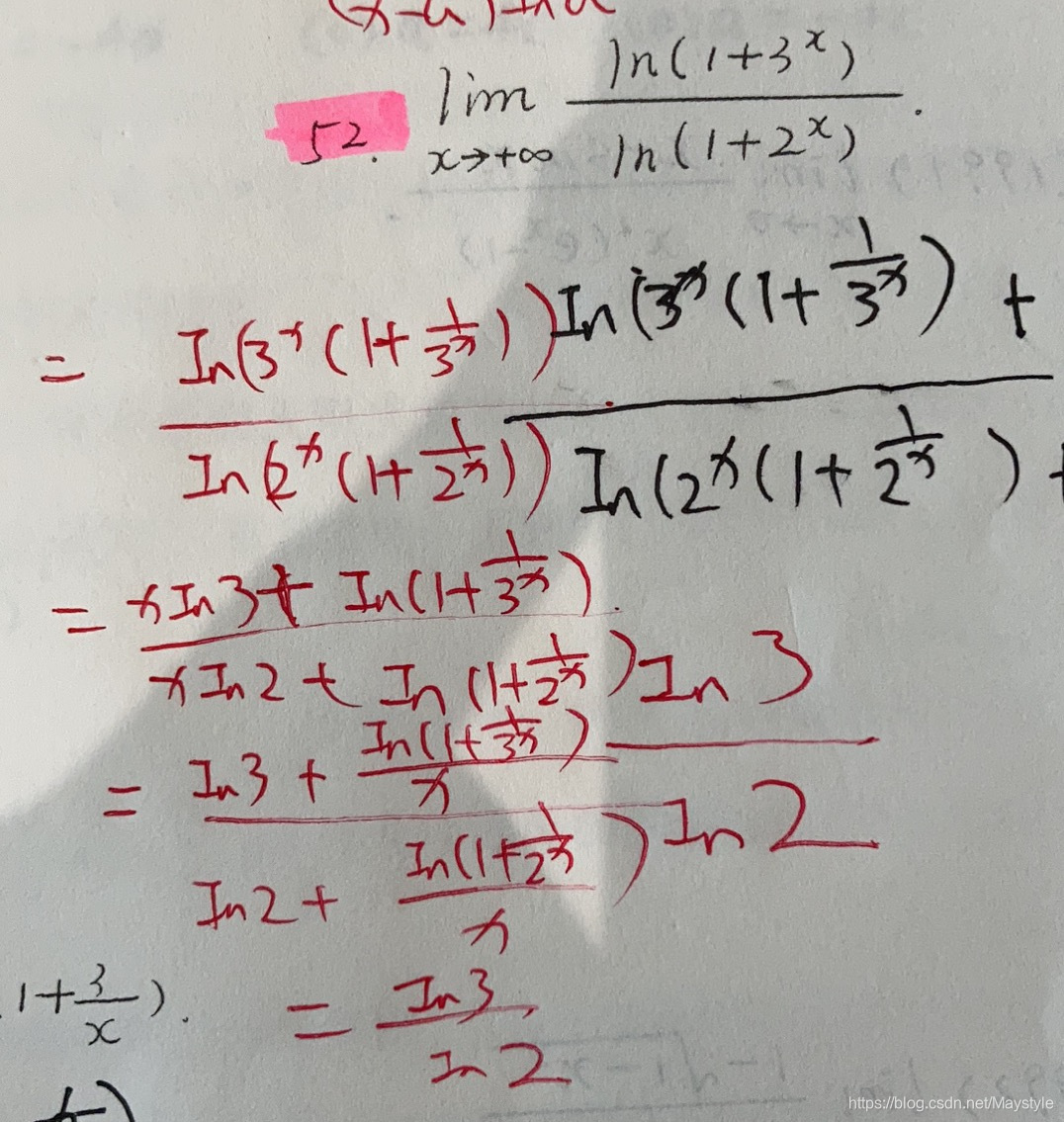
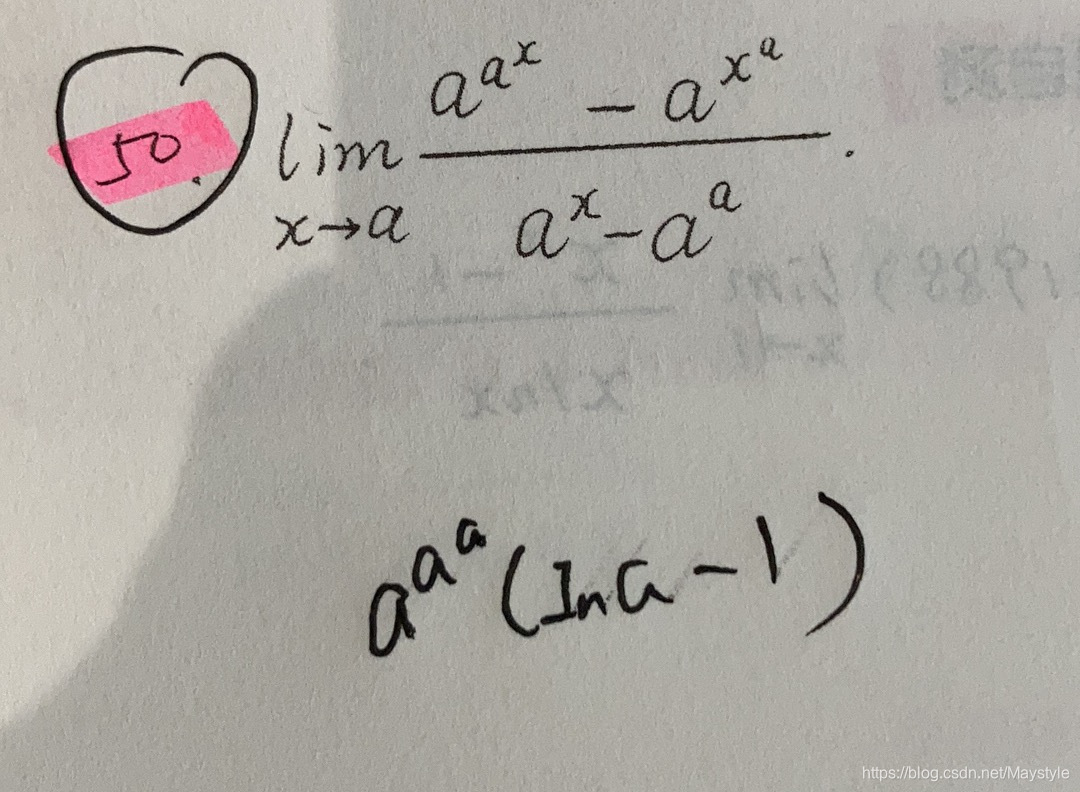

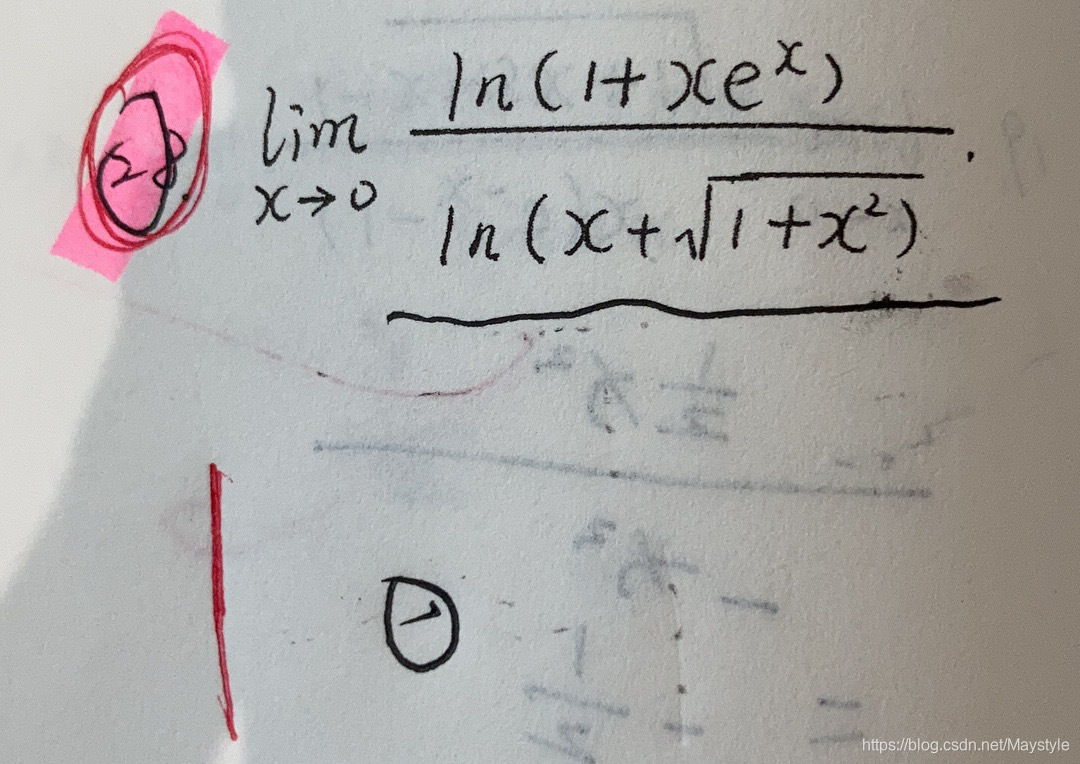
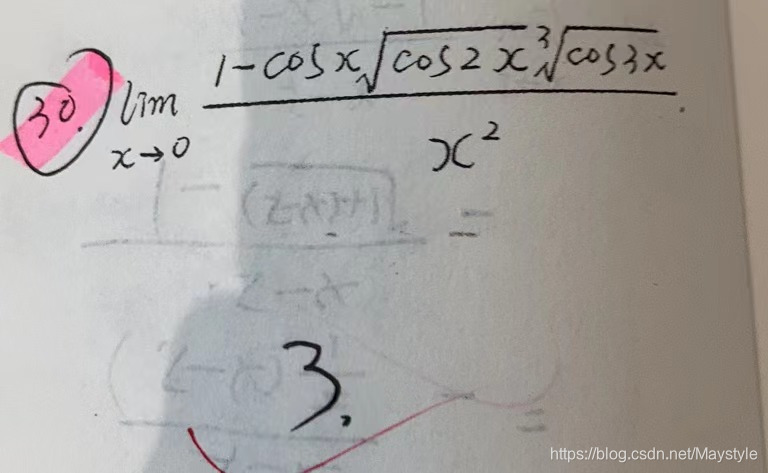
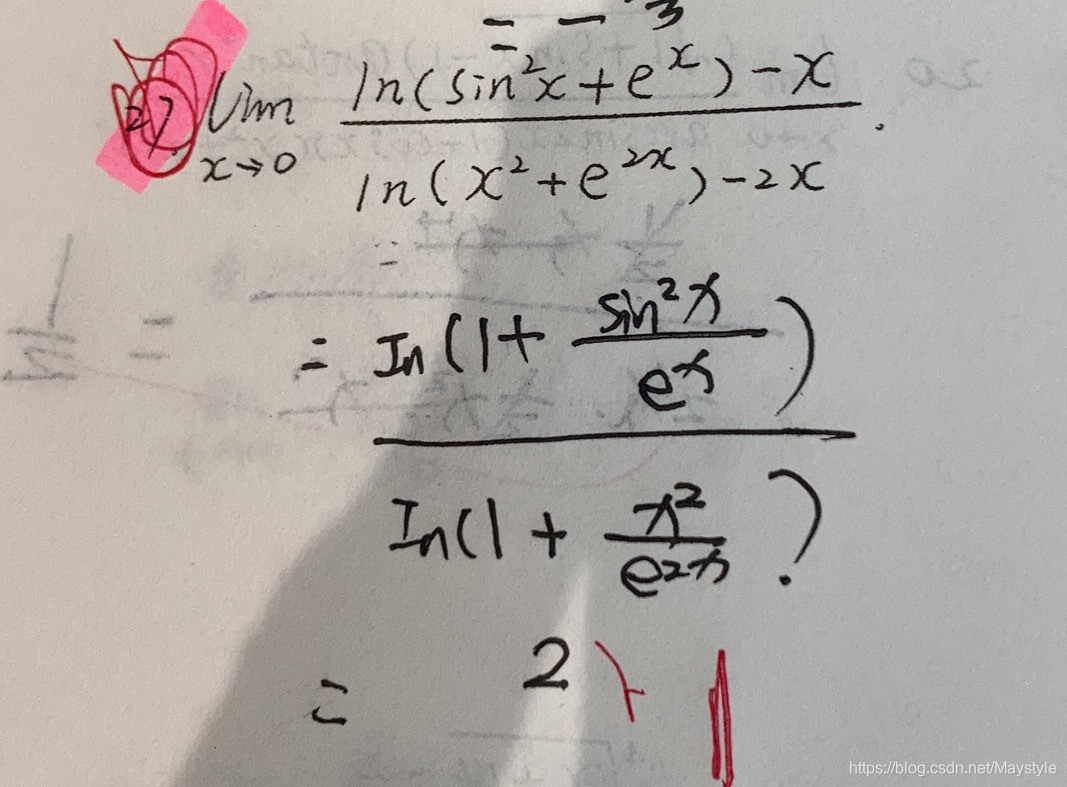
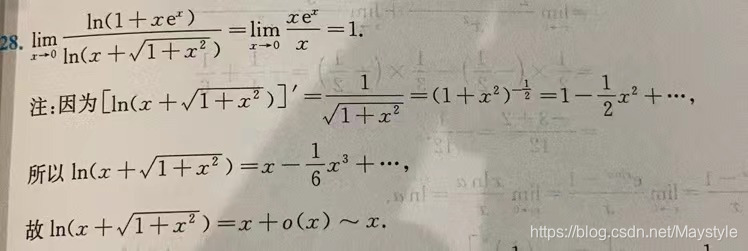
极限的同号性



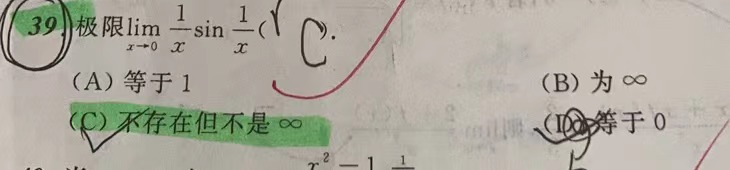


 440
440
 265
265

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


