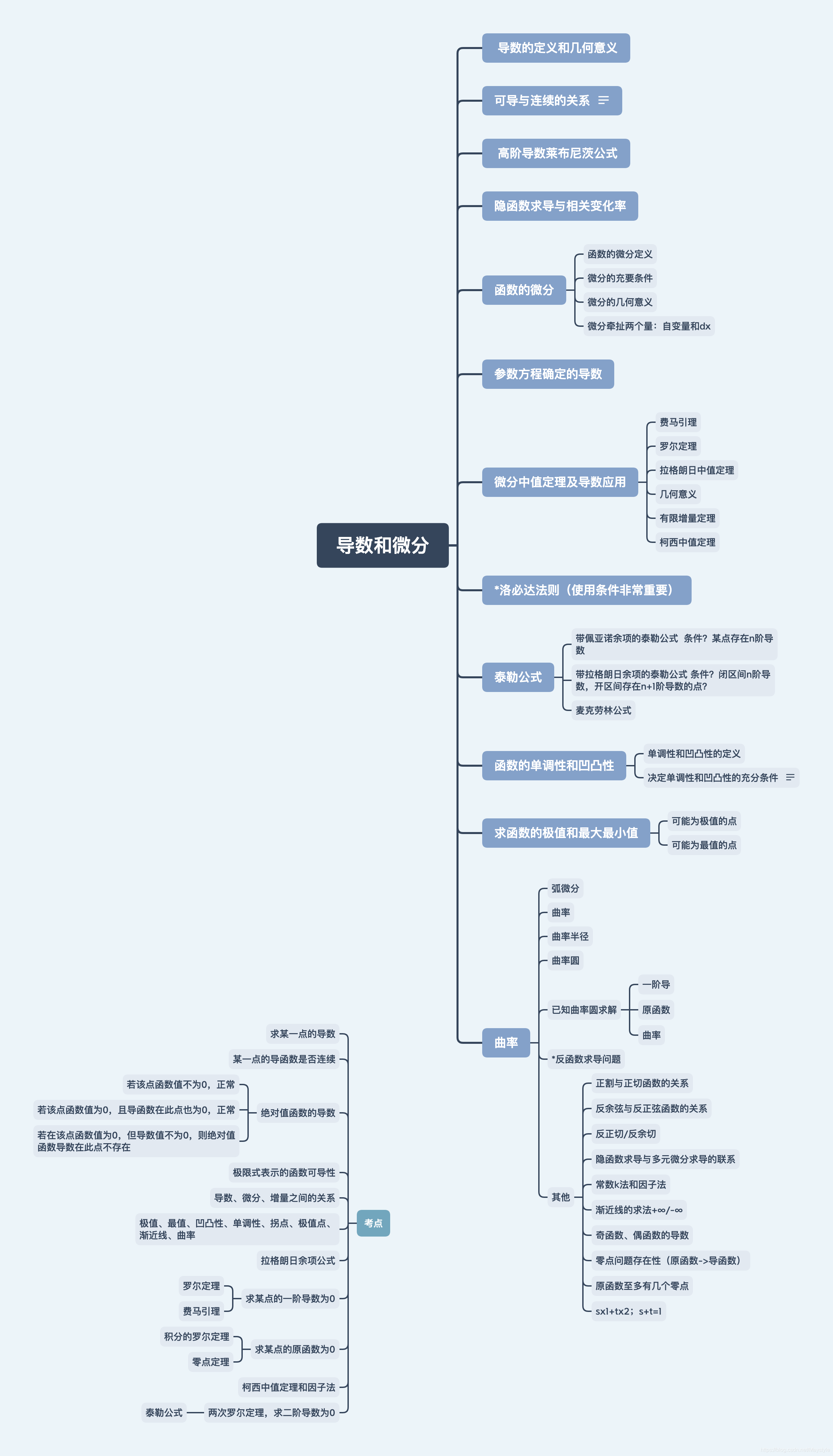
莱布尼茨公式:
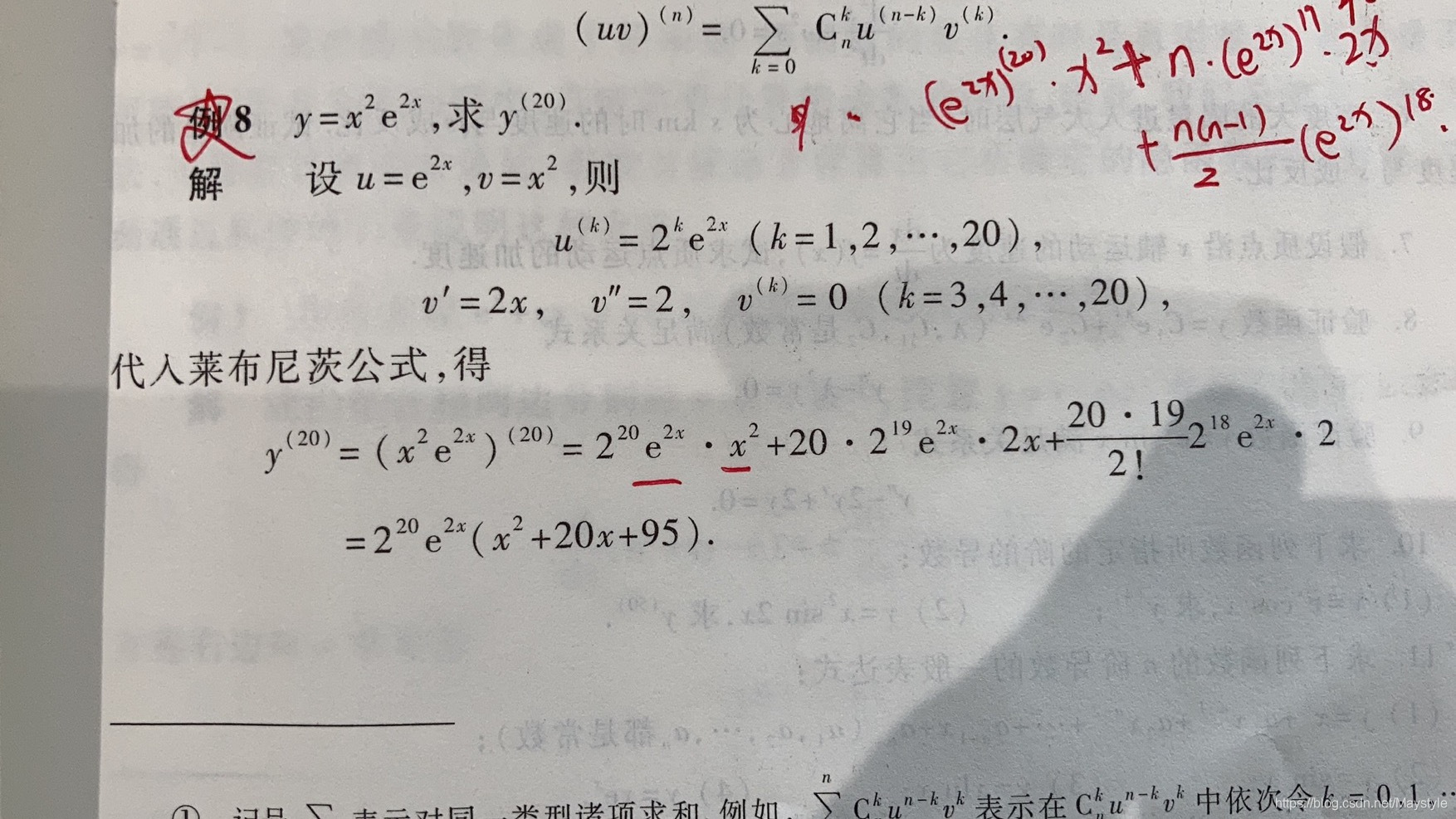
注意正负号:

阿巴阿巴计算:
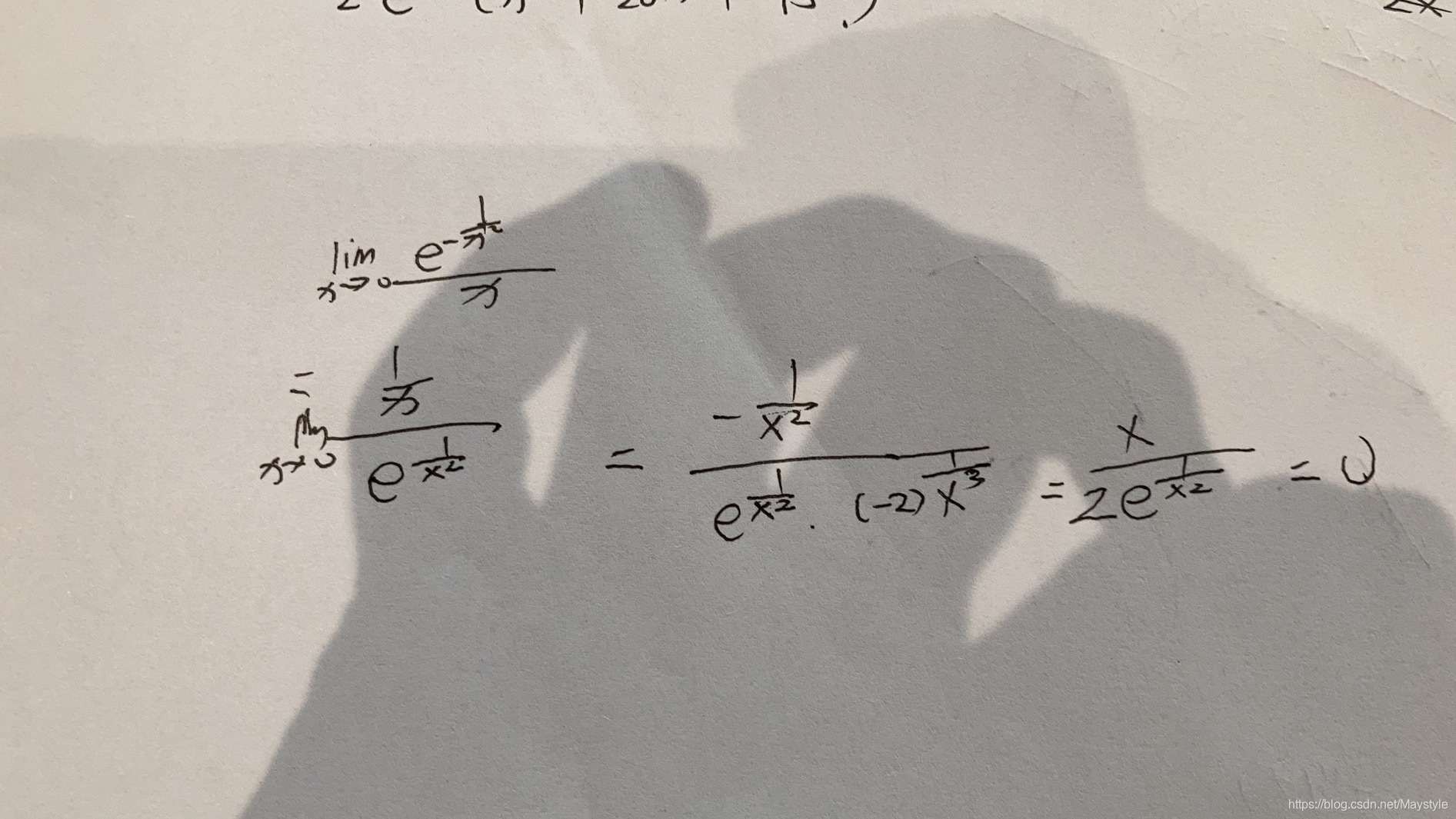
洛必达法则与凑导数:


某点的导数,以及趋于该点导函数的极限值的关系(通过洛必达法则)

绝对值函数的导数:


极限式表示的函数可导性:

导数、微分与增量的关系:

导数与幂级数(以及反函数求导):



阿巴阿巴:


拐点的条件:(类比极值)

渐近线求法:

曲率:

带有拉格朗日余项的泰勒公式:


证明数列收敛:


费马引理:

罗尔中值定理:

因子法和柯西中值定理:

运用两次罗尔定理:
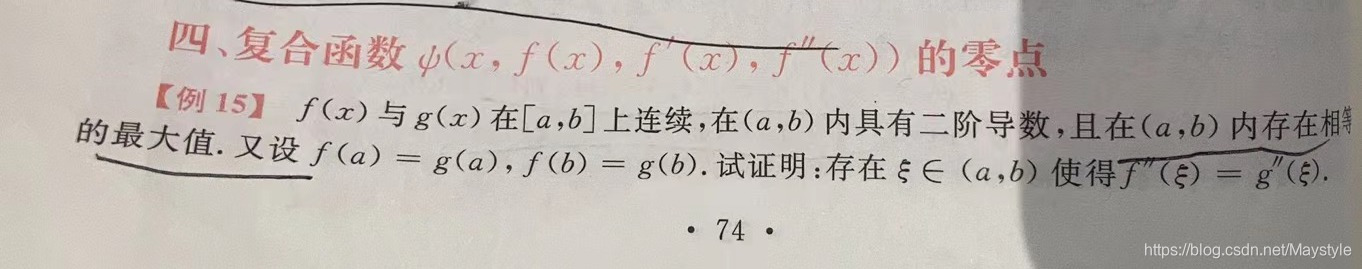
导函数与原函数的性质:

拉格朗日中值定理求极限

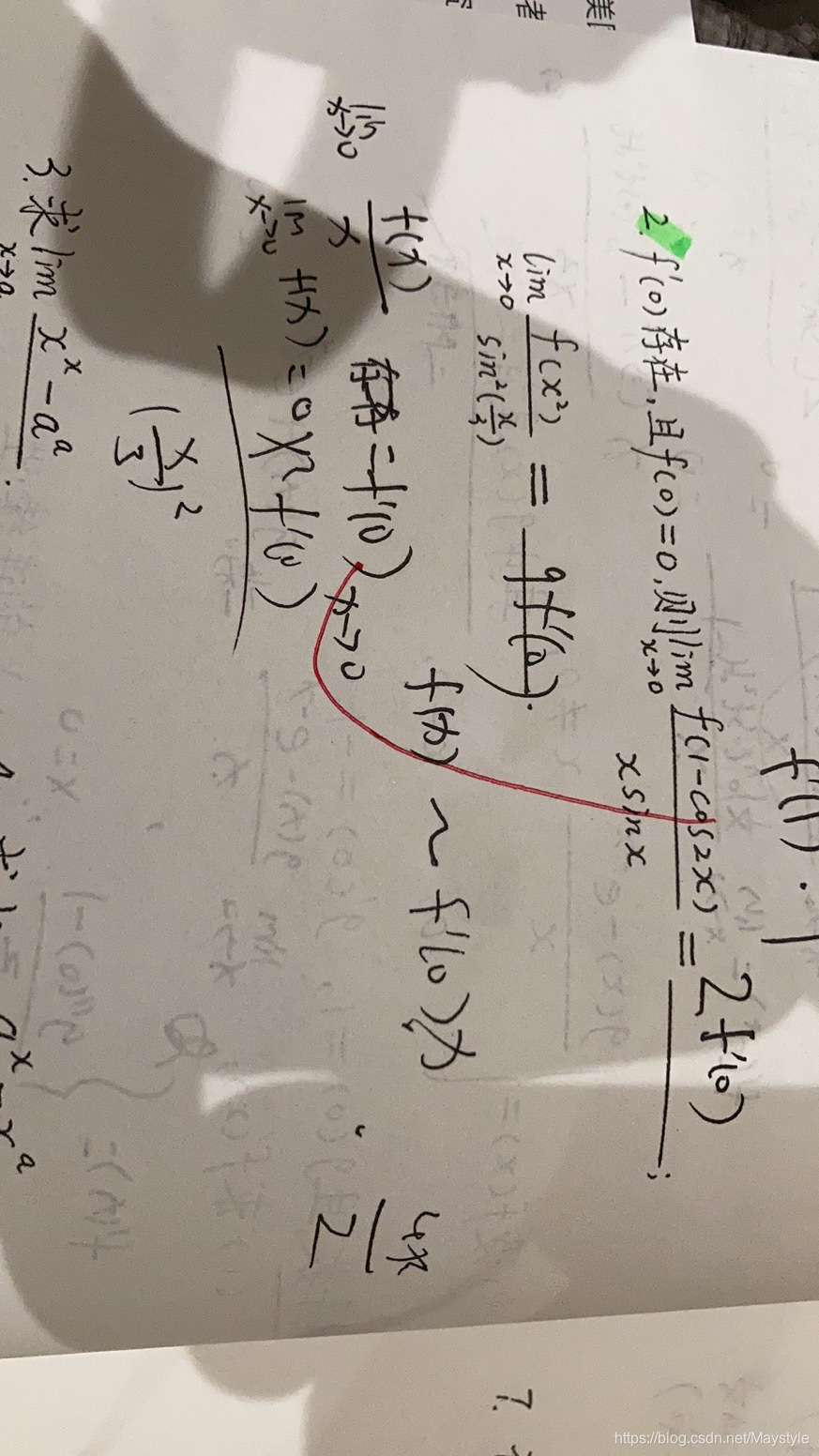
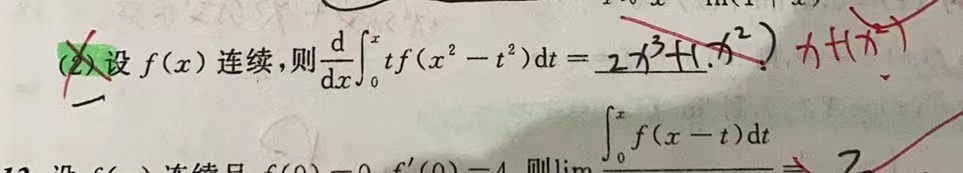








 博客围绕微积分展开,介绍了莱布尼茨公式、洛必达法则、绝对值函数导数等导数相关内容,还涉及极限式表示的函数可导性、导数与幂级数关系等。此外,阐述了拐点条件、渐近线求法、曲率等,以及罗尔、拉格朗日等中值定理的应用,如用拉格朗日中值定理求极限。
博客围绕微积分展开,介绍了莱布尼茨公式、洛必达法则、绝对值函数导数等导数相关内容,还涉及极限式表示的函数可导性、导数与幂级数关系等。此外,阐述了拐点条件、渐近线求法、曲率等,以及罗尔、拉格朗日等中值定理的应用,如用拉格朗日中值定理求极限。
















 4260
4260

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








