k-means算法原理及python代码

k-Means算法是一种聚类算法，它是一种无监督学习算法，目的是将相似的对象归到同一个蔟中。蔟内的对象越相似，聚类的效果就越好。聚类和分类最大的不同在于，分类的目标事先已知，而聚类则不一样。其产生的结果和分类相同，而只是类别没有预先定义。

算法原理

设计的目的：使各个样本与所在簇的质心的均值的误差平方和达到最小（这也是评价K-means算法最后聚类效果的评价标准）。

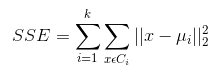
步骤

1. 创建k个点作为k个簇的起始质心（经常随机选择）。
2. 分别计算剩下的元素到k个簇中心的相异度（距离），将这些元素分别划归到相异度最低的簇。
3. 根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均值。
4. 将D中全部元素按照新的中心重新聚类。
5. 重复第4步，直到聚类结果不再变化。
6. 最后，输出聚类结果。

伪代码

创建k个点作为K个簇的起始质心（经常随机选择）
当任意一个点的蔟分配结果发生变化时（初始化为True）
	对数据集中的每个数据点，重新分配质心
		对每个质心
			计算质心到数据点之间的距离
		将数据点分配到距其最近的蔟
	对每个蔟，计算蔟中所有点的均值并将均值作为新的质心

• 优点：容易实现
• 缺点：可能收敛到局部最小值，在大规模数据上收敛较慢</