1 模型介绍

 针对无人机编队的通信拓扑切换问题,研究了一种基于联合误差的编队控制方法.基于无人机自身位置设置弹性前视点,通过各无人机间位置误差和速度误差,建立了带有联合误差的线性状态方程.引入编队中其他无人机之间的误差反馈,设计了一种弹性的扩展一致性控制器.经典的一致性控制是该扩展一致性控制律在某些无人机之间的误差未知情况下的一个特例.最后,应用Hurwitz稳定性分析方法验证了固定通信拓扑结构系统的稳定性,并给出了其稳定的充分条件.采用Lyapunov稳定性分析方法得出了切换通信拓扑结构的指数收敛的条件.仿真结果表明该方法在固定和切换的拓扑下均能保持稳定队形,而且弹性编队能很好地适应长机速度变化.

2 部分代码

clear; matlabrc; clc; close all;
  • 1.
addpath(genpath('controllers'))
  • 1.
addpath(genpath('dynamics'))
  • 1.
addpath(genpath('tools'))
  • 1.
% Initial Control gains:
  • 1.
k_ria = 20;  %(inter-agent position)
  • 1.
k_via = .26;  %(inter-agent velocities)
  • 1.
k_rvl = .5; %(virtual-leader position)
  • 1.
k_vvl = .25;  %(virtual-leader velocity)
  • 1.
k_obs = 10;   %(obstacle position)
  • 1.
exp = 4;
  • 1.
gains = [k_ria,k_via,k_rvl,k_vvl,k_obs]';
  • 1.
% Optimize:
  • 1.
options = optimoptions('fmincon','FiniteDifferenceStepSize',1e-1);
  • 1.
% A = [4 0 0 0 30/31.5];
  • 1.
% b = 0;
  • 1.
A =[];
  • 1.
b = [];
  • 1.
Aeq = [];
  • 1.
beq = [];
  • 1.
lb = [0 0 0 0 0];
  • 1.
ub = [];
  • 1.
x = fmincon(@simulate, gains, A,b,Aeq,beq,lb,ub,[], options);
  • 1.
%%
  • 1.
gains = x;
  • 1.
[ts, total_error, broke] = simulate_dev(gains,1);
  • 1.
total_error(total_error == 0) = [];
  • 1.
dt = 1e-1;
  • 1.
num_steps = length(total_error);
  • 1.
tfinal = num_steps*dt;
  • 1.
tspan = dt:dt:tfinal;
  • 1.
%%
  • 1.
figure()
  • 1.
plot(tspan,total_error); hold on
  • 1.
xlabel('Time (sec)')
  • 1.
ylabel('Total Error')
  • 1.
yl = ylim;
  • 1.
plot([broke broke],[yl(1) yl(2)],'--k')
  • 1.

3 仿真结果

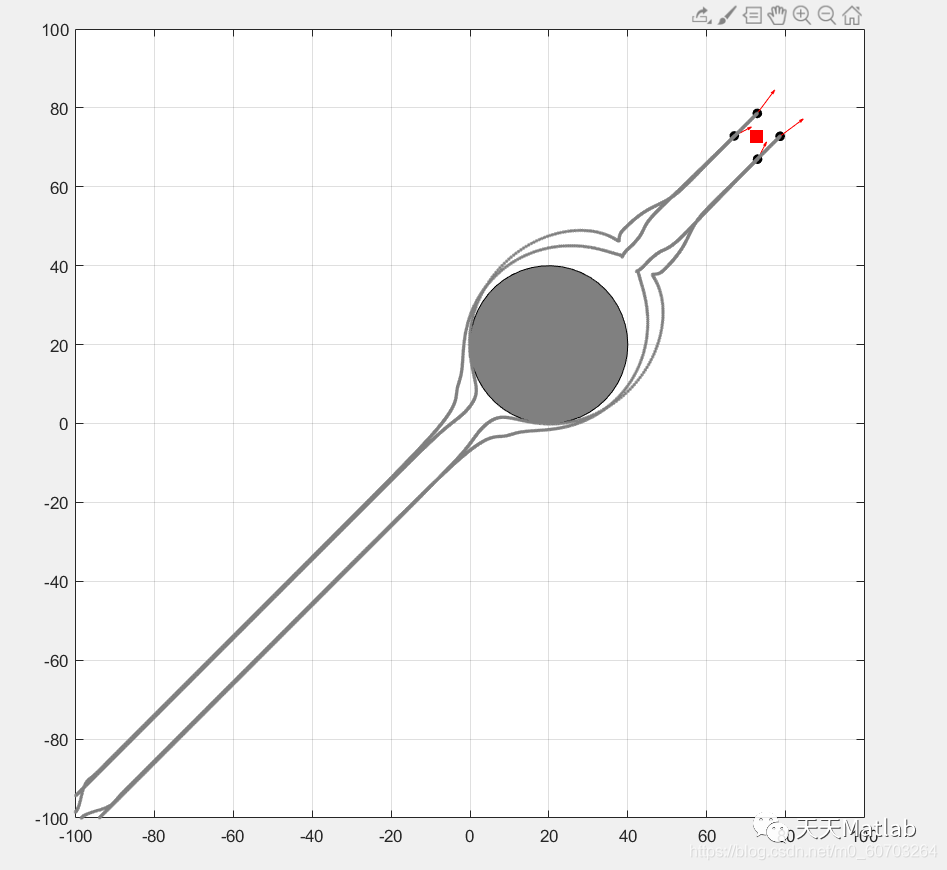
​【无人机导航】复杂环境下的无人机编队路径规划matlab源码_无人机

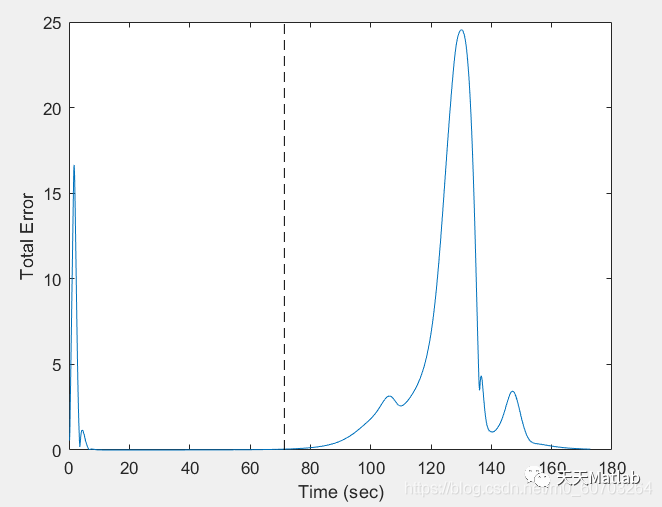
​【无人机导航】复杂环境下的无人机编队路径规划matlab源码_无人机_02

4 参考代码

[1]屈耀红, 闫建国. 曲线拟合滤波在无人机导航数据处理中的应用[J]. 系统工程与电子技术, 2004(12):1912-1914.

[2]熊涛, 曹科才, 柴运,等. 基于输入约束一致性算法的多无人机编队控制[J]. 计算机工程与应用, 2018, 054(012):51-56,125.

5 代码下载

​【无人机导航】复杂环境下的无人机编队路径规划matlab源码_无人机_03