💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
💥1 概述
基于DSP滤波器的加速度-速度-位移转换研究
1. DSP滤波器的基本原理及选型
加速度数据通常包含高频噪声和低频漂移,需通过数字滤波提取有效信号。DSP滤波器通过数字运算实现信号滤波,主要分为两类:
- FIR滤波器:
非递归结构,稳定性高,无相位失真,但计算量较大。适用于对相位敏感的场景(如实时运动控制)。其输出仅取决于当前和有限历史输入,数学表达式为: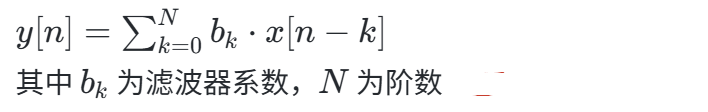
- IIR滤波器:
递归结构,计算效率高,但可能因反馈环路不稳定。适用于资源受限的实时系统,传递函数为: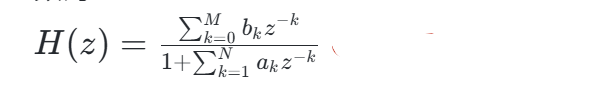
频域滤波类型选择:
| 滤波器类型 | 截止特性 | 适用场景 |
|---|---|---|
| 低通滤波器 (LPF) | 保留低频信号,抑制高频噪声 | 去除传感器高频噪声(如振动干扰)[3][42] |
| 高通滤波器 (HPF) | 保留高频信号,抑制低频漂移 | 消除重力加速度偏移 [42][50] |
| 带通滤波器 (BPF) | 保留特定频段信号 | 提取人体步态特征频段 [3][33] |
选型建议:巴特沃斯滤波器因通带平坦特性常用于加速度信号预处理,需根据信号频谱特征选择截止频率(如人体运动分析常用 0.1–10 Hz 带通)[42][33]。
2. 加速度数据滤波的关键方法
2.1 噪声特性与滤波策略
- 高频噪声:由传感器电子噪声或环境振动引起,采用LPF抑制(如截止频率 20 Hz)[42][35]。
- 低频漂移:积分导致的基线偏移,需HPF滤除(截止频率 0.1–0.5 Hz)[90][92]。
- 脉冲干扰:使用中值滤波(窗口大小 N=7N=7)或限幅滤波消除突发噪声 [46][39]。
动态滤波优化:
一阶惯性低通滤波器在静态时效果显著,但运动状态下易产生相位滞后。可通过动态阈值调整滤波参数:
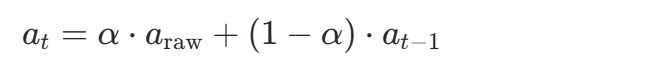
其中 α 根据运动状态自适应调整 [39]。
2.2 滤波算法实现示例(Python)
from scipy.signal import butter, filtfilt
# 巴特沃斯带通滤波设计
def bandpass_filter(data, lowcut, highcut, fs, order=4):
nyq = 0.5 * fs
low = lowcut / nyq
high = highcut / nyq
b, a = butter(order, [low, high], btype='band')
return filtfilt(b, a, data) # 双向滤波消除相位偏移
# 卡尔曼滤波(抑制积分漂移)
from pykalman import KalmanFilter
kf = KalmanFilter(transition_matrices=[1], observation_matrices=[1])
filtered_accel = kf.em(accel_raw).smooth(accel_raw)[0]
注:
filtfilt双向滤波避免相位失真,优于单向滤波 [35][95]。
3. 速度和位移的积分转换及误差控制
3.1 积分算法原理
3.2 积分误差来源与抑制技术
| 误差类型 | 产生原因 | 解决方案 |
|---|---|---|
| 趋势项漂移 | 低频噪声积分放大 | 高通滤波 + 动态零点校正 [92][95] |
| 累积误差 | 积分步长误差传递 | 频域积分法(FFT+精度控制方程)[98] |
| 相位偏移 | 滤波器群延迟 | 零相位滤波(如 filtfilt)[91] |
自适应鲁棒积分法 (ARI):
通过实时校正基线漂移,避免传统滤波导致的峰值误差和相位超前问题,位移计算误差降低 40% 以上 [91]。
4. DSP加速优化策略
4.1 硬件级加速
- FPGA实现FIR滤波器:
利用并行计算架构加速卷积运算,512阶FIR滤波器处理速度提升至软件实现的 50 倍 [159]。
- 专用DSP芯片:
TI C54X 系列支持单周期乘加运算,优化实时滤波性能 [8][62]。
4.2 算法级优化
- 多相抽取技术:
降低采样率减少计算量,结合存储器复用系数 [159]。 - HLS(高级综合)工具:
使用Catapult将C++代码自动转换为FPGA可综合RTL,缩短开发周期 [150]。
5. 应用案例与验证
5.1 人体运动分析
- 滤波方案:7点均值滤波(N=7N=7)去除加速度毛刺 。
- 位移精度:经卡尔曼滤波+离散积分,步长测量误差 < 2% 。
5.2 结构振动监测
-
对比实验:
方法 位移峰值误差 相位偏移 传统LPF积分 15–20% 显著超前 ARI法 < 5% 无偏移
6. 结论与展望
DSP滤波器通过噪声抑制和漂移控制,显著提升加速度积分精度。未来方向包括:
- 深度学习融合:训练自适应滤波器参数选择模型;
- 边缘计算优化:基于低功耗DSP芯片的实时处理架构;
- 多传感器融合:结合陀螺仪数据补偿旋转运动误差。
核心建议:设计滤波器时需权衡计算效率与相位特性(首选零相位FIR),积分阶段必须采用动态漂移校正(如ARI或卡尔曼滤波)以抑制累积误差。
📚2 运行结果



部分代码:
%% Processed inputs
%--------------------------------------------------------------------------
time = data(:,1); % Time vector
accval_g = data(:,2); % Acceleration in g
accval = data(:,2)*9.81; % Acceleration in m/s^2
L = size(data,1); % Length of signal
Fs = 1/(time(2)-time(1)); % Sampling frequency
Ts = 1/Fs; % Sampling period
%% Displacement, Velocity and Acceleration
%--------------------------------------------------------------------------
[~, ~, ~, filtered_acc_g] ...
= accelo2disp(time,Ts, Fs, Fcut,alpha, accval_g, Lvdtmat,...
lvdtcons, accbiasV, accsensi, filtertype...
,filtermethod,firorder);
[LVDTfilt, filtered_disp, filtered_vel, filtered_acc] ...
= accelo2disp(time,Ts, Fs, Fcut,alpha, accval, Lvdtmat,...
lvdtcons, accbiasV, accsensi, filtertype...
,filtermethod,firorder);
%% Compute the frequency
%--------------------------------------------------------------------------
% Compute the Fourier transform of the signal.
Y = fft(filtered_acc);
% Compute the two-sided spectrum P2. Then compute the single-sided spectrum P1
% based on P2 and the even-valued signal length L.
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
% Define the frequency domain f and plot the single-sided amplitude spectrum P1.
% On average, longer signals produce better frequency approximations.
f = Fs*(0:(L/2))/L;
%% Plot Acceleration vs.time
%--------------------------------------------------------------------------
figure;
subplot(5,2,1)
ax1 = plot(time, accval_g, 'LineWidth', 1);
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($g$)','Interpreter', 'latex');
title('Acceleration vs.time (with DC bias)')
ax2 = subplot(5,2,2);
plot(time, filtered_acc_g, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($g$)','Interpreter', 'latex');
title('Acceleration vs.time (DC bias removed)')
ax3 = subplot(5,2,3:4);
plot(time,filtered_acc, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($\frac{m}{s^2}$)','Interpreter', 'latex');
title('Acceleration vs.time (DC bias removed)')
ax4 = subplot(5,2,5:6);
plot(time,filtered_vel, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Velocity ($\frac{m}{s}$)','Interpreter', 'latex');
title('Velocity vs.time')
ax5 = subplot(5,2,7:8);
plot(time,filtered_disp, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Displacement ($m$)','Interpreter', 'latex');
title('Displacement vs.time')
ax6 = subplot(5,2,9:10);
plot(f,P1, 'LineWidth', 1)
grid on
title('Frequency Spectrum of Acceleration')
xlabel('f(Hz)')
ylabel('|P1(f)|')
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]张熹彦.基于可调谐滤波器和DSP的波长解调算法研究及软件设计[D].东南大学,2009.DOI:10.7666/d.y1651500.
[2]刘翔,李哲英.FIR滤波器的速度优化方法研究[C]//全国第十届信号与信息处理、第四届DSP应用技术联合学术会议.0[2024-02-26].




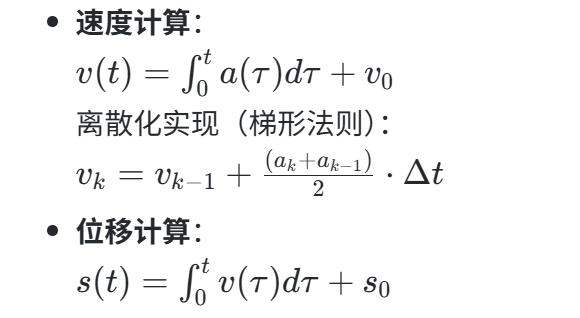
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








