💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
💥1 概述
摘要:我们利用copula构建了一个统一的框架,用于在层次贝叶斯模型中构建和优化变分提议。针对具有连续且非高斯隐藏变量的模型,我们提出了一种半参数化和自动化的变分高斯copula方法,其中参数化的高斯copula族能够保留多变量后验依赖性,而基于Bernstein多项式的非参数转换则在描述单变量边缘后验时提供了充分的灵活性。
关键词:统计学 - 机器学习 计算机科学 - 学习 统计学 - 计算
本文提出了一个统一的变分Copula推断框架。在VGC中,我们着重于高斯Copula族以简化问题,然而,其他更灵活的形式,如高斯混合Copula,也可以考虑进来。为了避免为隐藏变量指定边缘的困难,基于Bernstein多项式的非参数程序间接地引入了高度灵活的单变量边缘。Tran等人和Kucukelbir等人可能会从我们的灵活边缘中受益,而我们的方法可能会从藤Copula分解中受益,以允许更丰富或更复杂的依赖关系,并应用于Kucukelbir等人中的自动微分技术。
详细文章见第4部分。
变分高斯Copula推断中基于Bernstein多项式的非参数转换在描述单变量边缘后验时的灵活性研究
一、研究背景与核心问题
变分推断(Variational Inference, VI)通过优化变分分布逼近真实后验,在处理大规模数据时效率显著,但传统方法(如均值场近似)假设隐变量独立,忽略后验依赖关系,导致近似偏差。高斯Copula变分推断(VGC)通过分离边缘分布与依赖结构,保留变量间相关性,但单变量边缘后验的建模仍依赖参数化假设(如高斯或混合高斯分布),难以捕捉复杂形状(如多峰、偏态、重尾等),限制了推断准确性。
二、Bernstein多项式非参数转换的原理与优势
-
万能逼近能力
Bernstein多项式是连续函数的加权和,其阶数(控制点数量)增加时,可无限逼近任意连续边缘累积分布函数(CDF)。这一性质使其无需预设边缘分布形式,直接从数据中学习复杂形状,克服参数化方法的局限性。 -
单调性与概率约束
通过约束多项式权重为非负且和为1,可确保转换函数单调非降,满足概率分布的基本要求(如CDF单调性)。这一特性简化了边缘分布建模,避免非参数方法中常见的约束处理难题。 -
与变分框架的兼容性
Bernstein多项式转换函数可导,其导数(边缘概率密度函数,PDF)可通过自动微分框架高效计算。这使得变分优化目标(如证据下界ELBO)的梯度可解析求解,支持基于梯度下降的优化算法,与变分推断流程无缝集成。 -
灵活性控制
多项式阶数(K)作为超参数,平衡模型灵活性与计算效率:- 低阶:适用于简单边缘形状(如单峰对称分布),参数少、计算快。
- 高阶:捕捉复杂形状(如多峰、偏态),但参数增加可能导致过拟合。
实际应用中可通过交叉验证或信息准则(如AIC、BIC)选择最优K。
三、方法实现与关键步骤
-
基准分布选择
通常选择标准正态分布作为基准分布,因其数学性质良好且易于采样。转换后的边缘分布为:
F(x)=BK(Φ(σx−μ)),BK(u)=k=0∑Kωk(kK)uk(1−u)K−k
其中,Φ为标准正态CDF,BK为Bernstein多项式,ωk为权重参数。
-
权重优化
通过最小化变分分布与真实后验的KL散度(或最大化ELBO),优化权重ωk及其他变分参数(如Copula相关参数)。优化算法可采用随机梯度下降(SGD)或其变体(如Adam),结合自动微分工具(如PyTorch、TensorFlow)高效计算梯度。 -
边缘PDF计算
边缘PDF为基准分布PDF与Bernstein多项式导数的乘积:
p(x)=ϕ(σx−μ)⋅dudBK(u)u=Φ(σx−μ)
其中,ϕ为标准正态PDF,多项式导数可通过权重差分解析求解。
四、实际应用中的优势
-
提高推断准确性
通过灵活捕捉边缘后验的真实形状,变分近似更接近真实后验,减少偏差。例如,在金融风险模型中,可更准确估计资产收益的偏态分布,提升风险价值(VaR)预测精度。 -
增强模型鲁棒性
参数化方法在真实后验与假设不符时可能失效,而非参数转换对形状假设更少,适应性强。例如,在生物医学数据中,可处理基因表达量的多峰分布,避免参数模型的系统性偏差。 -
保留边缘信息
非参数转换全面保留边缘分布特征(如峰值位置、尾部厚度),支持更精细的依赖结构建模。在多变量时间序列分析中,可准确刻画变量间非线性依赖,提升预测性能。 -
广泛适用性
该方法可与各类基于高斯Copula的变分推断模型结合,适用于复杂数据集(如高维、非正态、离散-连续混合)和贝叶斯模型(如层次模型、非线性状态空间模型)。
五、挑战与未来方向
-
超参数选择
Bernstein多项式阶数K需手动调优,未来可探索自适应选择方法(如基于贝叶斯优化或信息准则的自动调参)。 -
计算效率优化
高阶多项式增加参数数量,可能导致优化困难。可研究结构化表示(如低秩近似)或高效优化算法(如自然梯度下降)以提升计算速度。 -
高维扩展
当前研究聚焦单变量边缘,未来需结合高维Copula结构(如藤Copula)或稀疏依赖建模,处理高维数据中的复杂依赖关系。 -
与其他非参数方法对比
可比较Bernstein多项式与归一化流(Normalizing Flows)、核密度估计等方法的优劣,探索混合建模策略(如用Bernstein多项式建模边缘,用神经网络建模依赖)。
六、结论
基于Bernstein多项式的非参数转换通过其万能逼近能力、单调性约束和变分框架兼容性,为变分高斯Copula推断中的单变量边缘后验建模提供了充分灵活性。该方法显著提升了推断准确性、鲁棒性和信息保留能力,适用于复杂数据和贝叶斯模型。尽管面临超参数选择和计算效率等挑战,其潜力为精确多元后验推断开辟了新路径,值得进一步研究与应用。
📚2 运行结果
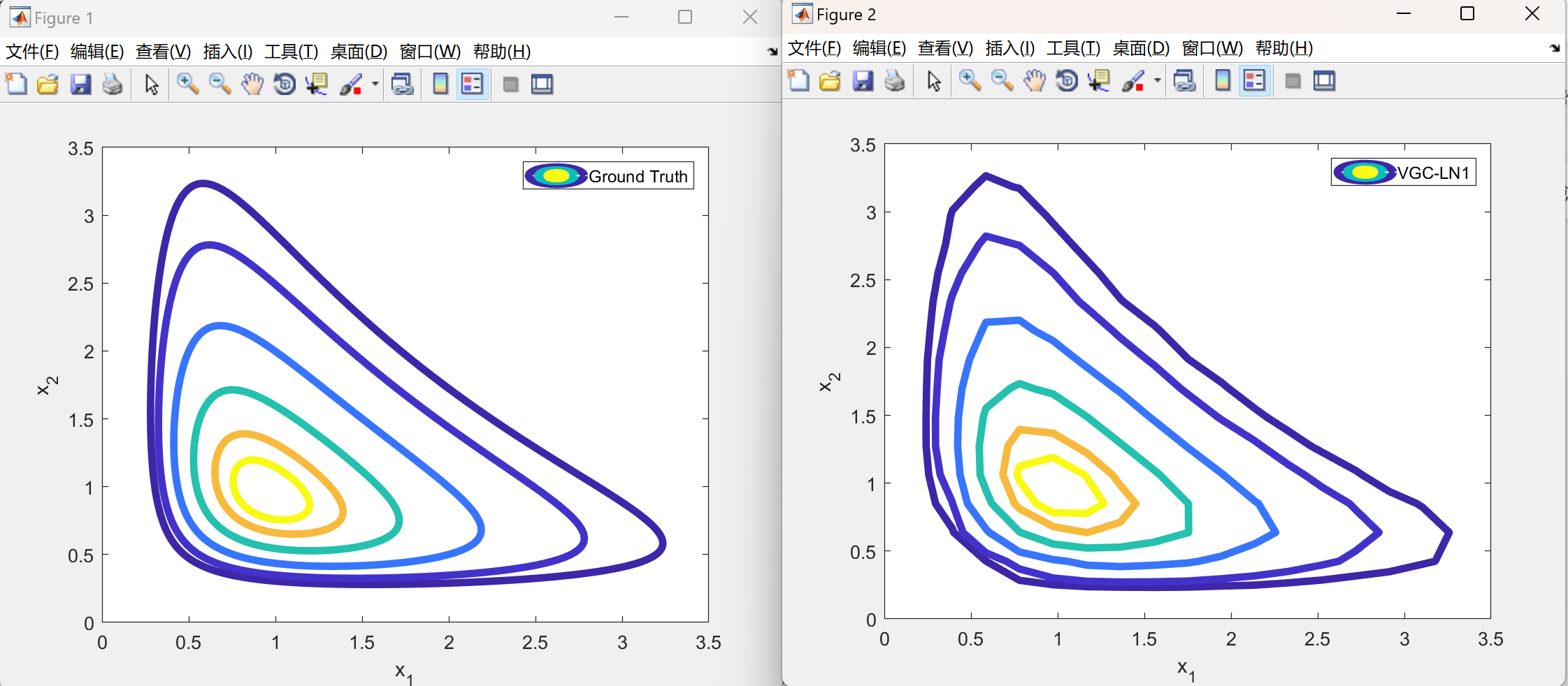
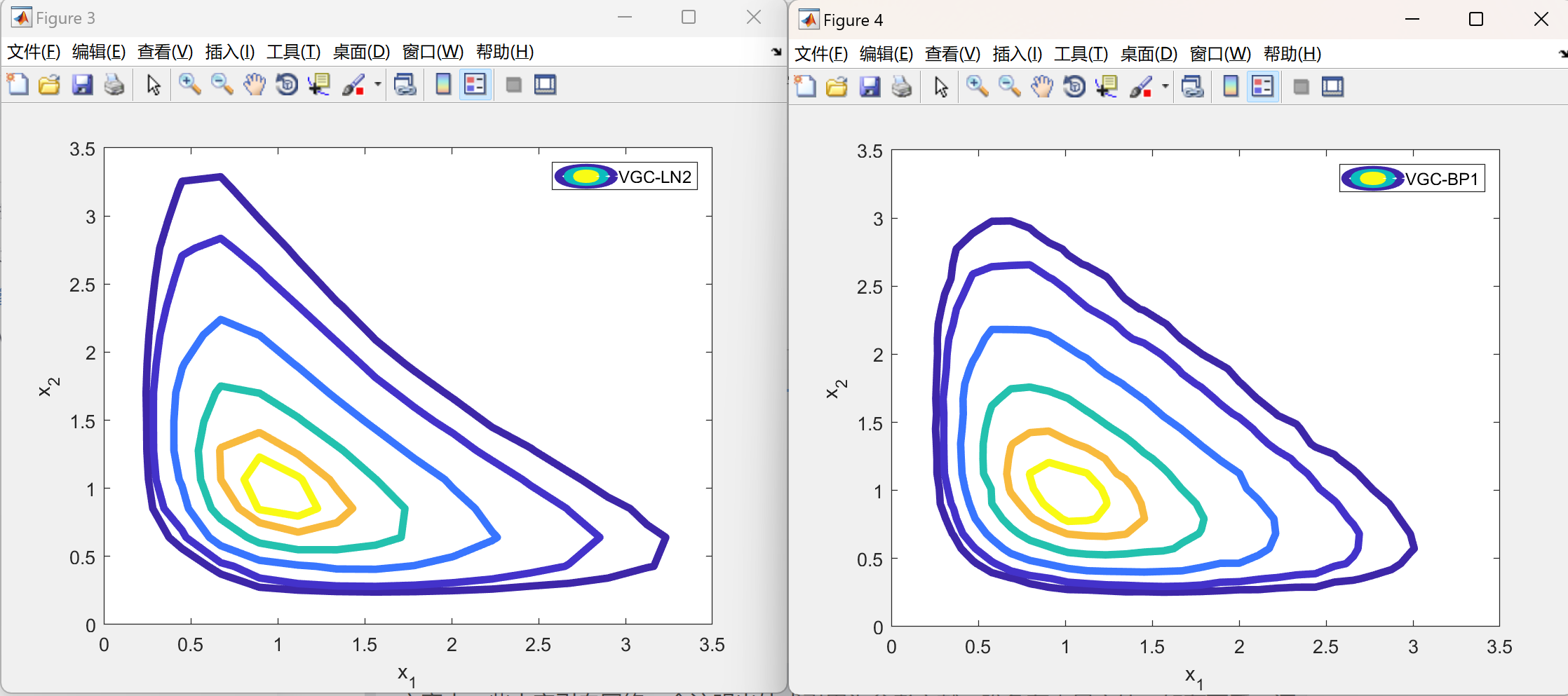
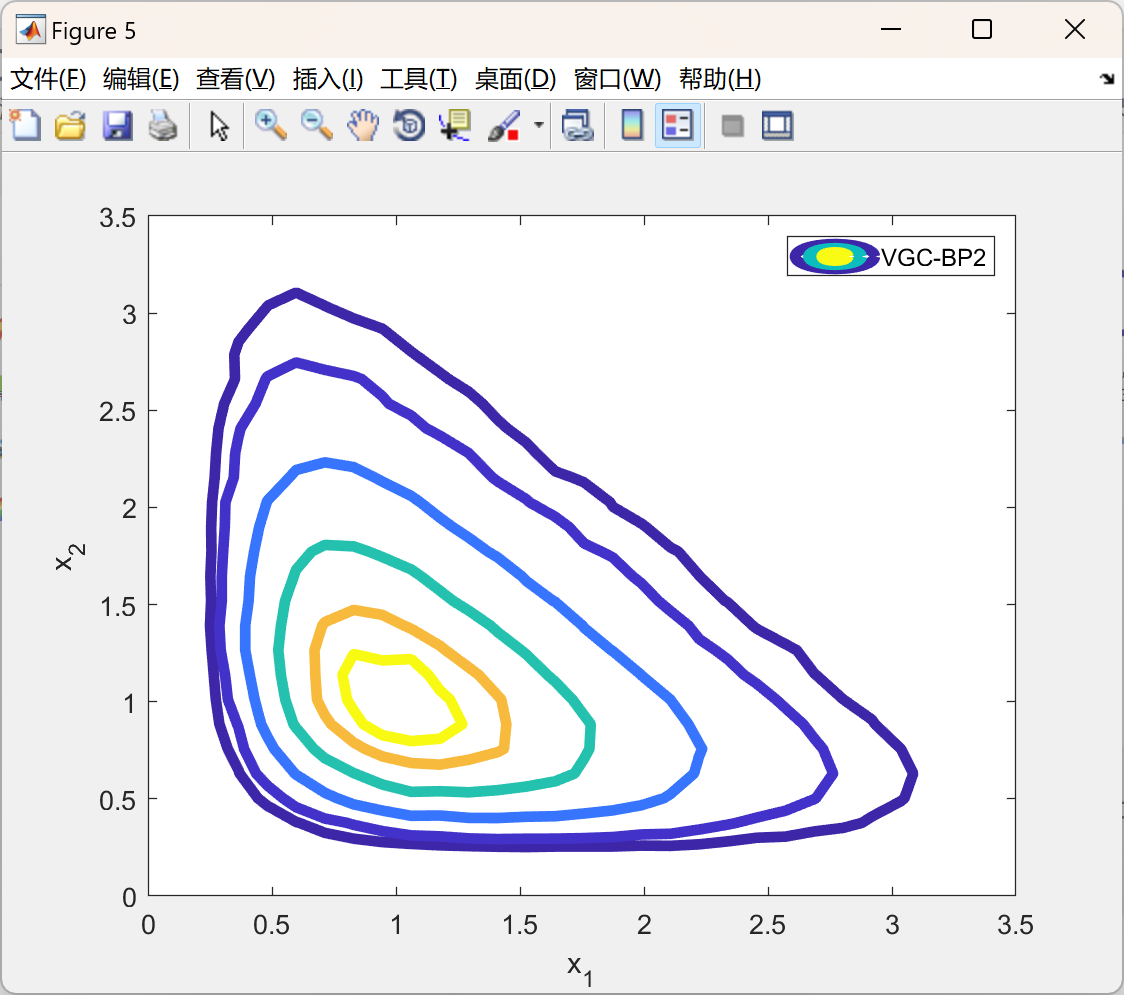
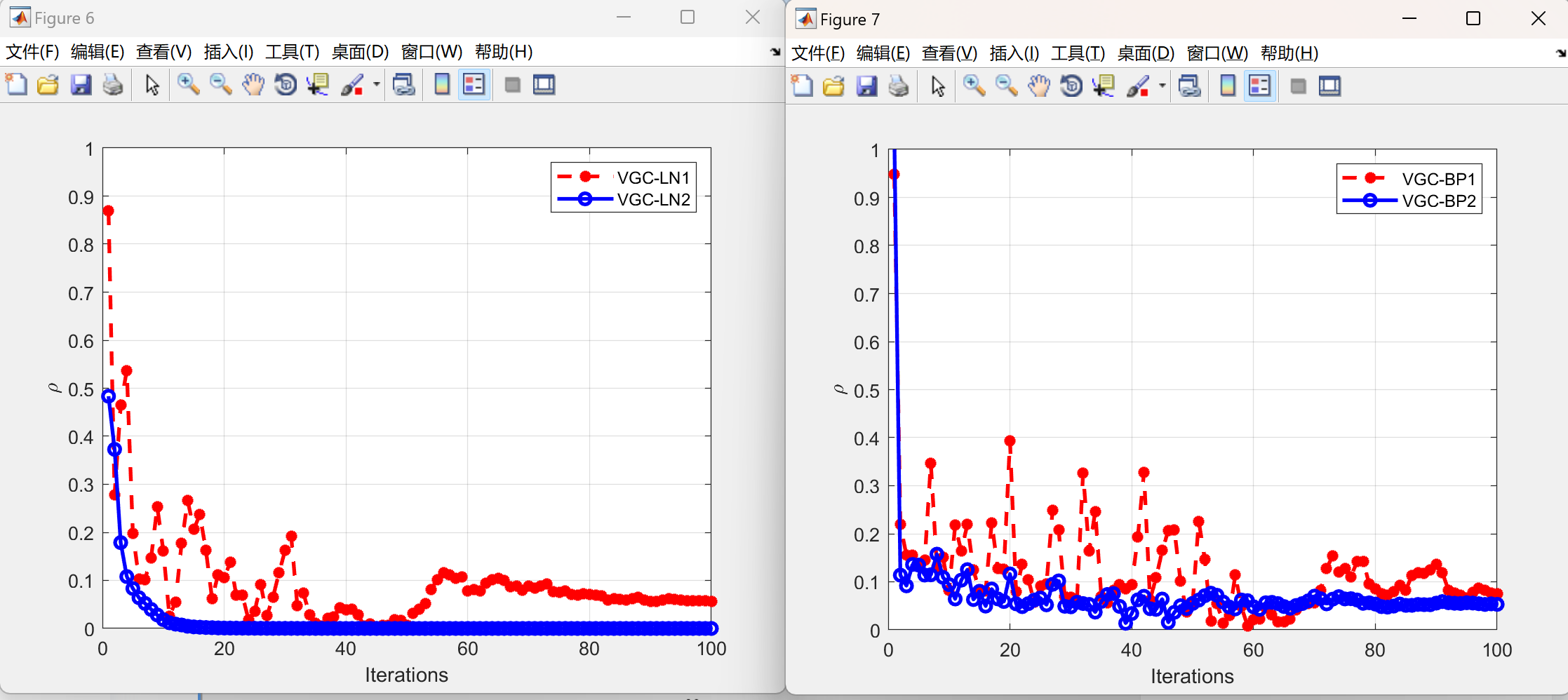
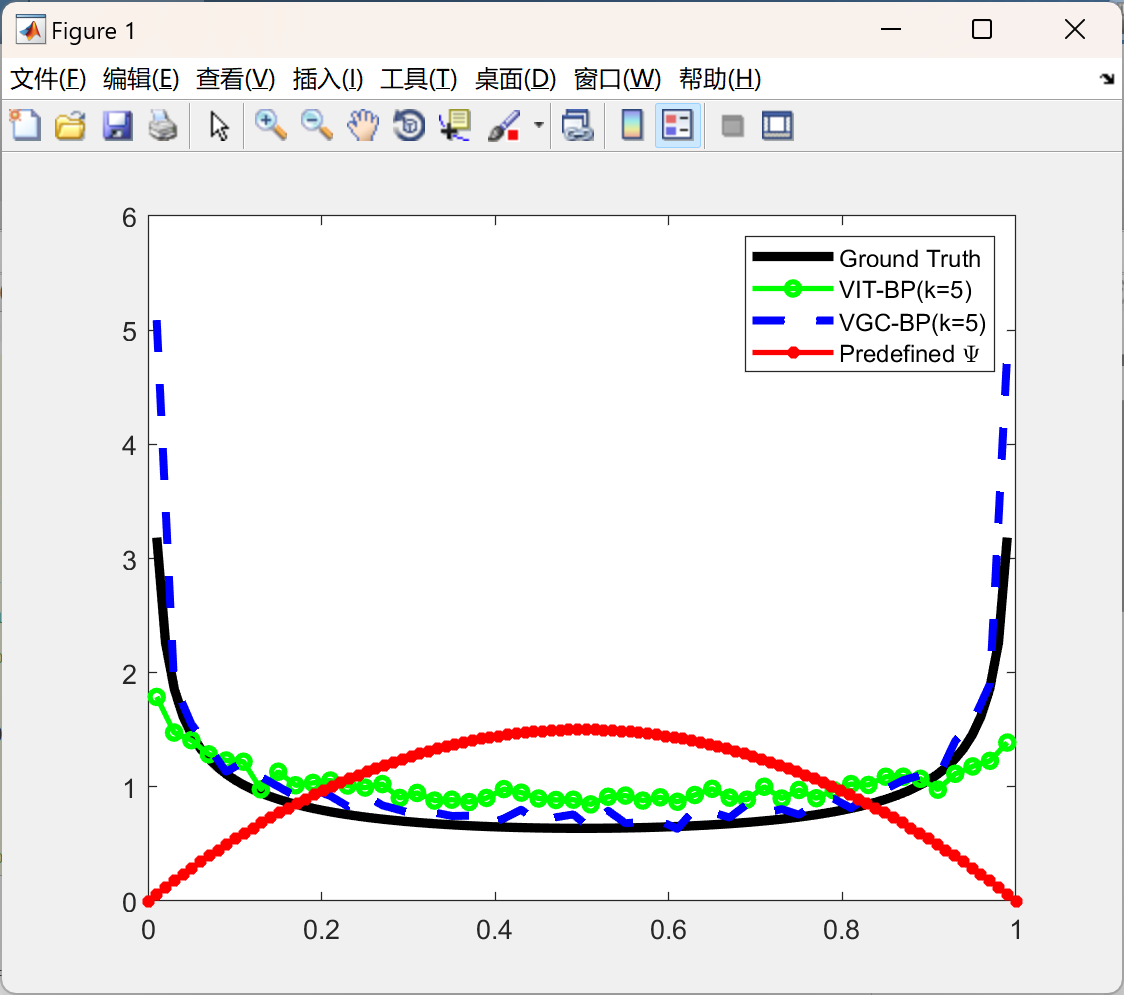
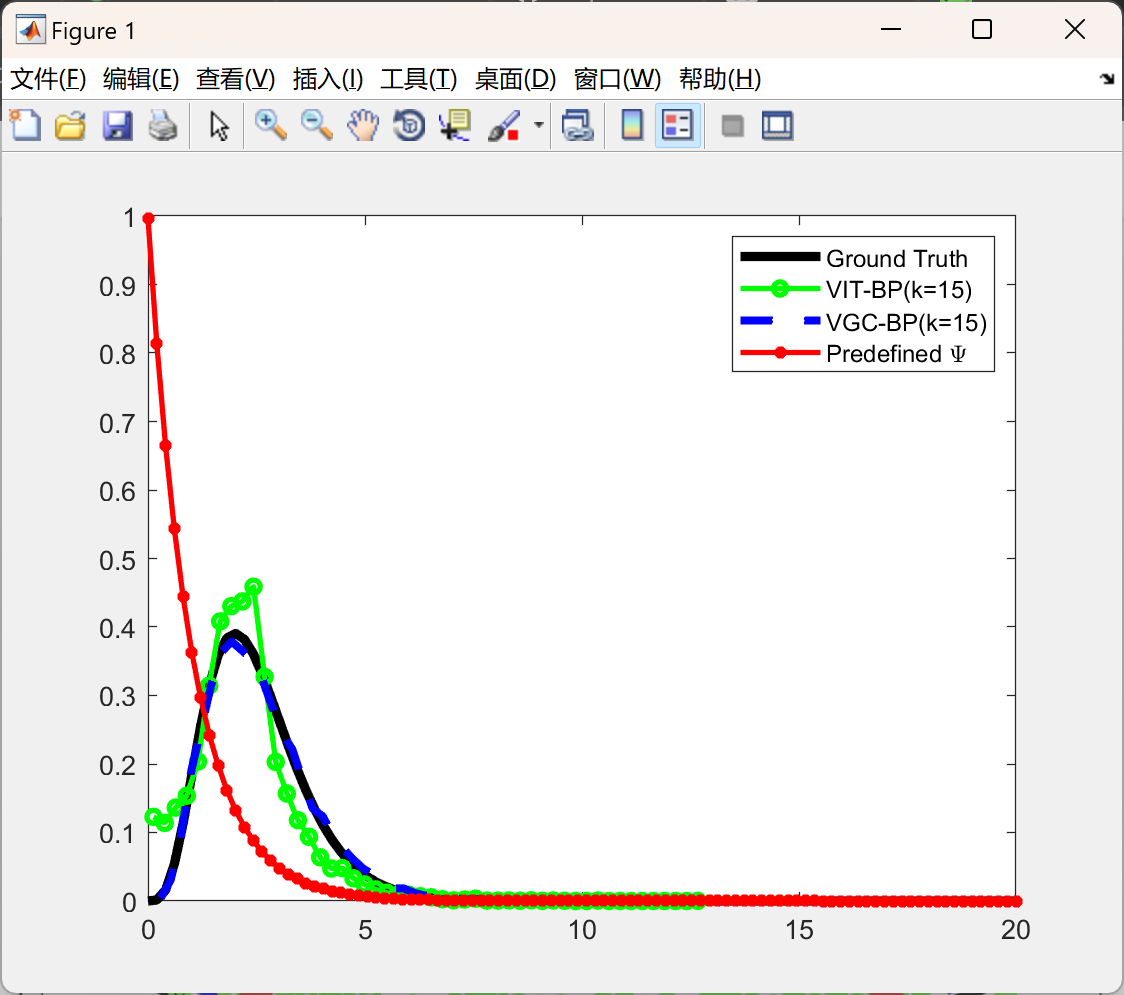
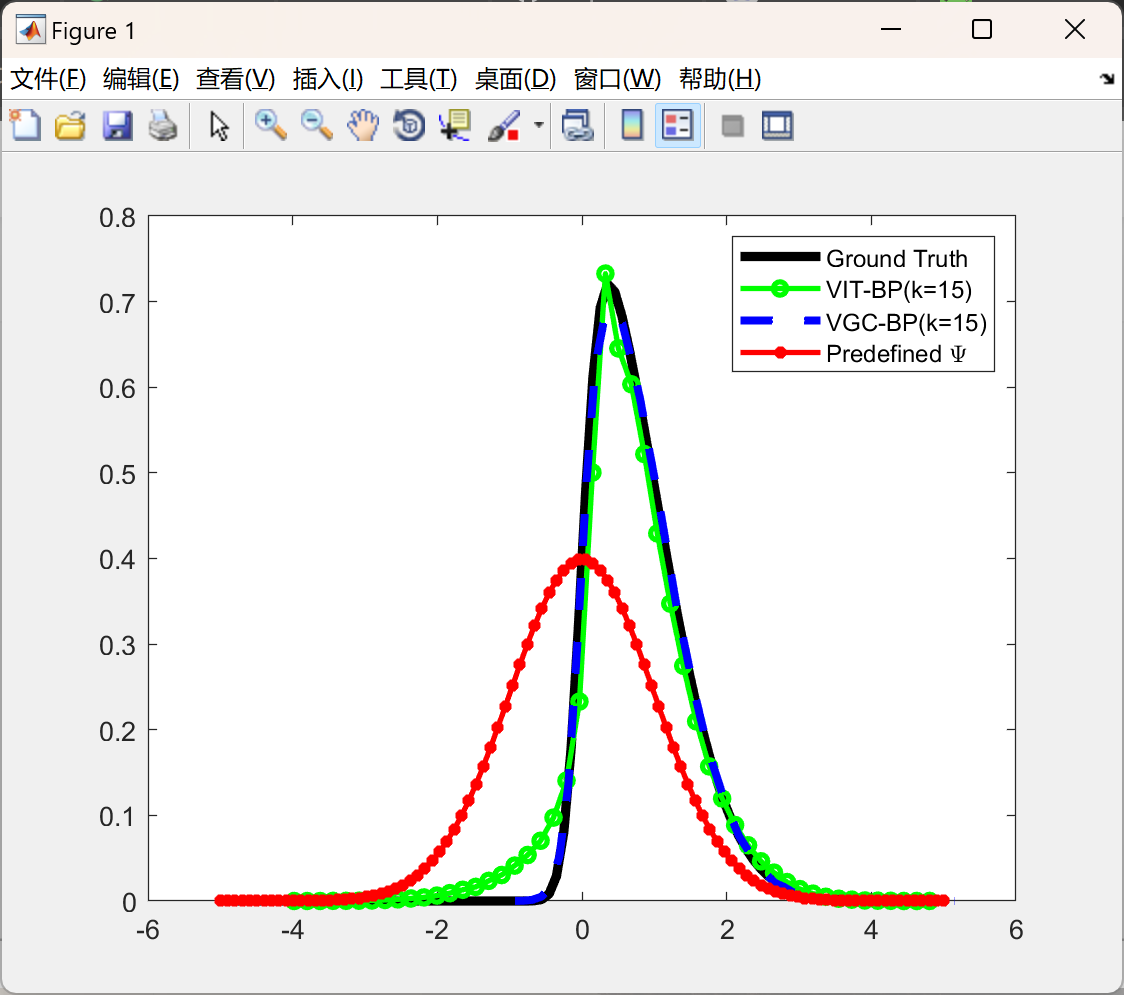
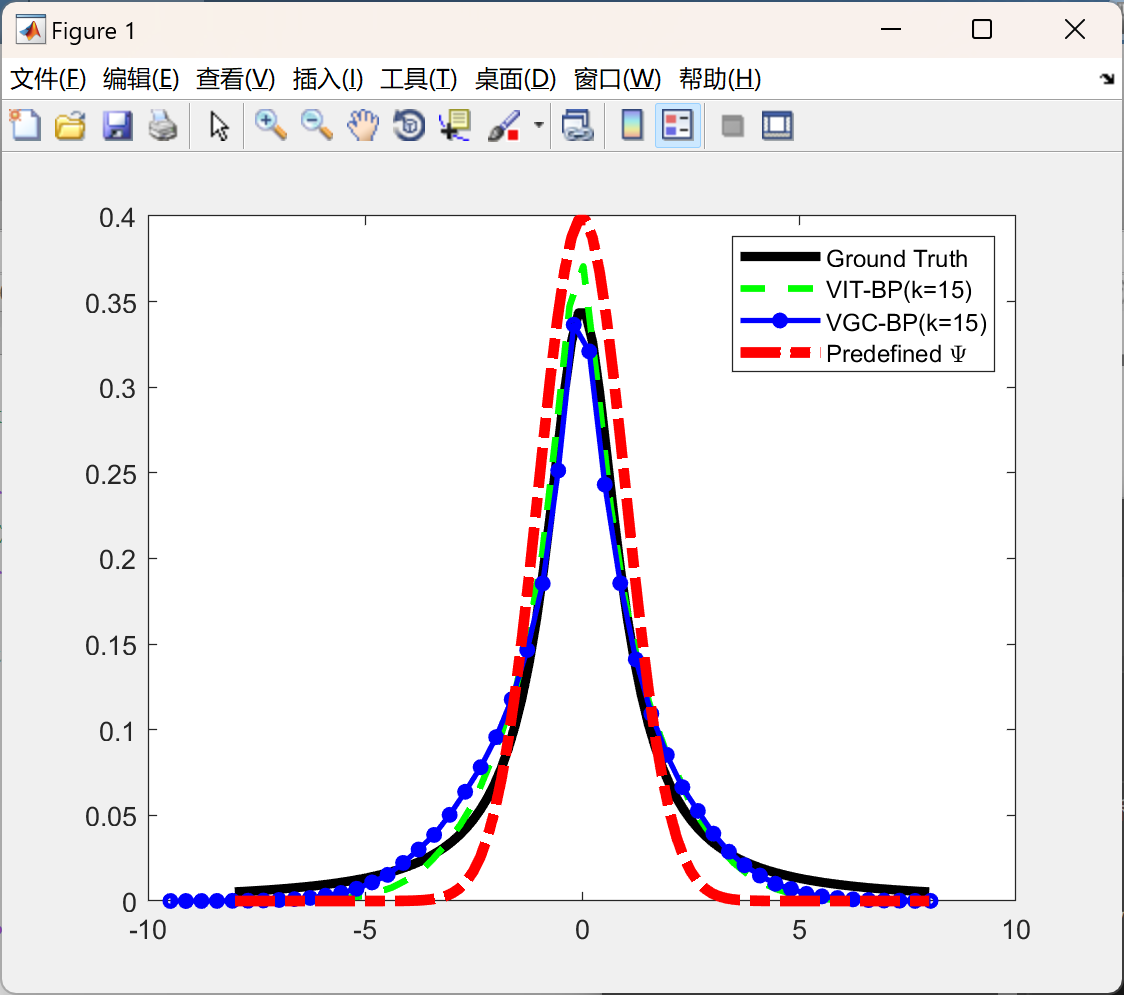
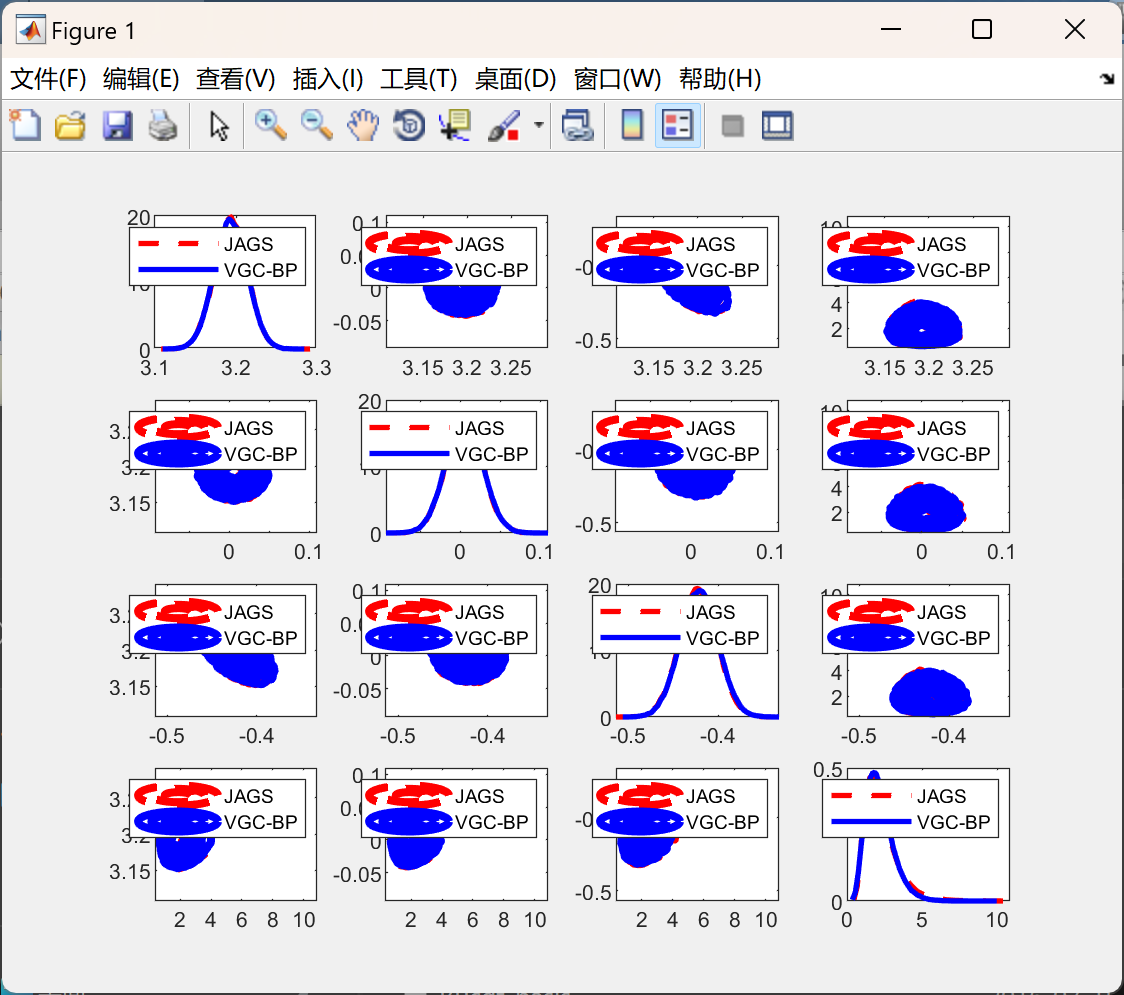
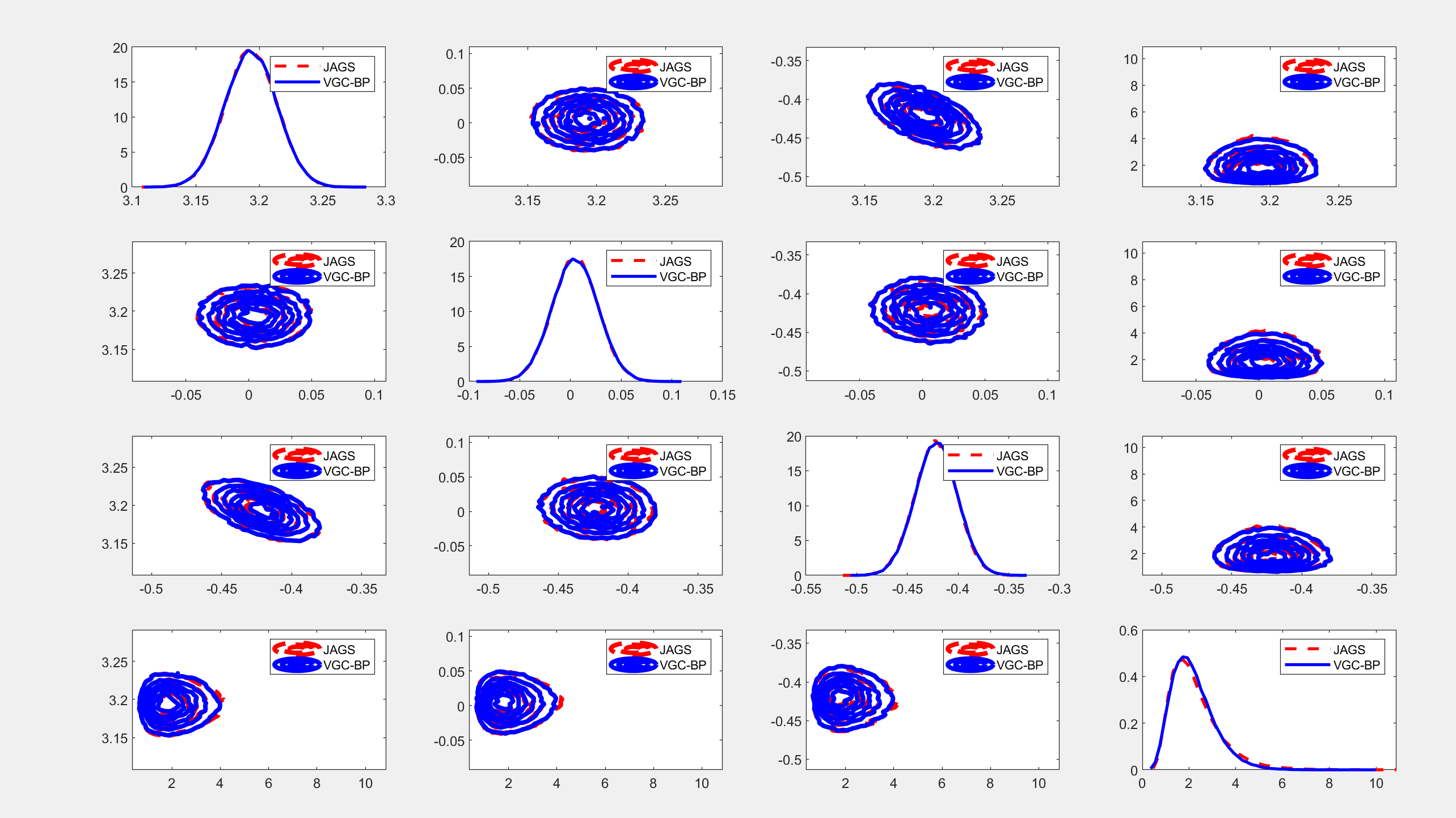
部分代码:
%%
opt.k = 15; % Degree/Maximum Degree of Bernstein Polynomials
opt.MaxIter = 50; % Number of SGD stages
opt.NumberZ = 1; % Average Gradients
opt.InnerIter = 500; % Number of iteration
opt.N_mc = 1; % Number of median average in sELBO stepsize search
BPtype = 'BP'; % Bernstein Polynomials
% BPtype = 'exBP'; % Extended Bernstein Polynomials
% PsiType = 'Normal'; opt.PsiPar(1) = 0; opt.PsiPar(2) = 1; % variance
PsiType = 'Exp'; opt.PsiPar = 1;
PhiType = 'Normal'; opt.PhiPar(1) = 0; opt.PhiPar(2) =1; % variance
% Learning rate
opt.LearnRate.Mu = 0.001; opt.LearnRate.C =1e-3;
opt.LearnRate.W = 1e-3; opt.LearnRate.dec = 0.95; % decreasing base learning rate
switch BPtype
case 'BP'
opt.D = opt.k;
case 'exBP'
opt.D = opt.k*(opt.k+1)/2; % # of basis functions
end
% Diagonal constraint on Upsilon
opt.diagUpsilon = 0;
%% Initialization
ini.Mu = opt.PhiPar(1).*ones(fix.P,1);
ini.C = opt.PhiPar(2).*eye(fix.P);
ini.w = randBPw(fix.P, opt.D, 1, 1);
% ini.w = 1./opt.D.*ones(fix.P, opt.D);
% Median Outlier Removal
opt.OutlierTol = 10; % Threshold for online outlier detection
opt.WinSize = 20; % Size of the window
opt.Wthreshold = 1e8; opt.normalize = 0;
ini.WinSet = ini_WinSet(trueModel, PhiType, PsiType, BPtype, fix, opt, ini);
%% VGC-(Uniform)Adaptive Algorithm
[ELBO, par] = vgcbp_w(trueModel, inferModel, PhiType, PsiType, BPtype,fix, ini, opt);
opt.nsample = 2e4;
Y_svc = sampleGC(PhiType, PsiType, BPtype, opt, par);
Y_svc(sum(~isfinite(Y_svc),2)~=0,:) = [];
figplot.nbins = 50;
[figplot.f_x1,figplot.x_x1] = hist(Y_svc, figplot.nbins);
% VCSBPC = hist1D2D(Y_svc, nbins);
%% VGC-(Non-Uniform) Algorithm
opt.adaptivePhi = 0; VGmethod = 'Numeric';
[ELBO2, par2] = vgcbp_MuCW(trueModel, inferModel, PhiType, PsiType, BPtype, VGmethod, fix, ini, opt);
Y_svc2 = sampleGC(PhiType, PsiType, BPtype, opt, par2);
Y_svc2(sum(~isfinite(Y_svc2),2)~=0,:) = [];
[figplot.f_x2,figplot.x_x2] = hist(Y_svc2, figplot.nbins);
%% Plot
figplot.nb = 100; figplot.Seqx = linspace(0, 20, figplot.nb)';
figplot.log_pM = logmodel(figplot.Seqx, trueModel, fix);
trueModel2 = PsiType; fix2.lambda = opt.PsiPar; fix2.c = 1;
figplot.log_pM2 = logmodel(figplot.Seqx, trueModel2, fix2);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。




















 796
796

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








