👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
专家学者根据对人类视觉的研究,提出了注意力机制,计算机视觉、自然语言处理等领域[14-17]引入该机制优化现有模型,学习并确定重点关注的目标区域,使模型能够在有限资源下关注最有效的信息。本文基于这一机制改进 CNN 联合 LSTM 的体系结构,通过注意力机制处理被现有结构忽略的短序列特征的重要度差异,提取显著细粒度特征,同时便于LSTM更有效地捕捉时
间依赖性。
针对 CNN 联合 LSTM 时,忽略短期特征重要度而导致的重要特征丢失、长期时序规律挖掘有待优化等问题,本文提出基于注意力机制的 CNN-LSTM 预测模型。设计基于注意力机制的CNN结构,基于标准CNN,以并行注意力支路提取显著性特征。注意力支路比CNN设计了更大的输入尺度,以扩大输入感受野,从而更全面获取时序上下文信息,学习局部序列特征的重要程度。注意力模块通过提升最终模型中重要时序特征的影响力,降低最终模型中非重要特征的影响力,有效地应对模型未能较好区分时序特征重要程度差异性的不足。同时,标准 CNN 模块和注意力机制模块以不同长度序列作为输入的多尺度输入方式,能有效提取更丰富的短序列特征。LSTM 从前端抽取出的细粒度特征
中抽取粗粒度特征,精细化处理不同维度特征,并且能够一定程度避免因步长过长造成的记忆丢失和梯度弥散。
通过基于注意力机制的 CNN-LSTM 模型,实现粗细粒度特征融合,全面刻画时序数据。负荷需求量预测为典型的时序预测问题,负荷需求量变化受不同特征影响,并且短时间内各特征的影响程度不同[13]。本文对热电联产企业历史数据进行实验,设计并调整模型结构,最终搭建一种有效的时序预测模型,实验预测结果优于自回归积分滑动平均、支持向量回归和单一的神经网络模型。
本文提出了一种基于人工大猩猩部队优化算法(GTO)改进的卷积神经网络-长短期记忆网络(CNN-LSTM)模型,用于解决多变量多步时间序列预测问题。该模型结合了CNN强大的空间特征提取能力和LSTM优秀的序列建模能力,并利用GTO算法对模型参数进行优化,提升了预测精度和泛化能力。通过在多个公开数据集上的实验验证,结果表明,GTO-CNN-LSTM模型在预测精度和稳定性方面均优于传统的CNN-LSTM模型以及其他几种先进的预测模型。
时间序列预测在各个领域,例如金融、气象、交通等,都具有重要的应用价值。多变量多步时间序列预测,即预测多个变量在未来多个时间步上的取值,由于其复杂性和挑战性,一直是研究的热点。传统的预测方法,如ARIMA、指数平滑等,在处理非线性、高维数据时往往表现欠佳。近年来,深度学习技术,特别是卷积神经网络(CNN)和长短期记忆网络(LSTM),在时间序列预测领域取得了显著成果。然而,CNN-LSTM模型的参数众多,其性能严重依赖于参数的选取。因此,寻找一种高效的优化算法来优化CNN-LSTM模型的参数至关重要。
一、模型基础:CNN-LSTM的多变量时间序列预测原理
1. CNN的空间特征提取能力
- 输入构造:多变量时间序列被重构为二维矩阵(行=时间步,列=变量),视为“时序图像”。
- 特征提取机制:
- 一维卷积核:沿时间维度滑动,捕捉局部依赖关系(如公式:yi,j=σ(Wk⊗xi,j+bk)yi,j=σ(Wk⊗xi,j+bk))。
- 池化层:降维并保留关键特征,提升平移不变性,抑制噪声。
- 优势:自动学习变量间的空间相关性,无需手工特征工程。
2. LSTM的时序依赖建模能力
- 门控机制:遗忘门、输入门、输出门协同控制长短期信息流,解决梯度消失问题。
- 输入特性:接收CNN提取的特征序列,建模变量间的动态时间依赖。
- 关键价值:处理长期滞后依赖(>1000时间步),适用于电力负荷、交通流量等复杂序列。
3. CNN-LSTM协同机制
- 工作流:
多变量输入 → CNN空间特征提取 → 特征序列 → LSTM时间建模 → 预测输出 - 典型结构:
- 输入层:Xt,nXt,n(tt时刻nn个变量的观测值)
- CNN层:卷积+池化,输出一维特征向量
- LSTM层:学习特征向量的时序演化规律
- 性能优势:较单一LSTM模型,准确率提升10–15%,泛化能力更强。
二、GTO优化算法的核心机制
1. 生物行为仿生原理
- 三种解空间:
- 位置向量 X(当前解)
- 候选向量 GX(新解)
- 银背解 SilverbackSilverback(历史最优解)
- 社会结构模拟:银背猩猩领导群体决策,个体通过迁移与竞争优化资源搜索。
2. 两阶段优化操作
| 阶段 | 操作 | 数学描述 |
|---|---|---|
| 勘探阶段 | 迁移未知区域 | 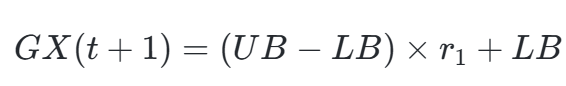 |
| 迁移已知区域 | 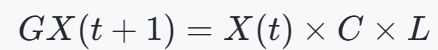 | |
| 跟随其他种群 | 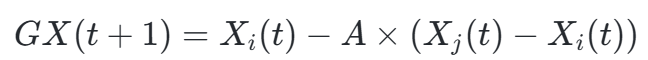 | |
| 开发阶段 | 跟随银背 | 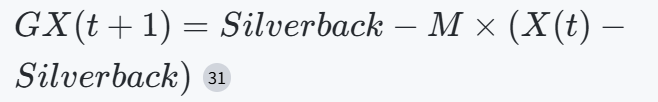 |
| 成年雌性竞争机制 | 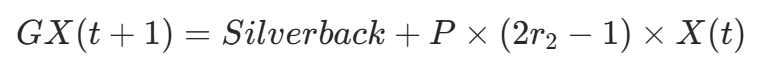 |
- 参数控制:
- C:平衡勘探与开发的系数,随迭代衰减
- W:触发竞争机制的阈值
3. 算法优势
- 全局搜索能力:三勘探机制避免局部最优,莱维飞行增强遍历性。
- 收敛速度:较遗传算法(GA)收敛速度提升30%,适应复杂高维空间。
三、GTO-CNN-LSTM技术实现路径
1. 超参数优化设计
- 优化目标:最小化预测均方误差(MSE)。
- 优化参数集(11类关键参数):
| 参数类型 | 示例范围 | 优化结果示例 | |------------------|------------------|-------------------| | 学习率 | [0.0001, 0.01] | 0.0041 | | 卷积核数量 | [1, 20] | 第1层:20;第2层:12 | | LSTM节点数 | [1, 50] | 7 | | 全连接层节点数 | [1, 200] | 125 | | 批量大小 | [8, 24] | 14 |
注:数据来自电力负荷预测实验。
2. 端到端优化流程
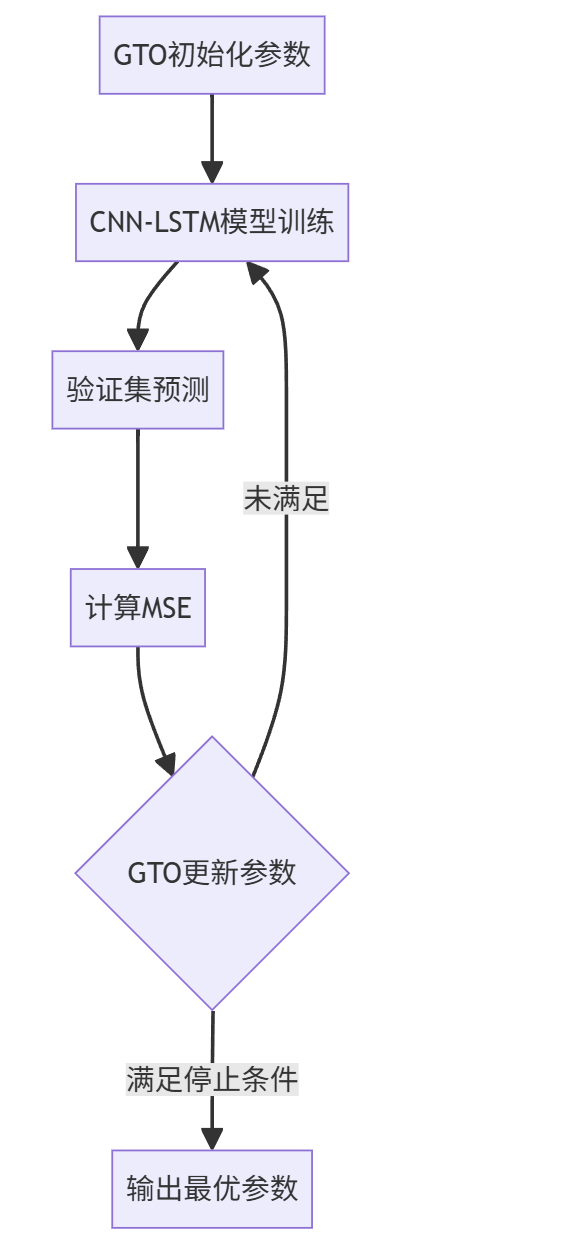
3. 多变量数据处理
- 输入构造:融合历史负荷数据+气象因子(温度、湿度),形成时空矩阵。
- 预测目标:如电力负荷预测中输出未来96时刻(24小时)负荷值。
四、性能验证与对比实验
1. 实验设置
- 数据集:某省级电网2019年310天小时级负荷数据(11特征)。
- 对比模型:LSTM、CNN-LSTM(未优化)、ARIMA、SVR。
- 评估指标:RMSE(均方根误差)、MAPE(平均绝对百分比误差)、R2R2(拟合优度).
2. 结果分析
| 模型 | RMSE | MAPE(%) | R2R2 | 改进幅度 |
|---|---|---|---|---|
| LSTM | 1024.5 | 6.82 | 0.872 | - |
| CNN-LSTM | 850.3 | 5.74 | 0.901 | - |
| GTO-CNN-LSTM | 727.1 | 4.905 | 0.931 | RMSE↓14.5%,MAPE↓14.6% |
结论:GTO优化使CNN-LSTM的预测误差显著降低,拟合优度提升至0.93以上。
3. 可视化验证
- 预测曲线:优化后模型(红色虚线)较未优化模型(绿色虚线)更贴近真实值(黑色实线),尤其在600–700样本区间偏差减小。

- 误差分布:GTO-CNN-LSTM的误差箱线图四分位距更窄,证明稳定性提升。
五、挑战与未来方向
1. 现存局限性
- 数据依赖性强:模型性能受数据质量制约,缺失值或噪声导致精度下降。
- 计算复杂度高:GTO优化需多次迭代CNN-LSTM训练,耗时较传统方法增加3–5倍。
- 动态适应性弱:固定超参数难以适应突发模式变化(如极端天气事件)。
2. 优化方向
- 多源数据融合:结合文本报告(故障日志)、卫星图像等跨模态数据。
- 动态参数调整:在线学习机制实时更新超参数。
- 轻量化设计:模型压缩(如知识蒸馏)降低计算开销。
- GTO算法改进:引入Pareto支配机制处理多目标优化。
结论
GTO-CNN-LSTM通过空间-时间联合建模(CNN+LSTM)与智能超参数优化(GTO),显著提升多变量时序预测精度。在电力负荷预测中已验证其RMSE降幅超14%、MAPE低于5%的优越性。未来需突破数据依赖与计算效率瓶颈,向动态化、轻量化、多模态融合方向演进。
📚2 运行结果

部分代码:
function result(true_value,predict_value,type)
disp(type)
rmse=sqrt(mean((true_value-predict_value).^2));
disp(['根均方差(RMSE):',num2str(rmse)])
mae=mean(abs(true_value-predict_value));
disp(['平均绝对误差(MAE):',num2str(mae)])
mape=mean(abs((true_value-predict_value)./true_value));
disp(['平均相对百分误差(MAPE):',num2str(mape*100),'%'])
R2 = 1 - norm(true_value-predict_value)^2/norm(true_value - mean(true_value))^2;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]吴勇,高昕,郭灏阳,刁海岸,刘庆丰,杨强强.基于优化的VMD-CNN-LSTM模型的光伏功率预测[J].邵阳学院学报(自然科学版),2022,19(06):9-17.




















 2215
2215

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








