💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
三、UFC 3-340-02与TM 5-855-02的异同点
💥1 概述
本文涵盖了以下内容:
- 爆炸载荷参数:包括爆炸药剂的特性、产生的爆炸压力、冲击波、破片及热辐射等信息。
- 建筑物和结构物的响应:介绍了建筑物和结构物受到爆炸作用时的响应及破坏机制,如振动、应力、位移等。
- 安全设计准则:提供了设计工程和基础设施时需要遵循的安全准则,以减轻爆炸压力效应对结构物、人员和设备的影响。
- 防爆保护措施:包括爆炸抗冲击设计、隔离区域规划、材料选用和防爆装置的使用等,以提高建筑物和设备的抗爆性能。
爆炸载荷参数
爆炸载荷参数是评估爆炸影响的基础,涵盖了多个关键方面:
- 爆炸药剂的特性:不同种类的炸药具有不同的爆炸能量和反应速度,这些特性直接影响爆炸产生的压力和冲击波强度。
- 爆炸压力:爆炸瞬间释放的能量转化为高压气浪,形成冲击波,对周围环境产生压力效应。
- 冲击波:冲击波是爆炸压力效应的主要表现形式,其传播速度、峰值压力和持续时间等参数是评估爆炸危害的重要指标。
- 破片:爆炸产生的破片对周围物体和人员构成直接威胁,其大小、形状和速度等特性决定了其破坏力。
- 热辐射:爆炸产生的热量以辐射形式向外传播,对周围环境和人员造成热伤害。
建筑物和结构物的响应
当爆炸发生时,建筑物和结构物会受到严重的冲击和破坏,其响应机制包括:
- 振动:爆炸冲击波引起的振动会对建筑物结构造成损伤,甚至导致倒塌。
- 应力:爆炸产生的压力波在建筑物结构中传播,形成应力集中区域,可能导致结构破坏。
- 位移:爆炸冲击波的作用会使建筑物产生整体或局部的位移,影响结构的稳定性和安全性。
安全设计准则
为了减轻爆炸压力效应对结构物、人员和设备的影响,需要遵循以下安全设计准则:
- 合理选址:避免将重要设施建在潜在爆炸危险区域附近。
- 结构加固:通过增加结构强度、提高材料韧性等措施,增强建筑物的抗爆性能。
- 防爆设施:设置防爆墙、防爆门等防爆设施,以阻挡或削弱爆炸冲击波的传播。
- 人员疏散:制定完善的人员疏散计划,确保在爆炸发生时能够迅速撤离危险区域。
防爆保护措施
除了遵循安全设计准则外,还可以采取以下防爆保护措施:
- 爆炸抗冲击设计:通过优化结构设计、选用抗爆材料等措施,提高建筑物的抗冲击能力。
- 隔离区域规划:在潜在爆炸危险区域周围设置隔离带,以减少爆炸冲击波对周围环境和人员的影响。
- 材料选用:选用具有良好抗爆性能的材料,如高强度钢材、防爆玻璃等。
- 防爆装置的使用:安装防爆装置,如防爆阀、泄爆口等,以释放爆炸产生的能量,减轻对建筑物的破坏。
基于UFC 3-340-02 / TM 5-855-02的爆炸压力效应研究对于提高建筑物的抗爆性能、保障人员和设备的安全具有重要意义。未来,随着科技的不断进步和爆炸防护技术的不断发展,我们将能够更有效地应对爆炸威胁,保护人民生命财产安全。
一、UFC 3-340-02中爆破载荷参数的核心内容
1. 关键参数定义与计算
UFC 3-340-02详细规定了爆炸载荷的物理参数及其计算方法,主要包括:
- 峰值超压(Peak Overpressure) :爆炸冲击波在自由场或反射条件下的最大压力值。对于球形TNT装药,通过比例距离Z=R/W1/3Z=R/W1/3(RR为爆距,WW为TNT当量)查图表或经验公式确定(图8对比了模拟与规范结果)。
- 冲量(Impulse) :冲击波压力随时间积分的总和,分为入射冲量irir和反射冲量isis,通过ZZ值查表获取。
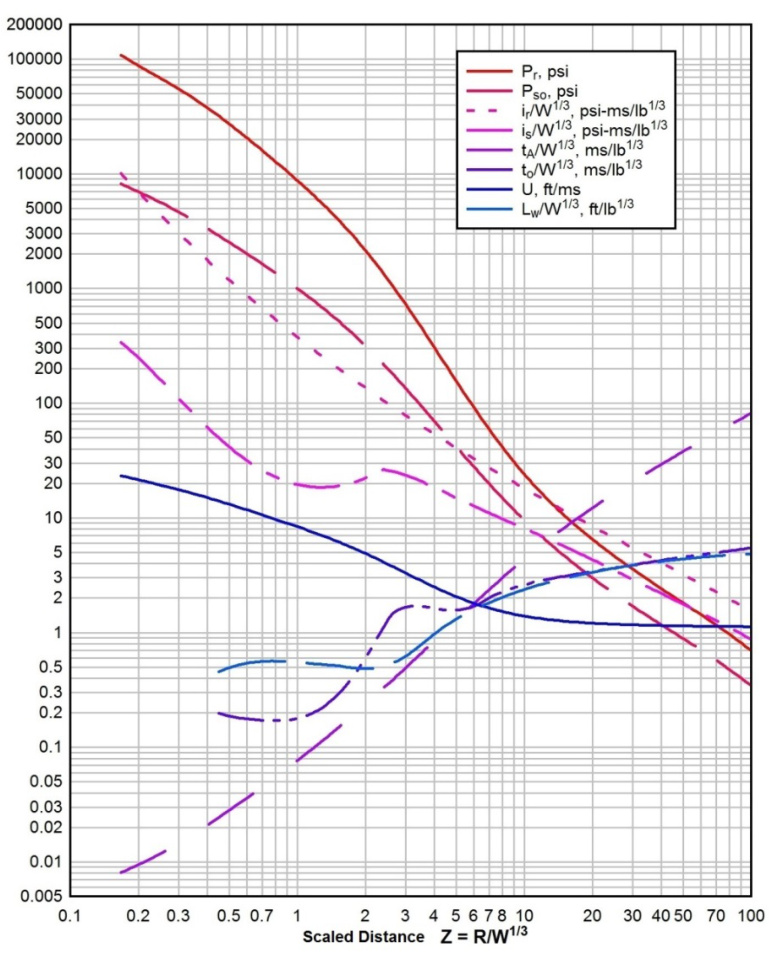
- 正压持续时间(Positive Phase Duration) :超压从峰值衰减至环境压力的时间,与比例距离相关。
- 层裂参数(Spallation Parameter) :引入参数ψ=R0.926fc0.266Wadj0.353ψ=R0.926fc0.266Wadj0.353,结合混凝土抗压强度fcfc和等效炸药量WadjWadj,划分层裂破坏区域。
- 舱内爆炸双三角形载荷:包括短时冲击波和长时准静态气压,用于模拟密闭空间内的爆炸效应(图3)。
2. 应用场景与设计准则
- 结构响应分析:通过动态载荷下的等效静力法(SDOF模型)评估构件的最大位移和失效模式。
- 泄漏压力计算:考虑爆炸波通过开口进入建筑内部的压力衰减,参考Section 2-15.5和1-11的流程。
- 材料适用性验证:如机械耦合器需通过动态载荷测试以满足防爆结构要求。
二、TM 5-855-02的爆炸压力效应研究方法
1. 数据驱动方法
- 经验公式推导:基于大量爆炸试验数据拟合参数,如自由场正压持续时间的经验公式。
- TNT当量法:将非球形装药等效为球形TNT,简化爆炸效应的计算。
- 数值模拟验证:结合有限元分析(如ABAQUS的CONWEP模块)模拟爆炸波传播,并与实验数据对比。
2. 实验数据采集
- 传感器布置:使用高灵敏度压力传感器记录压力时程曲线,重点关注峰值超压和冲量。
- 动态应变率测试:评估材料在高应变率下的力学性能,如BFRP筋混凝土板的抗爆试验。
三、UFC 3-340-02与TM 5-855-02的异同点
| 对比维度 | UFC 3-340-02 | TM 5-855-02 |
|---|---|---|
| 核心目标 | 结构抗爆设计与安全评估 | 爆炸压力效应参数的理论推导与实验验证 |
| 参数侧重点 | 结构响应(层裂、冲量、泄漏压力) | 自由场爆炸参数(超压、冲量、传播速度) |
| 方法学 | 动态载荷等效静力法、有限元分析 | 经验公式、TNT当量法、实验数据拟合 |
| 应用场景 | 军事设施、化工建筑防护设计 | 地面结构抗恐怖袭击设计、爆炸危害评估 |
| 协同关系 | 引用TM的参数计算结果进行结构分析 | 提供UFC所需的基础爆炸数据 |
四、实验数据获取方法
1. 规范指导的实验设计
- 爆炸参数测量:按UFC 3-340-02的图表布置测点(如不同方位角和爆距),记录压力时程曲线(图7)。
- 密闭空间模拟:采用双三角形载荷模型,通过压力传感器测量冲击波和准静态气压的联合作用。
2. 数值模拟与验证
- 有限元建模:使用CONWEP或LS-DYNA模拟爆炸波传播,验证与UFC图表的一致性(图8)。
- 参数敏感性分析:调整装药形状、爆距和环境条件,研究对超压和冲量的影响。
3. 动态材料测试
- 高应变率试验:通过霍普金森杆测试混凝土和复合材料的动态强度,补充规范中的静态参数。
五、总结与展望
UFC 3-340-02与TM 5-855-02共同构成了爆炸效应研究的核心框架:前者提供结构设计准则,后者支撑参数计算。未来方向包括:
- 多物理场耦合:结合热-力-化学耦合效应,提升近场爆炸模拟精度。
- 新材料适用性:验证FRC等新型材料的抗爆性能,修订现有层裂预测模型。
- 智能化工具开发:基于机器学习优化爆炸参数预测,如超高韧性水泥基板的损伤预测。
通过整合实验、模拟和规范,可显著提升抗爆结构的安全性和经济性。
📚2 运行结果
FAB = matfile('FreeAirBurstParametersPositivePhaseMetric.mat');
figure; hold on; box on; grid on;
title({'Positive phase shock wave parameters for a spherical';...
'TNT explosion in free air at sea level'})
xlabel('Scaled Distance Z = R/W^{1/3} [m/kg^{1/3}]')
axis([0.05 50 0.005 1e6])
plot(FAB.ScaledDistance1 ,FAB.ReflectedPressure)
plot(FAB.ScaledDistance2 ,FAB.PeakIncidentOverpressure)
plot(FAB.ScaledDistance3 ,FAB.ScaledReflectedImpuls)
plot(FAB.ScaledDistance4 ,FAB.ScaledIncidentImpuls)
plot(FAB.ScaledDistance5 ,FAB.ScaledArivalTime)
plot(FAB.ScaledDistance6 ,FAB.ScaledPositivePhaseDuration)
plot(FAB.ScaledDistance7 ,FAB.WaveFrontSpeed)
plot(FAB.ScaledDistance8 ,FAB.ScaledWaveLength)
set(gca,'yscale','log');
set(gca,'xscale','log');
legend('P_r, kPa','P_{so}, kPa','i_r/W^{1/3}, kPa-ms/kg^{1/3}','i_s/W^{1/3}, kPa-ms/kg^{1/3}',...
't_a/W^{1/3}, ms/kg^{1/3}','t_0/W^{1/3}, ms/kg^{1/3}','U, m/ms','L_w/W^{1/3}, m/kg^{1/3}')
HSB = matfile('HemisphericalBurstParametersPositivePhaseMetric.mat');
figure; hold on; box on; grid on;
title({'Positive phase shock wave parameters for a hemispherical';...
'TNT surface explosion at sea level'})
xlabel('Scaled Distance Z = R/W^{1/3} [m/kg^{1/3}]')
axis([0.05 50 0.005 1e6])
plot(HSB.ScaledDistance1 ,HSB.ReflectedPressure)
plot(HSB.ScaledDistance2 ,HSB.PeakIncidentOverpressure)
plot(HSB.ScaledDistance3 ,HSB.ScaledReflectedImpuls)
plot(HSB.ScaledDistance4 ,HSB.ScaledIncidentImpuls)
plot(HSB.ScaledDistance5 ,HSB.ScaledArivalTime)
plot(HSB.ScaledDistance6 ,HSB.ScaledPositivePhaseDuration)
plot(HSB.ScaledDistance7 ,HSB.WaveFrontSpeed)
plot(HSB.ScaledDistance8 ,HSB.ScaledWaveLength)
set(gca,'yscale','log');
set(gca,'xscale','log');
legend('P_r, kPa','P_{so}, kPa','i_r/W^{1/3}, kPa-ms/kg^{1/3}','i_s/W^{1/3}, kPa-ms/kg^{1/3}',...
't_a/W^{1/3}, ms/kg^{1/3}','t_0/W^{1/3}, ms/kg^{1/3}','U, m/ms','L_w/W^{1/3}, m/kg^{1/3}')
RPC = matfile('ReflectedPressureCoefficientVsAngleOfIncidenceMetric.mat');
figure; hold on; box on; grid on;
title('Reflected Pressure Coefficient')
view(3)
surf(RPC.AngleIncrements, RPC.PressureIncrements,RPC.AngleOfInclanationCoeficientMatrix)
xlabel('angle [deg]')
ylabel('Peak incident overpressure [kPa]')
zlabel('C_{r \alpha} = {P_r \alpha} / P_{SO}')
set(gca,'yscale','log');
% or as a line plot
figure; hold on; box on; grid on;
plot(RPC.AngleIncrements,RPC.AngleOfInclanationCoeficientMatrix)
title('Reflected Pressure Coefficient')
xlabel('angle [deg]')
ylabel('C_{r \alpha} = {P_r \alpha} / P_{SO}')
RSI = matfile('ReflectedScaledImpulseVsAngleOfIncidenceMetric.mat');
figure; hold on; box on; grid on;
title('Reflected Scaled Impulse')
view(3)
surf(RSI.AngleIncrements, RSI.PressureIncrements,RSI.ReflectedScaledImpulseMatrix)
xlabel('angle [deg]')
ylabel('Peak incident overpressure [kPa]')
zlabel('i_{r \alpha} / W^{1/3} [kPa-msec/kg^{1/3}]')
set(gca,'yscale','log');
set(gca,'zscale','log');
% or as a line plot
figure; hold on; box on; grid on;
plot(RSI.AngleIncrements, RSI.ReflectedScaledImpulseMatrix)
title('Reflected Scaled Impulse')
xlabel('angle [deg]')
ylabel('i_{r \alpha} / W^{1/3} [kPa-msec/kg^{1/3}]')
set(gca,'yscale','log');
MSH = matfile('MachStemHightMetric.mat');
figure; hold on; box on; grid on; grid minor
title('Scaled height of triple point')
xlabel('Scaled Horizontal Distance from Charge, m/kg^{1/3}')
ylabel('Scaled Height of Triple Point, H_{T}/W{^1/3} (m/kg^{1/3})')
axis([0 9 0 5])
plot(MSH.ScaledHorizontalDistanceMatrix', MSH.ScaledTriplePointHightMatrix','k')
text(MSH.ScaledHorizontalDistanceMatrix(:,end),MSH.ScaledTriplePointHightMatrix(:,end),...
num2str(round(MSH.ScaledChargeHight',3)))
str1 = {'Number adjacent to curves','indicate scaled charge','height, H_c/W^{1/3}'};
text(8.8, 4.8, str1, 'HorizontalAlignment', 'right', 'VerticalAlignment', 'top',...
'EdgeColor', 'k', 'Margin', 1.5, 'LineWidth', 1,'BackgroundColor','w')
figure; hold on; box on; grid on;
title('Angular reflected pressure')
xlabel('Horisonal distance form charge [m]')
ylabel('Pressure [kPa]')
plot(X,Pra_line) 
figure; hold on; box on; axis equal;
colormap jet
ylabel(colorbar,'Pressure [kPa]')
xlabel('Distance from center [m]')
ylabel('Distance from center [m]')
title('Angular reflected pressure')
contourf(X,flipud(Y'),Pra_contour) 
W = 0.9; % [kg] Charge
R = 2.5; % [m] Distance
Type = 'Surface'; % Detonation type
[Pr, Pso, ir, is, ta, to, U, Lw, Z] = BlastParameters(R, W, Type);
b = DecayCoefficient(Pso,is,to); % Decay coefficient for the Friedlander's equation
t = linspace(0,to,25); % [ms]
Ps = FriedlandersEquation(Pso, to, b, t);
figure; hold on; box on; grid on;
title('Incident overpressure history')
xlabel('Time, ta = 0, [ms]')
ylabel('Pressure [kPa]')
plot(t,Ps)
部分代码:
function Ps = FriedlandersEquationReal(Pso, ta, to, b, t)
%FriedlandersEquationReal Determines the pressure at time t following the
%Friedlander's equation for blast waveform.
%Ps = FriedlandersEquationReal(Pso, ta, to, b, t)
% INPUT
% Pso [kPa] Peak overpressure
% to [ms] Positive phase duration
% b [-] Decay coefficient for the waveform
% t [ms] Time 0 < t < ta+to (zero is time of detonation)
%
% OUTPUT
% Ps [kPa] Overpressure at time t
%
% The Friedlander's equation is given in the form of:
% Ps(t) = Pso*(1-(t-ta)/to)*exp(-b*(t-ta)/to)
%
% The units are only recommendations and may be changed at own risk.
% The start time, ta, is NOT set to zero.
% Determine the pressure at time t
Ps = Pso*(1-(t-ta)./to).*exp(-b*(t-ta)./to);
% Correct time for special cases
Ps(t<ta) = 0;
Ps(t>(ta+to)) = 0;
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
[1] Lawver D , Weeks J , Forman S ,et al.Cost Savings Using Stirrup Reinforcement Instead of Laced Wall Reinforcement Per UFC 3-340-02 (TM 5-1300) December, 2008[J]. 2010.
[2] Jr W H Z , Acosta P F .SUMMARY OF THE NEW REINFORCED CONCRETE BLAST DESIGN PROVISIONS IN UFC 3-340-02, 'STRUCTURES TO RESIST THE EFFECTS OF ACCIDENTAL EXPLOSIONS'[C]//ACI Fall convention.DoD Explosives Safety Board in Alexandria, Virginia; US Army Engineering and Support Center, Huntsville, 2010.
[3]彭琦,吴昊,方秦,等.长持时平面爆炸波作用下RC梁动力响应研究[J].建筑结构学报, 2023, 44(3):15.




















 818
818

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








