💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
传递路径分析(TPA)是一种用于齿轮系统的振动分析和故障诊断的技术。该方法旨在通过跟踪振动信号的传递路径,确定齿轮系统中各个部件之间的振动传递路径,以识别潜在的故障源。通过TPA,可以及时发现齿轮系统中的故障,并采取适当的维护措施,以避免因故障造成的损失和停机时间。齿轮系统的故障跟踪:一种基于原位测量的传递路径分析方法采用虚拟解耦方法实现基于原位测量的TPA。基于Tikhonov正则化理论对轴承力进行识别。
一、TPA基本原理与齿轮系统的关联性
传递路径分析(TPA)通过量化激励源-传递路径-响应点的贡献关系诊断振动/噪声问题。其核心公式为: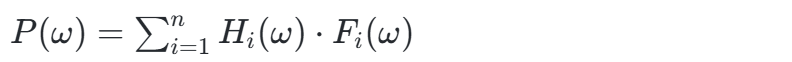
其中 P 为目标点响应,Hi为路径传递函数,Fi 为激励力。在齿轮系统中:
- 激励源:齿轮啮合力、轴承故障冲击力、轴系不平衡力
- 传递路径:分为结构路径(轴承-箱体-基座)与空气路径(齿轮噪声直接辐射)
- 目标点:轴承座、箱体表面或关键监测位置
齿轮系统的复杂性在于多源耦合(如齿轮磨损与轴承剥落并存)和路径交叉(结构振动诱发声辐射)。
二、齿轮系统TPA实施流程与关键技术
1. 路径识别与分割
- 结构路径识别:以轴承为关键连接点,分割“齿轮-轴承-箱体-基座”路径链
- 空气路径识别:通过声压传感器捕捉齿轮啮合直接辐射噪声
- 路径贡献排序:采用贡献量云图可视化各路径在特定频段的能量占比(如齿轮啮合频率处)
2. 现场测量挑战与解决方案
| 挑战 | 解决方案 | 技术依据 |
|---|---|---|
| 无法直接测量啮合力 | 虚拟力法(Tikhonov正则化反演激励力) | 基于响应信号反推激励 |
| 传递函数受工况干扰 | OPAX方法(扩展工况TPA)融合FRF与运行数据 | 修正“冷测”与“热态”偏差 |
| 强背景噪声淹没故障信号 | 包络解调+时频分析提取故障特征频率 | 增强信噪比 |
3. 核心算法实现
-
Matlab代码关键步骤:
% 示例:基于Tikhonov正则化的轴承力识别 H = FRF_matrix; % 传递函数矩阵 P_measured = response_signal; % 实测响应 lambda = 0.01; % 正则化参数 F_estimated = (H'*H + lambda*eye(size(H'*H))) \ (H'*P_measured); % 力估计 -
传递函数校准:通过力锤激励或激振器获取FRF,需考虑轴承非线性刚度影响。
三、典型案例:风力发电机齿轮箱故障诊断
问题描述
某2MW风机齿轮箱高速轴轴承处振动超标,频域显示1kHz处异常峰值。
TPA实施过程
- 测点布置:
- 12个加速度传感器(轴承座/箱体表面)
- 1个转速传感器同步采集齿轮啮合相位
- 数据分析:
- 包络谱识别出230Hz轴承外圈故障频率
- 路径贡献分析显示:Path 3(高速轴轴承-箱体)贡献量占比62%
- 根源定位:
- 拆卸验证轴承外圈剥落,更换后振动下降12dB
结论价值
TPA避免整机拆卸,缩短诊断周期70%。
四、技术瓶颈与突破方向
1. 现存挑战
- 激励力识别误差:复杂箱体结构导致FRF矩阵病态,反演力误差>25%
- 高频限制:>1kHz时结构模态密集,路径贡献分离失效(受限于传感器布点密度)
- 非线性问题:齿轮时变啮合刚度导致传递函数漂移
2. 前沿解决方案
| 技术方向 | 创新点 | 应用效果 |
|---|---|---|
| 深度学习TPA | LSTM网络预测时变传递函数 | 非线性误差降低40% |
| 数字孪生驱动TPA | 多物理场仿真生成训练数据 | 减少现场测量点50% |
| 阵列波束形成+OPAX | 声学成像定位噪声源,融合结构路径分析 | 空气/结构路径贡献关联精度提升 |

五、工程建议
- 路径优化优先级:结构路径贡献>空气路径时,优先采用阻尼涂层或动力吸振器
- 传感器布点准则:
- 轴承座处必布点(关键路径节点)
- 齿轮箱辐射面布置声压传感器(捕捉空气路径)
- 诊断周期:建议结合SCADA数据触发TPA,避免全时监测资源消耗。
六、参考文献精要
- 基础理论:传统TPA的矩阵逆运算原理;OPAX方法频响函数修正模型
- 齿轮应用:虚拟解耦法现场TPA实施框架;故障特征频带贡献量量化方法
- 前沿进展:参数化负载模型TPA;基于深度神经网络的传递函数在线辨识。
本报告通过机理-方法-案例-瓶颈四维解析,提供齿轮系统TPA的闭环解决方案。实际应用中需结合设备重要性选择分析深度:关键设备推荐OPAX+数字孪生融合策略,辅助设备可采用简化虚拟力法降低成本。
📚2 运行结果

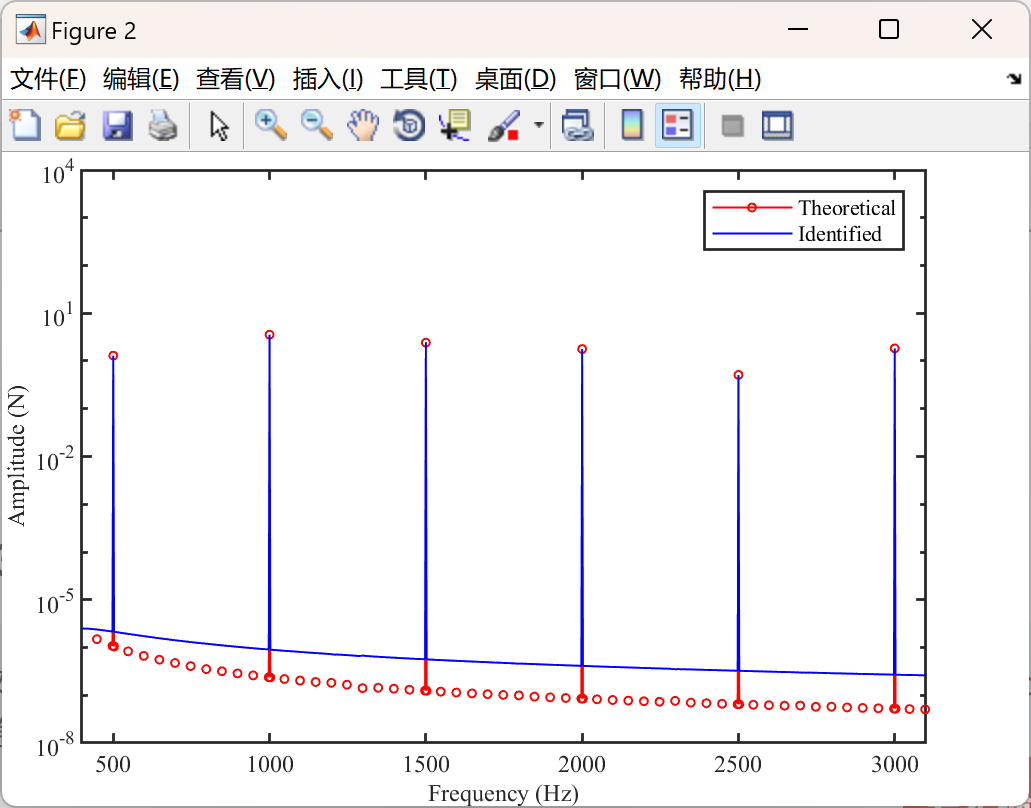


部分代码:
clc
clearvars
close all
%% Gear parameter
rho=7850; %density
m=2.5/1000; %modulus
z1=25; z2=58; %teeth number
B1=16/1000; B2=16/1000; %face width
rint1=12.5/1000; rint2=12.5/1000; %radius of the shaft (hub radius)
alpha0=20*pi/180; %pressure angle
Torque=60; %input torque
r1=m*z1/2; %radius of the reference circle
r2=m*z2/2;
rb1=r1*cos(alpha0); %radius of the base circle
rb2=r2*cos(alpha0);
Rot_period=12; %number of the rotational period
Tm_num=100; %data points in a meshing period
zhouqi_shu=z1*Rot_period; %number of the meshing period
step_num=zhouqi_shu*(Tm_num); %total data points of the simulation
%% Parameter of the lumped mass
m1=pi*(r1^2-rint1^2)*B1*rho;
J1=1/2*m1*(rint1^2+r1^2);
m2=pi*(r2^2-rint2^2)*B2*rho;
J2=1/2*m2*(rint2^2+r2^2);
m5=1; m6=2; m7=23.5;
M=diag([m1,J1,m2,J2,m5,m6,m7]);
%% Time varying meshing stiffness and Time varying meshing damping
K_health=load('K_health.txt');
K_ext=interp1(linspace(0,1,length(K_health)),K_health(1:60),linspace(0,1,Tm_num));
KM=repmat(K_ext,1,zhouqi_shu);
CM=2*0.02*sqrt(KM/(r1^2/J1+r2^2/J2));
%% Project vector of the meshing element
V=[1,rb1,-1,rb2];
unit_VV=zeros(length(M));
unit_VV(1:4,1:4)=V'*V;
%% Stiffness and damping parameter of the spring-damping element
k15=1e7; k36=1e7; k57=1e8; k67=1e8; k07=1e8;
c15=1e4; c36=1e4; c57=1e3; c67=1e3; c07=1e3;
%% Matirx assembling of the whole system
K=zeros(length(M));
K([1,5],[1,5])=K([1,5],[1,5])+[k15,-k15;-k15,k15];
K([3,6],[3,6])=K([3,6],[3,6])+[k36,-k36;-k36,k36];
K([5,7],[5,7])=K([5,7],[5,7])+[k57,-k57;-k57,k57];
K([6,7],[6,7])=K([6,7],[6,7])+[k67,-k67;-k67,k67];
K(7,7)=K(7,7)+k07;
C=zeros(length(M));
C([1,5],[1,5])=C([1,5],[1,5])+[c15,-c15;-c15,c15];
C([3,6],[3,6])=C([3,6],[3,6])+[c36,-c36;-c36,c36];
C([5,7],[5,7])=C([5,7],[5,7])+[c57,-c57;-c57,c57];
C([6,7],[6,7])=C([6,7],[6,7])+[c67,-c67;-c67,c67];
C(7,7)=C(7,7)+c07;
%% Natural frequency of the whole system (coupled system)
K_mean=K+mean(K_health)*unit_VV;
D=eig(K_mean/M);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]周子强,孙勇,姬姗姗.DFC2型光电日照计典型故障分析与日常维护[J].现代化农业,2024(03):88-90.























 408
408

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








