【多元回归】使用多种核函数的核岭回归（Matlab实现）

原创于 2025-05-07 18:39:38 发布 · 943 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#回归 #数据挖掘 #人工智能

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

引言

在机器学习的回归分析任务中，如何准确捕捉数据的非线性关系，同时避免模型过拟合，始终是研究与应用的关键难题。传统线性回归方法在处理复杂非线性数据时往往力不从心，而单一核函数的核岭回归虽能借助核技巧将数据映射到高维空间以处理非线性问题，但由于不同核函数对数据特征的挖掘能力各有侧重，单一核函数难以适配所有类型的数据分布。在此背景下，使用多种核函数的核岭回归应运而生，它通过融合不同核函数的优势，为解决复杂回归问题提供了更强大、灵活的方案，在数据科学、工程技术、生物医学等众多领域展现出巨大的应用潜力。

原理

核岭回归本质上是岭回归与核方法的结合。岭回归是在线性回归的损失函数中引入 L2 正则化项，通过约束回归系数的大小，降低模型复杂度，防止过拟合，其优化目标是最小化经验风险与正则化项之和。而核方法的核心思想是利用核函数将原始低维空间中的非线性数据映射到高维空间，使得在高维空间中数据能够通过线性模型进行处理，避免了直接在高维空间进行复杂的计算。核岭回归将两者结合，在高维特征空间中执行岭回归操作，通过求解带有正则化项的优化问题，找到最优的回归函数。

当引入多种核函数时，核岭回归进入多核学习（Multiple Kernel Learning，MKL）框架。在多核学习中，不同的核函数从不同角度刻画数据点之间的相似性。例如，线性核函数能够描述数据的线性关系，计算效率高；径向基函数（RBF）核对非线性数据有很强的拟合能力，可灵活适应各种数据分布；多项式核函数则擅长捕捉数据的多项式特征。多种核函数通过加权组合的方式，形成一个复合核函数，每个核函数的权重反映了其对最终模型的贡献程度。模型训练过程不仅要学习回归系数，还要优化各个核函数的权重，以实现对数据的最佳拟合。这一过程通常基于优化算法，如梯度下降法、交替优化法等，通过不断调整参数，最小化目标函数，从而确定最优的核函数组合与回归模型。

优势

使用多种核函数的核岭回归具有显著优势。其一，强大的非线性拟合能力，通过融合不同核函数，模型能够从多个维度挖掘数据特征，更全面地捕捉数据的非线性关系，在处理复杂数据分布时表现出色；其二，良好的泛化性能，正则化项的存在以及多核的协同作用，有效控制了模型复杂度，增强了模型对噪声和异常值的鲁棒性，降低过拟合风险，提升泛化能力；其三，高度的灵活性，用户可根据数据特点和问题需求，自由选择和组合核函数，定制适合特定任务的模型，极大地拓展了模型的应用范围。

局限

尽管该方法优势突出，但也存在一定局限性。一方面，模型复杂度显著增加，多种核函数的引入使得参数空间变得庞大，不仅需要确定每个核函数自身的参数，还要优化核函数之间的权重，这导致参数调优难度大幅提升，往往需要大量的计算资源和时间进行交叉验证等操作；另一方面，计算效率较低，在处理大规模数据时，核岭回归本身的计算复杂度较高，而多核学习进一步加剧了这一问题，随着数据量和核函数数量的增加，内存需求和计算时间呈指数级增长，限制了其在实时性要求高的场景中的应用。

应用

使用多种核函数的核岭回归在众多领域已得到广泛应用。在生物信息学中，可用于蛋白质结构预测、基因表达分析等，通过多核融合挖掘生物数据的复杂特征；在金融领域，适用于股票价格预测、信用风险评估，帮助分析金融市场的复杂波动；在图像与信号处理领域，能够对图像特征、信号模式进行回归分析，实现图像识别、信号降噪等功能。随着技术的发展，该方法有望在更多领域发挥更大作用，推动各行业的数据分析与预测能力迈向新台阶。

📚2 运行结果

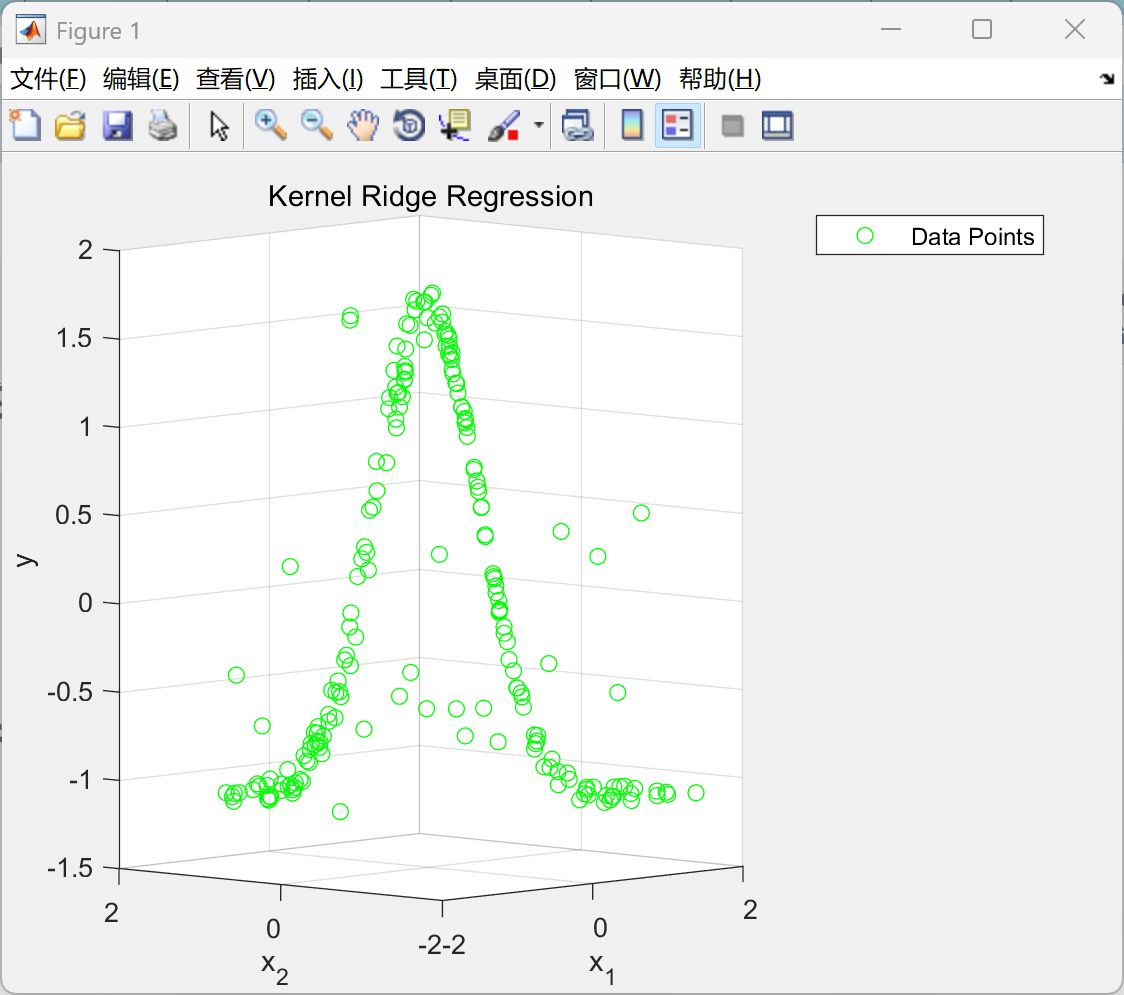
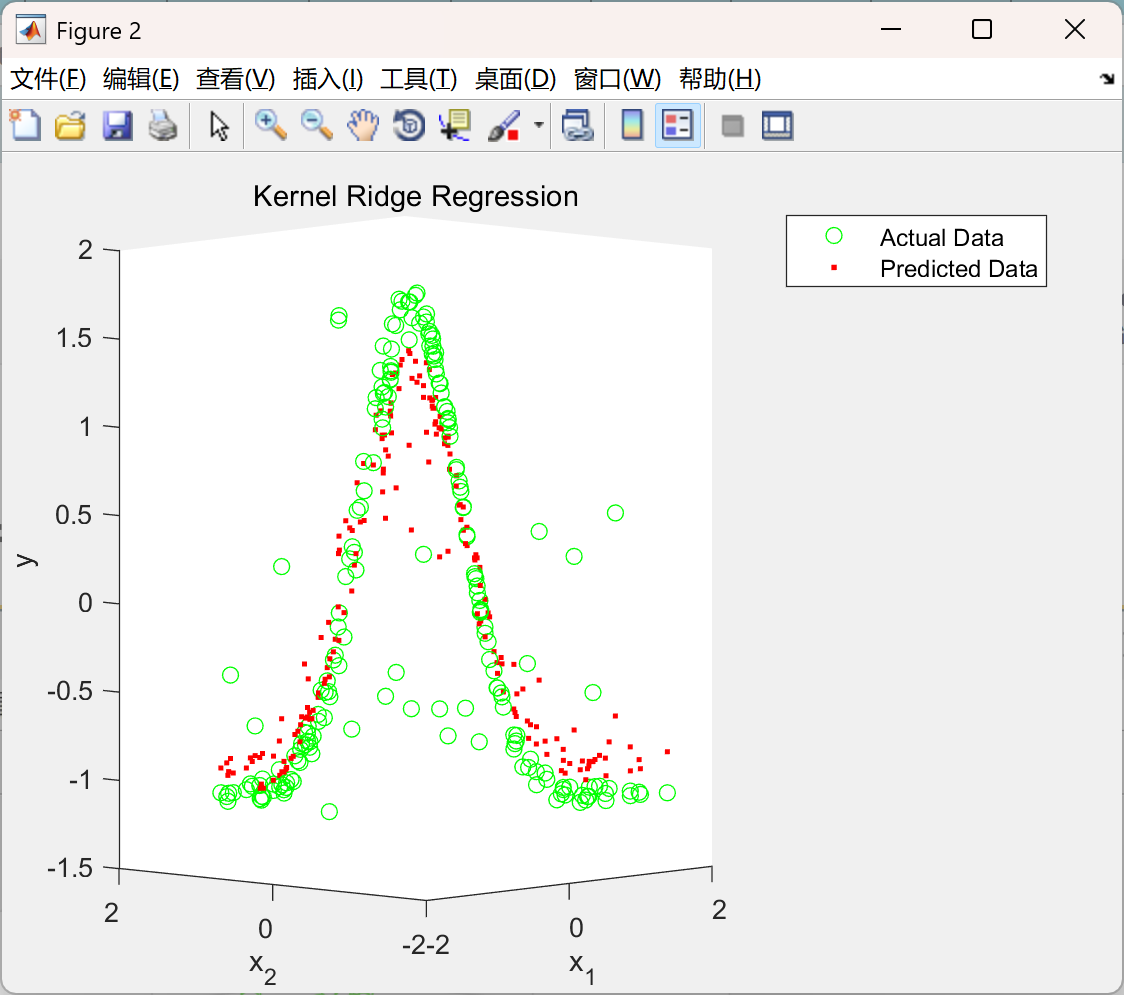
部分代码：


% Initailization (Dataset: data2)
clear all;clc;
 
% * Zscore normalization

data=zscore(csvread('GaussianData.csv'));
x=data(:,1:end-1);
y=data(:,end);
% 
% * Total number of data points

N=length(data);
% 
% * Visualization of the Data

figure
scatter3(x(:,1),x(:,2),y,'g')
title('Kernel Ridge Regression')
xlabel({'x_1'})
ylabel({'x_2'})
zlabel('y')
view([-47.1 4.4])
legend('Data Points')
% Various Kernels for above data
% * Linear Kernel
%
K_linear=(x*x');
% 
% * Polynomial Kernel (Poly3)

K_poly3=(x*x').^3;
% 
% * Gaussian Kernel

K_gauss=zeros(N,N);
for j=1:N
 for i=1:N
    K_gauss(i,j)=exp(-norm(x(j,:)-x(i,:)));
 end
end
% Algorithm
% # f_linear : Regression Function due to Linear Kernel
% # f_poly3 : Regression Function due to Poly3 Kernel
% # f_gaussian : Regression Function due to Gaussian Kernel
% 
% * mse : Mean Square Error
% * A\b instead of inv(A)*b for faster computation
%
f_linear=zeros(N,1);
f_poly3=zeros(N,1);
f_gaussian=zeros(N,1);

mse=[];
intvl=0.1;

for lambda=intvl:intvl:1
    
    for i=1:N
        
        f_linear(i,1)= y'*((K_linear+ lambda*eye(N))\K_linear(i,:)');
        
        f_poly3(i,1)= y'*((K_poly3+ lambda*eye(N))\K_poly3(i,:)');
        
        f_gaussian(i,1)= y'*((K_gauss+ lambda*eye(N))\K_gauss(i,:)');
    end
     
    mse=[mse; norm(f_linear-y)^2/N, norm(f_poly3-y)^2/N, norm(f_gaussian-y)^2/N];
end
% Mean square error is the assessment measure for optimal Kernel
%
mse_=min(mse(:,1));
fprintf('Mean square error (Linear Kernel) : %f',mse_)

mse_=min(mse(:,2));
fprintf('Mean square error (Poly3 Kernel) : %f',mse_)

[mse_,gaussain_indx]=min(mse(:,3));
fprintf('"minimum" Mean square error (Gaussian Kernel) : %f',mse_)

% Optimal Langrangian Parameter
%
lambda_optimal=intvl*gaussain_indx
% Prediction Values (due to various Kernels)
%
Predicted=[y,f_linear,f_poly3,f_gaussian]
% Alpha & Dual, calculated as follows :
%
alpha=2*lambda_optimal*inv((K_gauss+lambda_optimal*eye(N)))*y
W_alpha=y'*alpha -(1/4*lambda_optimal)*alpha'*K_gauss*alpha -(1/4)*alpha'*alpha
% Actual Vs Predicted Values
%
figure
hold on

scatter3(x(:,1),x(:,2),y,'g')
scatter3(x(:,1),x(:,2),f_gaussian,'.r')

title('Kernel Ridge Regression')
xlabel({'x_1'})
ylabel({'x_2'})
zlabel('y')
view([-47.1 4.4])
legend('Actual Data','Predicted Data')