支持向量回归（Matlab实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

在机器学习的回归分析领域，支持向量回归（Support Vector Regression，简称 SVR）是一种基于支持向量机（SVM）理论发展而来的重要算法，以其独特的优化策略和出色的泛化能力，在处理复杂回归问题时展现出显著优势，被广泛应用于众多学科与工程领域。

SVR 的核心原理基于结构风险最小化原则，旨在寻找一个最优超平面，使得样本点到该超平面的误差尽可能小。与传统回归方法追求预测值与真实值完全匹配不同，SVR 引入了 “ε - 不敏感带” 的概念。在这个误差带内，模型不计算误差，只有当预测值与真实值的偏差超出该误差带时，才会计算损失并进行优化。通过这种方式，SVR 对噪声和异常值具有更强的鲁棒性，能够有效避免过拟合现象。在实际计算中，SVR 通过引入松弛变量来允许部分样本点偏离误差带，同时通过惩罚因子 C 平衡模型的拟合精度与泛化能力。C 值越大，对误差的容忍度越低，模型越倾向于拟合训练数据；C 值越小，则模型的泛化能力越强。

核函数是 SVR 的另一个关键要素。SVR 通过核函数将低维空间中的非线性数据映射到高维空间，在高维空间中寻找线性回归超平面，从而巧妙地解决了非线性回归问题。常见的核函数包括线性核、多项式核、径向基函数（RBF）核和 Sigmoid 核等。不同的核函数具有不同的特性，适用于不同类型的数据分布。例如，RBF 核函数能够灵活地处理各种非线性关系，在实际应用中最为广泛；而线性核函数则适用于数据本身线性可分或近似线性可分的情况，计算效率更高。

支持向量回归具有诸多显著特点。其一，它在小样本数据的回归任务中表现出色，凭借其强大的非线性映射能力，能够从少量数据中挖掘出潜在规律，实现精准预测；其二，SVR 能够提供全局最优解，这得益于其基于凸优化的求解过程，避免了陷入局部最优的问题；其三，SVR 对高维数据具有良好的适应性，核函数的使用使其无需在高维空间中显式地计算数据映射，降低了计算复杂度。

在实际应用场景中，SVR 发挥着重要作用。在金融领域，可用于股票价格预测、风险评估等，帮助投资者制定决策；在工业生产中，能够对产品质量进行预测和控制，优化生产流程；在环境科学领域，可用于污染物浓度预测、气候变化分析等，为环境保护提供数据支持。

不过，SVR 也存在一定的局限性。一方面，它对核函数和参数（如 C 和 ε）的选择极为敏感，不同的参数设置会导致模型性能出现较大差异，而寻找最优参数往往需要耗费大量的时间和计算资源进行交叉验证；另一方面，在处理大规模数据时，SVR 的计算效率较低，训练时间长，限制了其在实时性要求较高场景中的应用。

综上所述，支持向量回归凭借独特的理论基础和优良的性能，成为回归分析中的重要工具。尽管存在参数选择和计算效率等方面的挑战，但随着技术的不断发展，如结合分布式计算、改进参数优化算法等，SVR 有望在更多领域发挥更大的价值，为复杂回归问题提供更高效、准确的解决方案。

📚2 运行结果

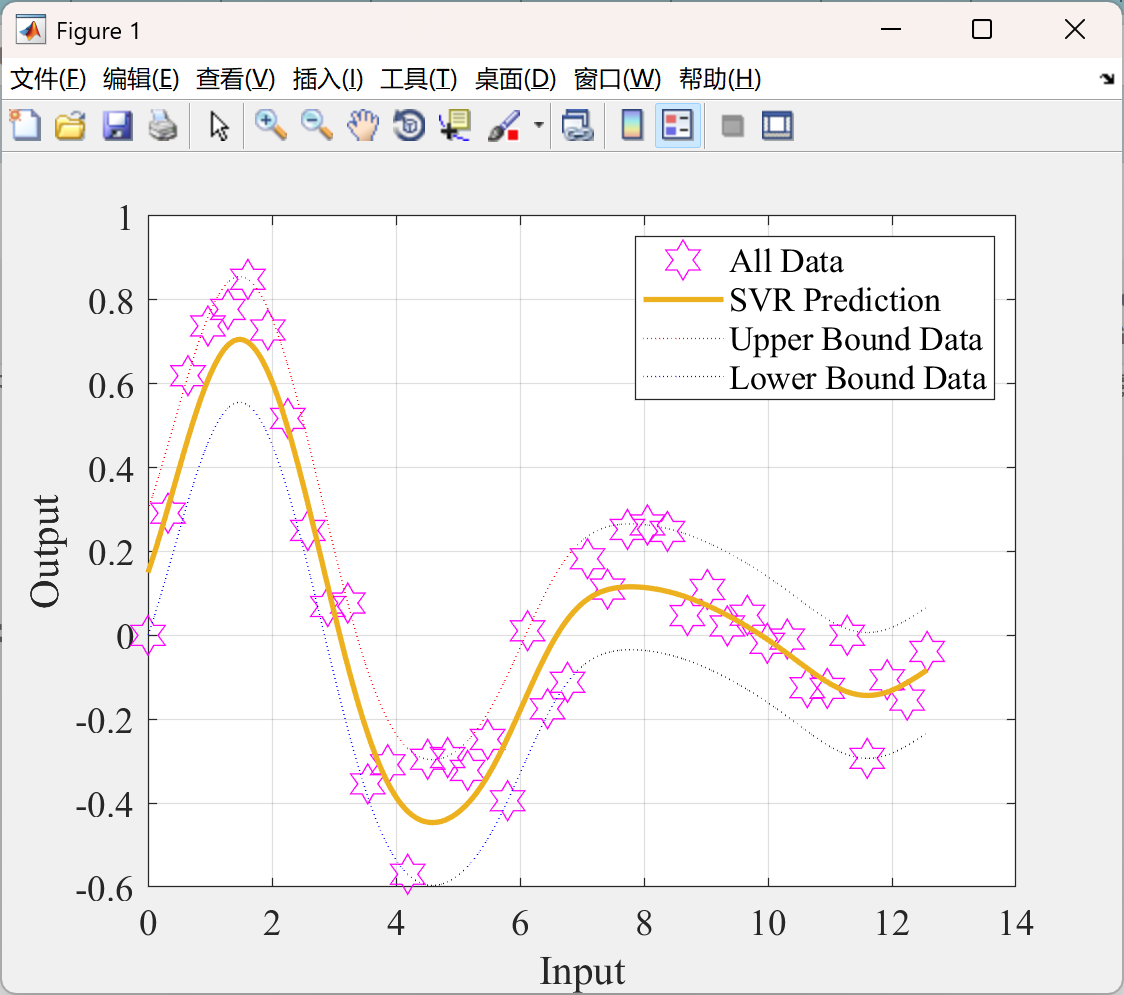
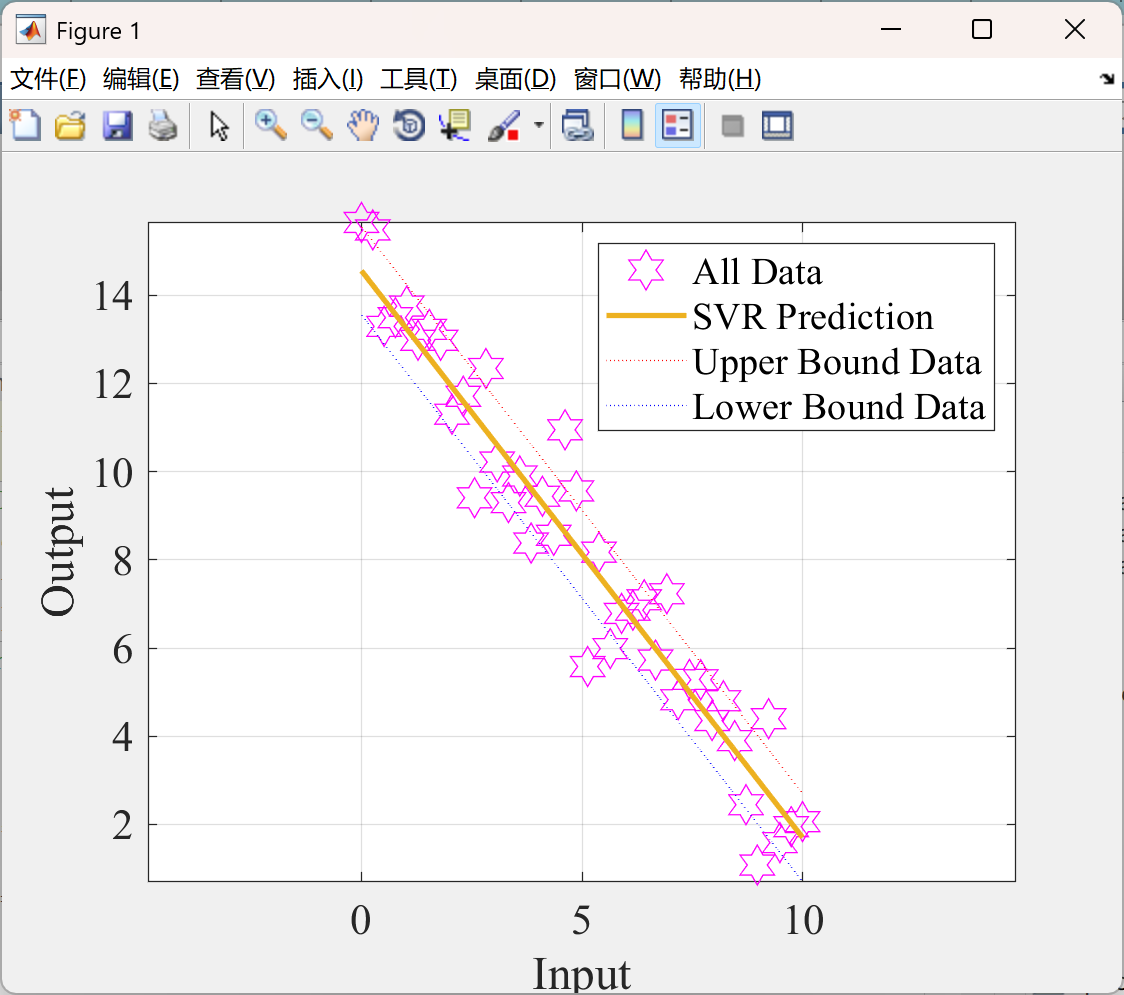
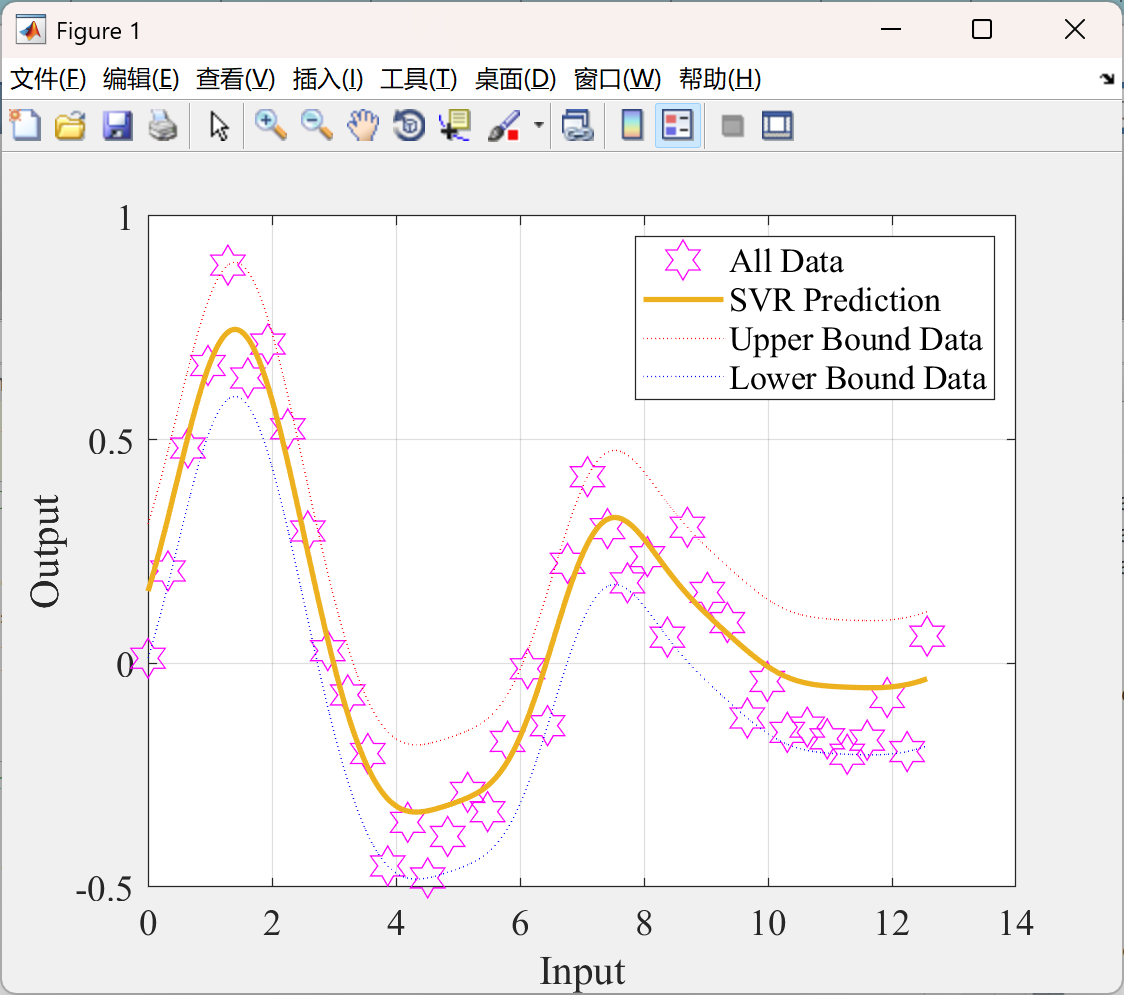
部分代码：

clc,clear,close all;

%% Load Data
x=linspace(0,10,40);
t=-1.35*x+15+1*randn(size(x)); 
n=numel(t);
%% Design Support Vector Regression
epsilon=1;
C=1;

H=zeros(n,n);
for i=1:n
    for j=i:n
        H(i,j)=x(:,i)'*x(:,j);
        H(j,i)=H(i,j);
    end
end
HH=[ H -H
    -H  H];
f=[-t'; t']+epsilon;
Aeq=[ones(1,n) -ones(1,n)];
beq=0;
lb=zeros(2*n,1);
ub=C*ones(2*n,1);
options=optimset('Display','iter','MaxIter',1000);

%% Calculating Support Vectors 
alpha=quadprog(HH,f,[],[],Aeq,beq,lb,ub,[],options);
alpha=alpha';

%% Set zero for very negative ones
Setzero=(abs(alpha)<max(abs(alpha))*1e-4);

alpha(Setzero)=0;
alpha_plus=alpha(1:n);
alpha_minus=alpha(n+1:end);

eta=alpha_plus-alpha_minus;
S=find(alpha_plus+alpha_minus>0 & alpha_plus+alpha_minus<C);

w=0;
for i=1:n
    w=w+eta(i)*x(:,i);
end

b=mean(t(S)-w'*x(:,S)-sign(eta(S))*epsilon);

%% Plot Results
figure;
p=plot(x,t,'hexagram');
p.Color = "magenta";
p.MarkerSize = 15;
hold on;
xmin=min(x);
xmax=max(x);
xx=linspace(xmin,xmax,500);
yy=w'*xx+b;
plot(xx,yy,'Color',[0.9290 0.6940 0.1250],'LineWidth',2);
plot(xx,yy+epsilon,'r:');
plot(xx,yy-epsilon,'b:');
legend('All Data', 'SVR Prediction','Upper Bound Data', 'Lower Bound Data');
xlabel('Input');
ylabel('Output');
set(gca,'fontname','Times New Roman','FontSize', 16);  % Set fontname

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]谢波,程玉峰,谭冬维,等.基于支持向量机原理的高填方路基施工期沉降预测[J/OL].路基工程,1-7[2025-05-07].https://doi.org/10.13379/j.issn.1003-8825.202408042.

[2]Li S ,Yang X ,Ren H , et al.Non-parametric identification modeling and prediction of intelligent ship maneuvering motion based on real ship test at sea[J].Ocean Engineering,2025,330121267-121267.

🌈4 Matlab代码实现