2025超新算法/植物水分吸收与运输算法（Matlab实现）

荧光Matlab

已于 2025-05-08 21:51:50 修改

阅读量1.7k

点赞数 8

CC 4.0 BY-SA版权

文章标签：算法

于 2025-05-08 17:40:13 首次发布

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/147798484

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

基本介绍

植物水分吸收与运输是植物生命活动的基础过程，它维系着植物的生长、发育与生存，同时也在全球生态系统的物质循环和能量流动中扮演关键角色。为了深入理解、精确模拟和有效调控这一复杂过程，植物水分吸收与运输算法应运而生。这些算法基于数学模型与计算机技术，将植物生理学、土壤学、气象学等多学科知识进行整合，旨在揭示植物水分吸收与运输的内在机制，预测其在不同环境条件下的动态变化。在农业生产中，此类算法可助力优化灌溉策略，提高水资源利用效率；在生态研究领域，能够帮助评估生态系统对气候变化的响应，为植被恢复和生态保护提供科学依据；在林业管理方面，可辅助分析树木水分状况，保障森林健康。因此，植物水分吸收与运输算法的研究与应用具有重要的理论意义和实践价值。

原理

1. 土壤 - 植物 - 大气连续体（SPAC）理论

植物水分吸收与运输算法的核心理论基础是 SPAC 理论，该理论将土壤、植物和大气视为一个连续的水分传输系统。在这个系统中，水分遵循能量守恒和热力学定律进行运动，其驱动力源于水势差。土壤水势反映了土壤中水分的能量状态，受到土壤质地、含水量、溶质浓度等因素影响；植物水势则由根系、茎干和叶片等部位的水势组成，其中根系水势对水分吸收起关键作用。当土壤水势高于根系水势时，水分通过渗透作用进入根系。算法通过建立描述水势变化的方程，如 Richards 方程（常用于描述非饱和土壤水分运动），结合根系分布、根系导水率等参数，模拟根系对水分的吸收过程。

2. 植物体内水分运输机制

植物体内的水分运输主要依赖木质部的导管和管胞。水分运输的动力主要来自蒸腾作用产生的负压，形成从叶片到根系的水势梯度，驱动水分向上运输。算法通常运用流体力学原理来模拟这一过程，例如 Hagen-Poiseuille 方程可用于描述管内黏性流体的层流运动。但由于植物木质部结构复杂，实际应用中需要对该方程进行修正，引入反映木质部导管直径、长度、粗糙度等结构特征的参数，以及考虑水分黏性、表面张力等物理性质，从而准确模拟水分在木质部中的运输速率。此外，植物会根据环境条件（如光照强度、温度、湿度）和自身生理状态（如气孔开闭程度）调节蒸腾作用，算法需整合这些调节机制，以实现对动态环境下水分运输过程的精确模拟。

3. 根系与土壤的相互作用

根系与土壤的相互作用对水分吸收至关重要。算法需要考虑根系的空间分布、生长动态以及根系与土壤颗粒的接触情况。根系在土壤中的分布并非均匀，不同植物根系的形态和分布深度存在差异，且会随生长发育阶段发生变化。算法通过建立根系生长模型，结合土壤水分分布，模拟根系在不同土壤区域的水分吸收能力。同时，土壤的物理化学性质（如孔隙度、容重、酸碱度）会影响根系的生长和水分吸收，算法需将这些因素纳入考量，以更真实地反映根系 - 土壤系统的水分交换过程。

构建方法

1. 数值模拟方法

数值模拟是构建植物水分吸收与运输算法的常用手段。该方法通过将植物和土壤系统进行空间离散化，将连续的物理场转化为有限个离散节点上的数值，利用有限差分法、有限元法或有限体积法等数值计算方法求解相关方程。例如，在模拟土壤水分运动时，可将土壤划分为多个网格单元，根据 Richards 方程在每个网格单元上建立差分方程，通过迭代计算得到不同时间步长下各网格单元的土壤含水量，进而分析水分在土壤中的运移规律；对于植物体内的水分运输，可将木质部管道离散化，求解修正后的 Hagen-Poiseuille 方程，获取水分在不同部位的流速和压力分布。

2. 机器学习方法

随着大数据和人工智能技术的发展，机器学习方法逐渐应用于植物水分吸收与运输算法的构建。机器学习算法（如神经网络、随机森林、支持向量机等）能够从大量观测数据中挖掘变量之间的复杂非线性关系。通过收集环境因子（如光照、温度、湿度、风速）、土壤参数（如含水量、质地、养分含量）和植物生理指标（如叶片水势、气孔导度、蒸腾速率）等数据作为输入，以植物水分吸收量或运输速率作为输出，对机器学习模型进行训练，使其能够根据输入数据预测植物的水分过程。例如，利用神经网络强大的非线性拟合能力，可建立环境因素与植物水分运输之间的映射关系，为实时监测和预测植物水分状况提供支持。

3. 多模型耦合方法

植物水分吸收与运输过程受到土壤、植物和大气等多个子系统的共同影响，单一模型难以全面反映其复杂的相互作用。多模型耦合方法将土壤水分模型（如 SWAP 模型）、植物生理模型（如 DALEC 模型）与大气模型（如 WRF 模型）相结合，构建更为综合的生态系统模型。通过数据交换和参数传递，实现各子模型之间的协同模拟，从而更全面地反映植物水分过程与生态环境之间的相互关系。例如，土壤水分模型为植物模型提供根系层的土壤含水量信息，植物模型计算出的蒸腾量又作为大气模型的输入参数，影响区域气候模拟，这种多模型耦合的方式能够提高算法对复杂生态系统的模拟精度。

应用场景

1. 农业领域

在农业生产中，植物水分吸收与运输算法可用于制定精准灌溉策略。通过模拟不同灌溉时间、水量和灌溉方式下植物的水分吸收过程，结合作物生长模型，评估作物的需水规律和生长状况，从而确定最佳灌溉方案，减少水资源浪费，提高作物产量和品质。此外，算法还可用于分析不同土壤类型和气候条件下的农田水分动态，为农田水利设施规划和农业水资源管理提供科学依据。

2. 生态保护领域

在生态保护和恢复工作中，植物水分吸收与运输算法有助于评估植被恢复工程对区域水分循环的影响。通过模拟不同植被类型和种植密度下的植物水分过程，分析其对土壤水分、地下水位和地表径流的影响，为合理选择植被物种、优化植被配置提供参考。同时，算法可用于研究生态系统对气候变化（如降水模式改变、气温升高）的响应，预测植被分布和生态系统功能的变化趋势，为生态保护政策制定提供支持。

3. 林业管理领域

在林业领域，植物水分吸收与运输算法可用于分析树木的水分状况，评估森林生态系统的健康程度。通过模拟不同树种在不同生长阶段的水分吸收与运输过程，结合气象数据和土壤条件，预测树木在干旱等逆境条件下的生存能力，为森林火灾预防、病虫害防治和森林经营管理提供决策依据。此外，算法还可用于研究森林砍伐和造林活动对区域水文循环的影响，促进森林资源的可持续利用。

面临挑战

1. 过程复杂性

植物水分吸收与运输过程涉及众多复杂的生理和物理化学机制，如根系与土壤微生物的相互作用、木质部栓塞的形成与修复、植物激素对水分运输的调控等，目前对这些过程的认识仍存在诸多不足，难以在算法中进行准确刻画，导致模型的模拟精度受限。

2. 参数获取困难

算法的准确性依赖于大量精确的参数，包括土壤水力特性参数（如土壤水分特征曲线、饱和导水率）、植物生理参数（如根系导水率、气孔导度 - 水势关系）等。然而，这些参数的获取往往需要复杂的实验测量，且不同植物、不同土壤条件下参数差异较大，难以获取具有普遍适用性的参数值，增加了模型构建和应用的难度。

3. 尺度转换问题

植物水分吸收与运输过程在不同时空尺度上呈现出不同的特征和规律，从微观的细胞水平到宏观的生态系统水平，从短时间的瞬态变化到长时间的季节和年际变化。如何实现算法在不同尺度上的有效整合和转换，确保模型在各个尺度上都能准确模拟植物水分过程，是当前面临的一大挑战。

📚2 运行结果

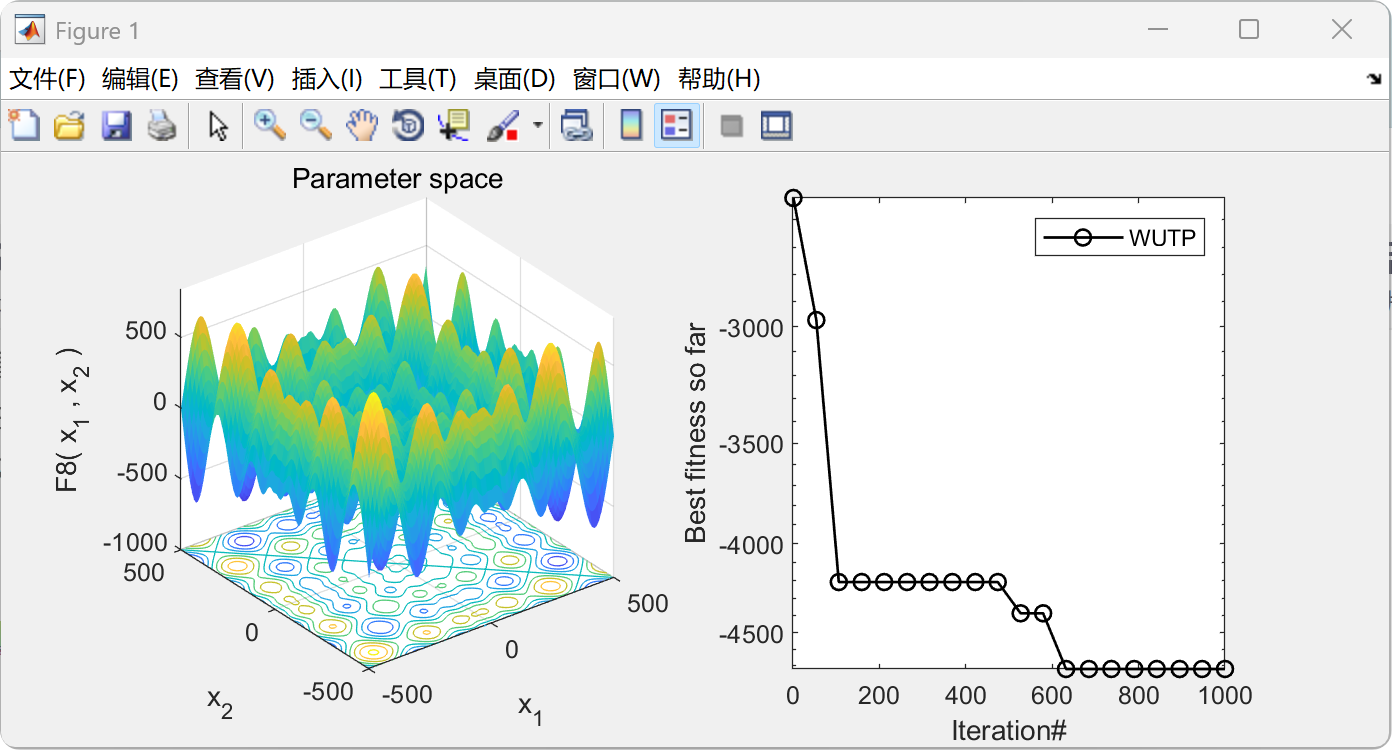
部分代码：

%微信公众号搜索：荧光Matlab，获取更多代码

%%
clc
clear
close all
%%

%%
Fun_name='F8'; % Fun_name of test functions: 'F1' to 'F23'

SearchAgents=30;                      % Fun_name of Pelicans (population members) 
Max_iterations=1000;                  % maximum Fun_name of iteration
[lowerbound,upperbound,dimension,fitness]=fun_info(Fun_name); % Object function information
[Best_score,Best_pos,ESC_curve]=WUTP(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);  % Calculating the solution of the given problem using WUTP 
%%

display(['The best solution obtained by WUTP for ' [num2str(Fun_name)],'  is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by WUTP  for ' [num2str(Fun_name)],'  is : ', num2str(Best_score)]);

figure('Position',[454   445   694   297]);
subplot(1,2,1);
func_plot(Fun_name);     % Function plot
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name,'( x_1 , x_2 )'])
subplot(1,2,2);       % Convergence plot

CNT=20;
k=round(linspace(1,Max_iterations,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:Max_iterations;
if ~strcmp(Fun_name,'F16')&&~strcmp(Fun_name,'F9')&&~strcmp(Fun_name,'F11')  %这里是因为这几个函数收敛太快，不适用于semilogy，直接plot
    semilogy(iter(k),ESC_curve(k),'k-o','linewidth',1);
else
    plot(iter(k),ESC_curve(k),'k-o','linewidth',1);
end