多个机器学习回归器的比较（Matlab）_matlab回归学习器-优快云博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

在机器学习领域，回归分析是解决预测性问题的核心技术之一，旨在建立自变量与因变量之间的定量关系，广泛应用于经济预测、天气预报、医疗诊断等诸多场景。随着技术发展，诞生了多种机器学习回归器，每种回归器都基于独特的算法逻辑和假设前提，适用于不同的数据特征与业务需求。全面了解这些回归器的特性，有助于研究者和从业者根据实际问题选择最优模型，提升预测精度与效率。

线性回归是最基础且应用广泛的回归模型，它基于自变量与因变量之间存在线性关系的假设，通过最小二乘法拟合数据，使预测值与真实值的误差平方和最小化。其优点在于原理简单、可解释性强，模型参数直观反映自变量对因变量的影响程度；但缺点是对非线性数据的拟合能力有限，若数据存在复杂关系，预测误差会显著增大。

决策树回归通过构建树形结构，依据特征的不同取值对数据进行递归划分，直至满足停止条件，每个叶节点对应一个预测值。它对非线性数据具有良好的适应性，能处理数值型和分类型数据，且无需对数据进行复杂的预处理。不过，决策树容易出现过拟合现象，尤其在数据量较小或特征过多时，模型在训练集上表现良好，但在测试集上泛化能力较差。

随机森林回归是基于决策树的集成学习算法，通过构建多个决策树，并将它们的预测结果进行平均，有效降低了单一决策树的过拟合风险，提高了模型的稳定性和泛化能力。它对高维数据和噪声数据具有较好的鲁棒性，在处理大规模数据时表现出色。然而，随机森林的模型复杂度较高，可解释性相比线性回归有所降低，难以直观地分析特征与预测结果之间的关系。

支持向量回归（SVR）基于支持向量机的原理，通过寻找一个最优超平面，使得样本点到该超平面的误差最小化。SVR 在处理小样本、非线性和高维数据时表现优异，能够有效避免过拟合问题。但它对核函数的选择和参数调整较为敏感，不同的核函数和参数设置可能导致模型性能差异较大，需要通过大量的实验来确定最优参数。

梯度提升回归树（GBRT）也是一种集成学习算法，它通过迭代地训练多个弱回归模型（通常为决策树），每次训练都基于前一个模型的残差进行，逐步减少预测误差。GBRT 具有较高的预测精度，能够处理复杂的非线性关系，对异常值和噪声有一定的鲁棒性。但由于其迭代训练的特性，训练时间较长，且模型容易出现过拟合，需要通过适当的正则化方法进行控制。

综上所述，不同的机器学习回归器在原理、性能和适用场景上存在显著差异。线性回归适用于数据呈线性关系且对可解释性要求较高的场景；决策树回归适合初步探索数据特征和处理非线性数据；随机森林回归在处理大规模复杂数据时更具优势；支持向量回归适用于小样本、高维数据的回归问题；梯度提升回归树则在追求高精度预测的同时，需要注意避免过拟合。在实际应用中，应根据数据特点、任务需求和计算资源，综合评估并选择合适的回归器，必要时还可通过模型融合等技术进一步提升预测效果。

📚2 运行结果

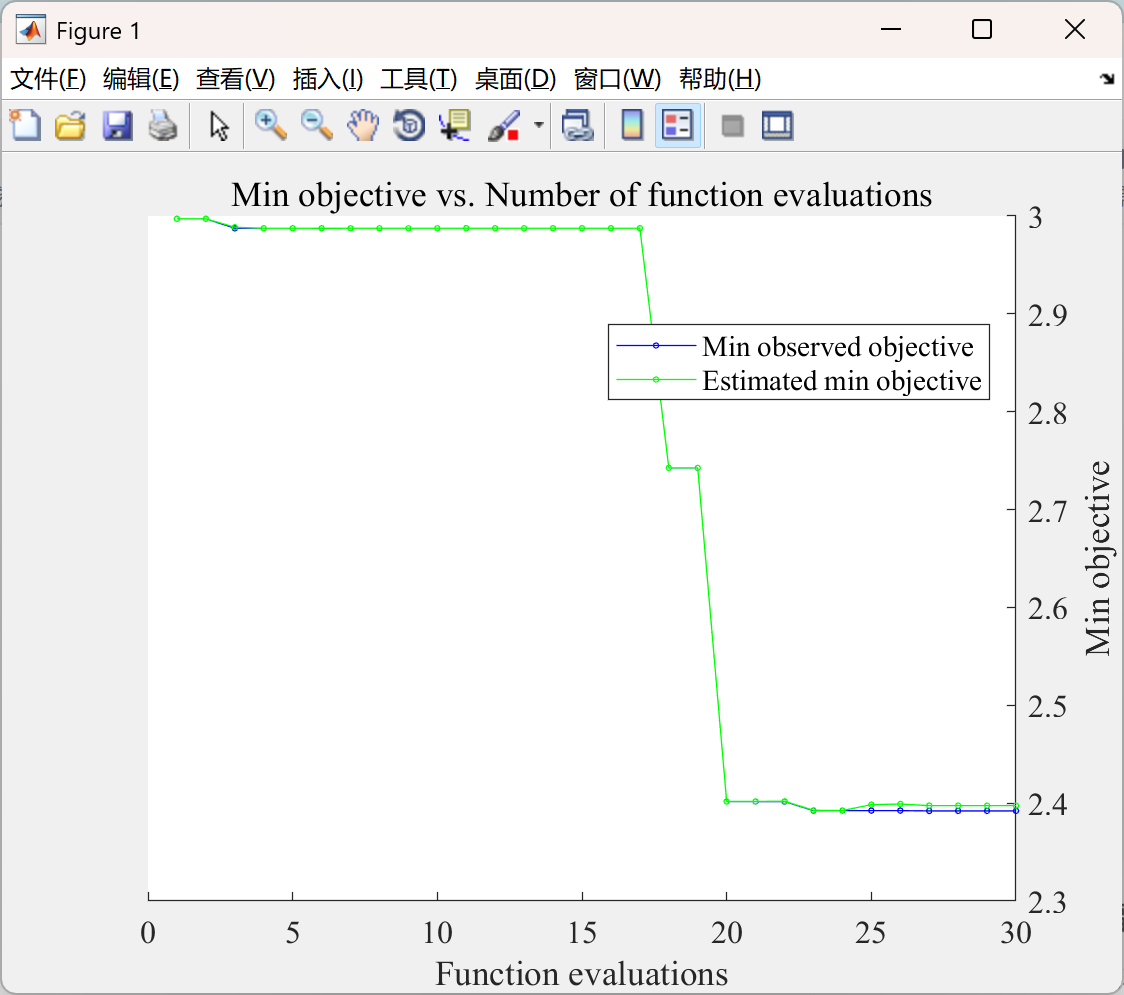
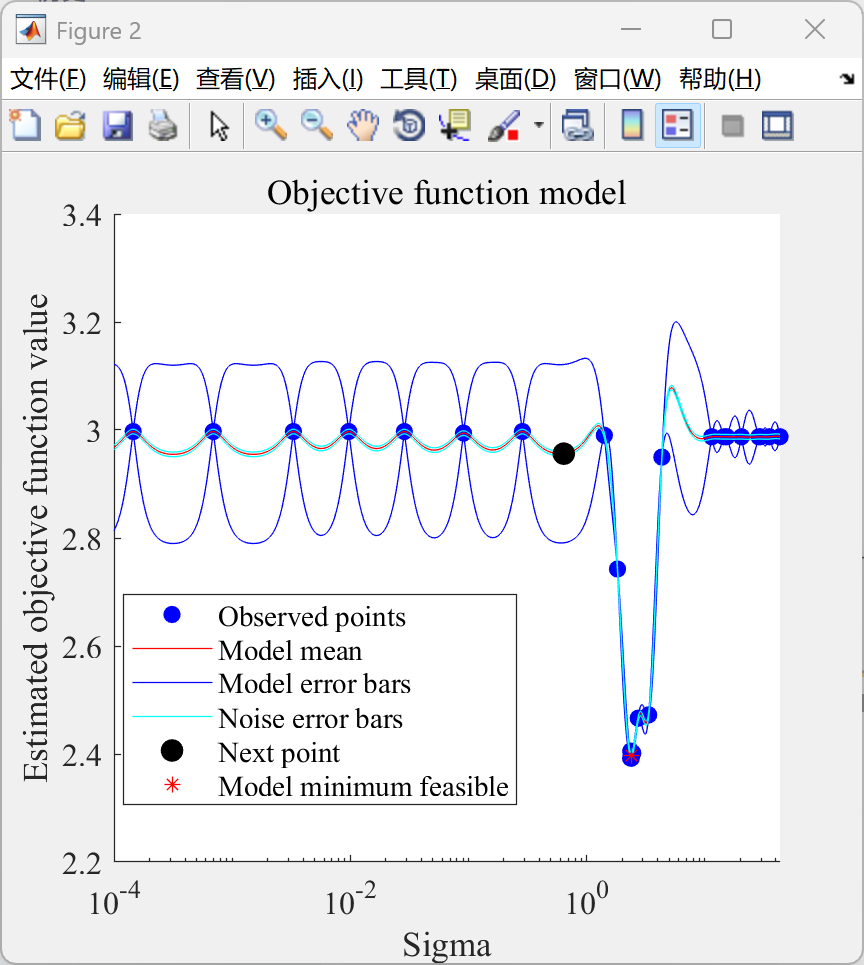
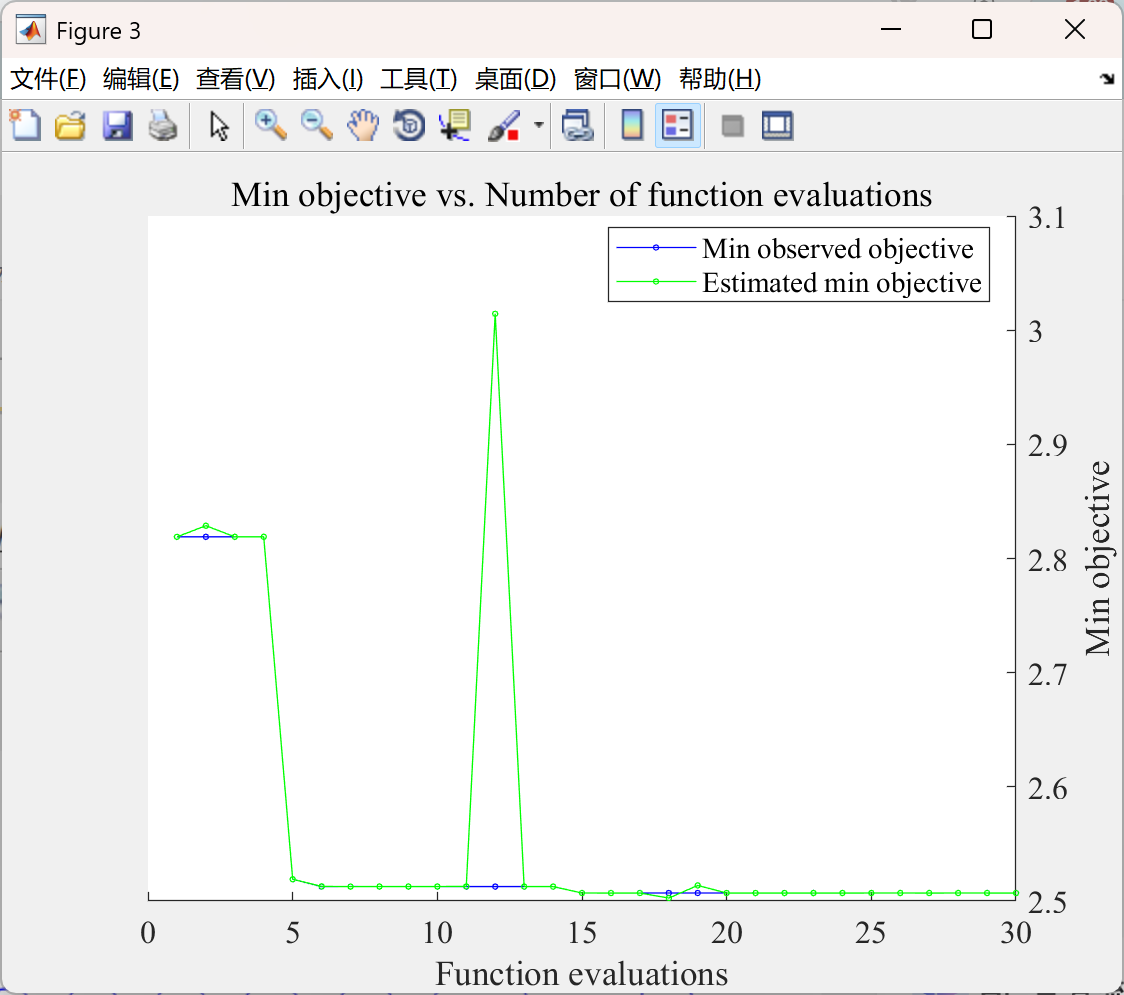
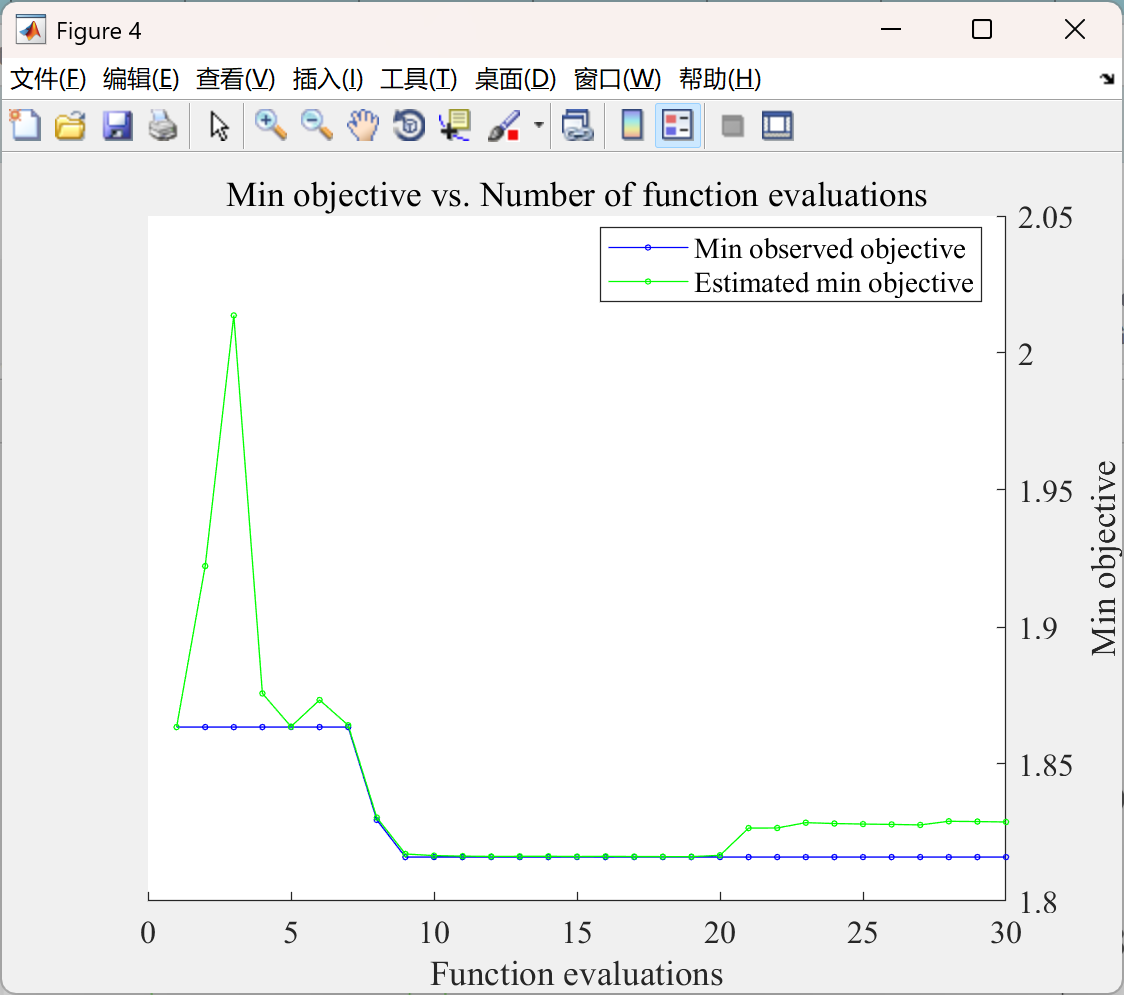
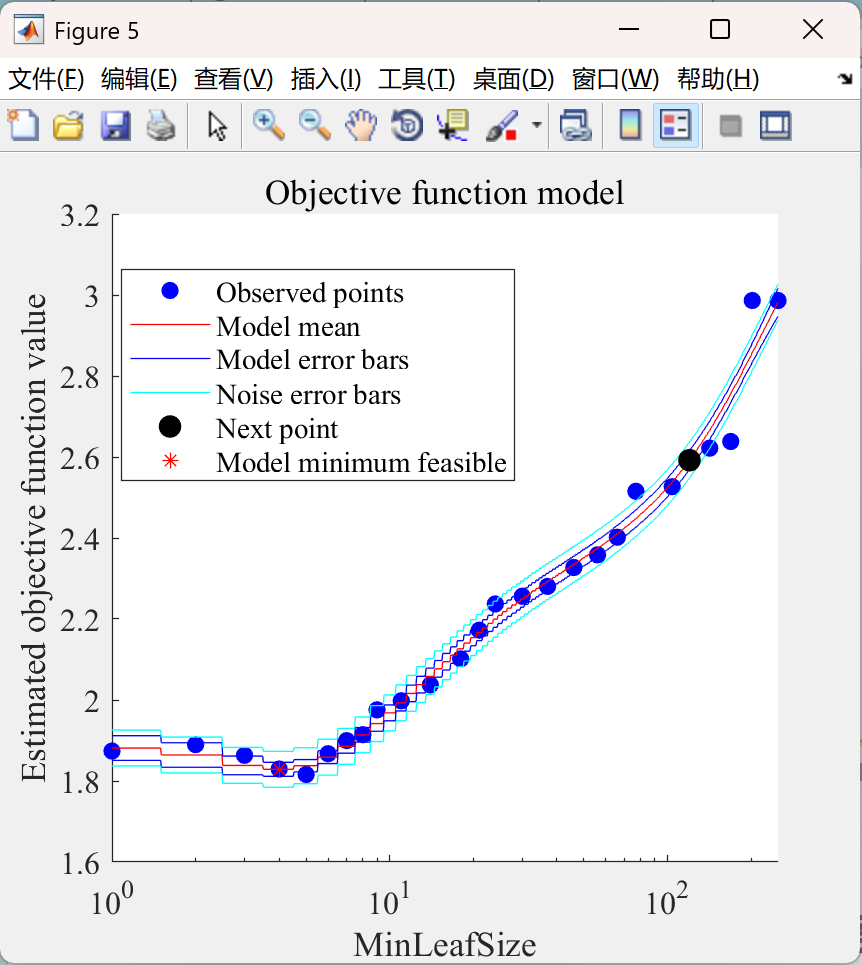
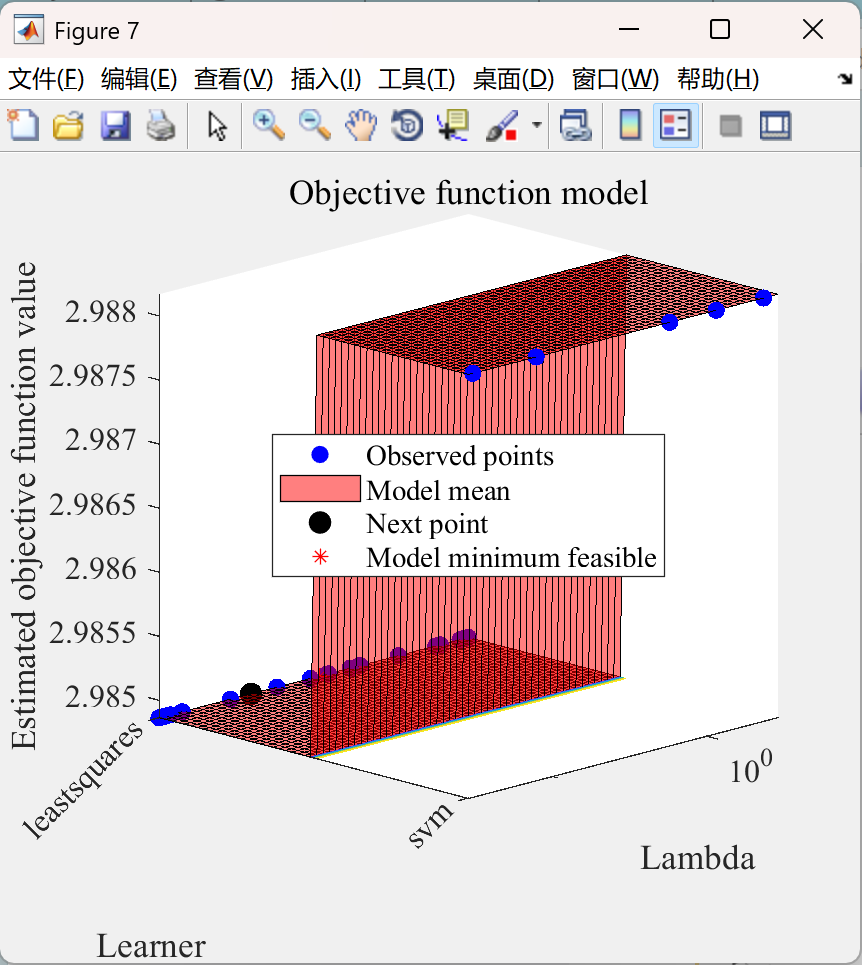
部分代码：

clear all
close all
clc
warning off

set(0,'DefaultAxesFontName', 'Times New Roman')
set(0,'DefaultAxesFontSize', 12)
set(0,'DefaultTextFontname', 'Times New Roman')
set(0,'DefaultTextFontSize', 12)

% Parameters
Runs = 30;  % Number of runs per regressor
kfolds = 5; % Number of cross validation folds

% Dataset
A = load('DS.txt'); % (fi, H [A/m], omega [Hz], a [m]) and  (Tc(掳C), t(s))
X = A(:,1:4);
Y = A(:,5:6);

% Cross-validation folds
kIdx = crossvalind('Kfold', size(X,1), kfolds);

%% SECTION 2 - MODELS SELECTION - Run for each response i
i = 1; % Desired response
    clc
    clear L MM1 MM2 MM3 MM4 MM5 MM6 MM7 RrmseK RrmseKsd M1 M2 M3 M4 M5 M6 M7

    % MODELS HYPERPARAMETER OPTIMIZATION 
    % Regression Gaussian Process
    MM1 = fitrgp(X,Y(:,i),'KernelFunction','squaredexponential',...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',...
    struct('AcquisitionFunctionName','expected-improvement-plus'));
    L(i,1) = MM1.HyperparameterOptimizationResults.MinObjective;

    % Support Vector Machines 
    MM2 = fitrsvm(X,Y(:,i),'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName',...
    'expected-improvement-plus'));
    L(i,2) = MM2.HyperparameterOptimizationResults.MinObjective;

    % Decision Trees
    MM3 = fitrtree(X,Y(:,i),'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName',...
    'expected-improvement-plus'));
    L(i,3) = MM3.HyperparameterOptimizationResults.MinObjective;

    % Linear Regression
    hyperopts = struct('AcquisitionFunctionName','expected-improvement-plus');
    [MM4,FitInfo,HyperparameterOptimizationResults] = fitrlinear(X,Y(:,i),...
    'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',hyperopts);
    L(i,4) = HyperparameterOptimizationResults.MinObjective;

    % Ensemble of learners
    t = templateTree('Reproducible',true);
    MM5 = fitrensemble(X,Y(:,i),'OptimizeHyperparameters','auto','Learners',t, ...
    'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus'));
    L(i,5) = MM5.HyperparameterOptimizationResults.MinObjective;

    % Kernels
    [MM6,FitInfo,HyperparameterOptimizationResults] = fitrkernel(X,Y(:,i),'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus'));
    L(i,6) = HyperparameterOptimizationResults.MinObjective;

    % Artificial Neural Networks   
    MM7 = fitrnet(X,Y(:,i),"OptimizeHyperparameters","auto", ...
    "HyperparameterOptimizationOptions",struct("AcquisitionFunctionName","expected-improvement-plus"));
    L(i,7) = MM7.HyperparameterOptimizationResults.MinObjective;

     
    % MODELS COMPARISON THROUGH CROSS VALIDATION
    for k = 1 : kfolds
    % Splitting into trainning and test data
    % Trainning
    Predictors = X(kIdx~=k,:);
    Response = Y(kIdx~=k,i);
    % Testing
    TEX = X(kIdx==k,:);
    TEY = Y(kIdx==k,i);
    % Normalizing
        % extracting normalization factors from training data
         minimums = min(Predictors, [], 1);
         ranges = max(Predictors, [], 1) - minimums;
        % normalizing training data	
         Predictors = (Predictors - repmat(minimums, size(Predictors, 1), 1)) ./ repmat(ranges, size(Predictors, 1), 1);
        % normalizing testing data based on factors extracted from training data
         TEX = (TEX - repmat(minimums, size(TEX, 1), 1)) ./ repmat(ranges, size(TEX, 1), 1);

    for j = 1 : Runs
    % RGP 
    M1 = fitrgp(...
    Predictors, ...
    Response, ...
    'BasisFunction', MM1.BasisFunction, ...
    'KernelFunction', MM1.KernelFunction, ...
    'Sigma', MM1.Sigma, ...
    'Standardize', false);
    RMSEteste(j,1) = rmse(TEY,predict(M1,TEX));

    % SVM
    responseScale = iqr(Response);
    if ~isfinite(responseScale) || responseScale == 0.0
    responseScale = 1.0;
    end
    boxConstraint = responseScale/1.349;
    epsilon = responseScale/13.49;
    M2 = fitrsvm(...
        Predictors, ...
        Response, ...
        'KernelFunction', 'gaussian', ...
        'PolynomialOrder', [], ...
        'KernelScale', MM2.KernelParameters.Scale, ...
        'BoxConstraint', boxConstraint, ...
        'Epsilon', epsilon, ...
        'Standardize', false);
    RMSEteste(j,2) = rmse(TEY,predict(M2,TEX));

    % DT
    M3 = fitrtree(...
    Predictors, ...
    Response, ...
    'MinLeafSize', MM3.HyperparameterOptimizationResults.XAtMinObjective.MinLeafSize, ...
    'Surrogate', 'off');
    RMSEteste(j,3) = rmse(TEY,predict(M3,TEX));

    % LR 
    M4 = fitrlinear(Predictors,Response,'Lambda',MM4.Lambda,...
    'Learner',MM4.Learner,'Solver','sparsa','Regularization','lasso');
    RMSEteste(j,4) = rmse(TEY,predict(M4,TEX));

    % ENS
    template = templateTree(...
    'MinLeafSize', MM5.HyperparameterOptimizationResults.XAtMinObjective.MinLeafSize, ...
    'NumVariablesToSample', 'all');
    Method = char(MM5.HyperparameterOptimizationResults.XAtMinObjective.Method);
    M5 = fitrensemble(...
    Predictors, ...
    Response, ...
    'Method', Method, ...
    'NumLearningCycles', MM5.HyperparameterOptimizationResults.XAtMinObjective.NumLearningCycles, ...
    'Learners', template);
    RMSEteste(j,5) = rmse(TEY,predict(M5,TEX));

    % KERNELS
    M6 = fitrkernel(...
    Predictors, ...
    Response, ...
    'Learner', MM6.Learner, ...
    'NumExpansionDimensions', MM6.NumExpansionDimensions, ...
    'Lambda', MM6.Lambda, ...
    'KernelScale', MM6.KernelScale, ...
    'IterationLimit', 1000);
    RMSEteste(j,6) = rmse(TEY,predict(M6,TEX));

    % ANN
    M7 = fitrnet(...
    Predictors, ...
    Response, ...
    'LayerSizes', MM7.LayerSizes, ...
    'Activations', MM7.Activations, ...
    'Lambda', MM7.HyperparameterOptimizationResults.XAtMinObjective.Lambda, ...
    'IterationLimit', 1000, ...
    'Standardize', false);
    RMSEteste(j,7) = rmse(TEY,predict(M7,TEX));
    end
    RrmseK(k,:) = mean(RMSEteste);
    RrmseKsd(k,:) = std(RMSEteste);
    end
Rrmse = mean(RrmseK);
Rrmsesd = mean(RrmseKsd);
[a,b]=min(Rrmse);
% SELECTION RESULTS
disp('Best Model')
if b == 1; disp('RGP'); end
if b == 2; disp('SVM'); end
if b == 3; disp('DT'); end
if b == 4; disp('LR'); end
if b == 5; disp('ENSEMBLE'); end
if b == 6; disp('KERNEL'); end
if b == 7; disp('ANN'); end
disp('Loss in the BO')