【信号处理】实现主成分分析 (PCA)（Matlab实现）

荧光Matlab

已于 2025-04-23 10:51:57 修改

阅读量1k

点赞数 7

CC 4.0 BY-SA版权

文章标签：信息可视化数据分析数据挖掘

于 2025-04-22 15:11:52 首次发布

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/147395060

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

实现主成分分析 (PCA) 概述

一、引言

在大数据时代，数据规模不断膨胀，高维数据带来的 “维数灾难” 问题日益突出。高维数据不仅增加计算复杂度，还可能引入冗余信息，干扰数据分析与模型构建。主成分分析（Principal Component Analysis，PCA）作为一种高效的数据降维技术，能够在保留数据主要信息的前提下，将高维数据映射到低维空间，简化数据结构，提升数据分析效率与模型性能，在机器学习、计算机视觉、生物信息学等众多领域发挥着关键作用。

二、PCA 核心原理

数据相关性与方差表征

PCA 的核心思想基于数据的相关性和方差。在高维数据中，各维度特征之间往往存在一定相关性，部分维度可能携带相似或冗余信息。方差用于衡量数据在某一维度上的离散程度，方差越大，意味着该维度数据蕴含的信息越丰富。PCA 旨在寻找一组新的正交基（主成分），使得数据在这些新基上的投影方差尽可能大，从而将数据映射到少数几个方差较大的主成分方向上，实现数据降维的同时保留关键信息。

协方差矩阵与特征分解

为了找到这些主成分，需要对数据的协方差矩阵进行分析。协方差矩阵描述了数据不同维度之间的线性相关关系，通过对协方差矩阵进行特征分解，可以得到其特征值和特征向量。特征值大小对应主成分的重要程度，特征值越大，表明该主成分方向上数据的方差越大，蕴含信息越多；特征向量则确定了主成分的方向。将数据投影到由特征向量构成的新坐标系中，就实现了数据从原始高维空间到低维主成分空间的转换。

三、应用场景

数据可视化

在高维数据可视化中，PCA 能将数据降至二维或三维空间，方便在平面或三维坐标系中直观展示数据分布、聚类结构和样本间关系。例如，在图像数据集可视化中，通过 PCA 将高维图像特征映射到低维空间，可清晰呈现不同图像类别之间的界限和相似性。

机器学习预处理

在机器学习任务中，PCA 常用于数据预处理。降维后的低维数据可减少模型训练时间，降低计算成本，同时避免过拟合问题。在图像识别中，对图像像素特征进行 PCA 降维后，再输入分类模型，可提高模型训练速度和分类准确率。

信号处理

在信号处理领域，PCA 可用于去除信号中的噪声和冗余成分，提取信号的主要特征。例如，在语音信号处理中，对语音特征进行 PCA 降维，能有效提取语音的关键特征，提高语音识别系统的性能。

四、优势与局限

优势

高效降维：PCA 能够在保留数据主要信息的基础上，大幅降低数据维度，简化数据结构，提高数据处理效率和模型训练速度。

无监督学习：作为无监督学习方法，PCA 无需数据的标签信息，仅依据数据自身的分布特征进行降维，适用范围广泛。

正交变换：PCA 得到的主成分相互正交，消除了原始数据特征之间的相关性，便于后续数据分析和模型构建。

局限

线性假设：PCA 基于线性变换，仅适用于数据具有线性结构的情况，对于非线性数据，降维效果可能不佳。

缺乏可解释性：主成分是原始特征的线性组合，其物理意义往往不直观，难以直接解释每个主成分代表的实际含义。

信息损失：尽管 PCA 能保留大部分信息，但降维过程不可避免会丢失部分信息，若选取的主成分数量过少，可能影响数据分析结果的准确性。

五、改进与拓展

核主成分分析（KPCA）

针对 PCA 的线性局限，核主成分分析（Kernel PCA，KPCA）引入核函数，将原始数据映射到高维特征空间，在高维空间中进行主成分分析，从而实现非线性数据的降维。KPCA 通过核技巧避免了在高维空间中直接计算，降低计算复杂度，在处理非线性数据时具有更好的效果。

增量式主成分分析（IPCA）

传统 PCA 需要一次性处理全部数据，当数据量过大时，内存消耗大且计算效率低。增量式主成分分析（Incremental PCA，IPCA）能够逐步处理数据，在新数据不断到来时，无需重新计算整个数据集的协方差矩阵，可动态更新主成分，适用于大数据流环境下的数据降维。

主成分分析作为经典的数据降维技术，以其简洁高效的特点在众多领域广泛应用。尽管存在一定局限性，但通过不断改进和拓展，PCA 在数据处理和分析中持续发挥重要作用，为解决高维数据问题提供了有力工具。

📚2 运行结果

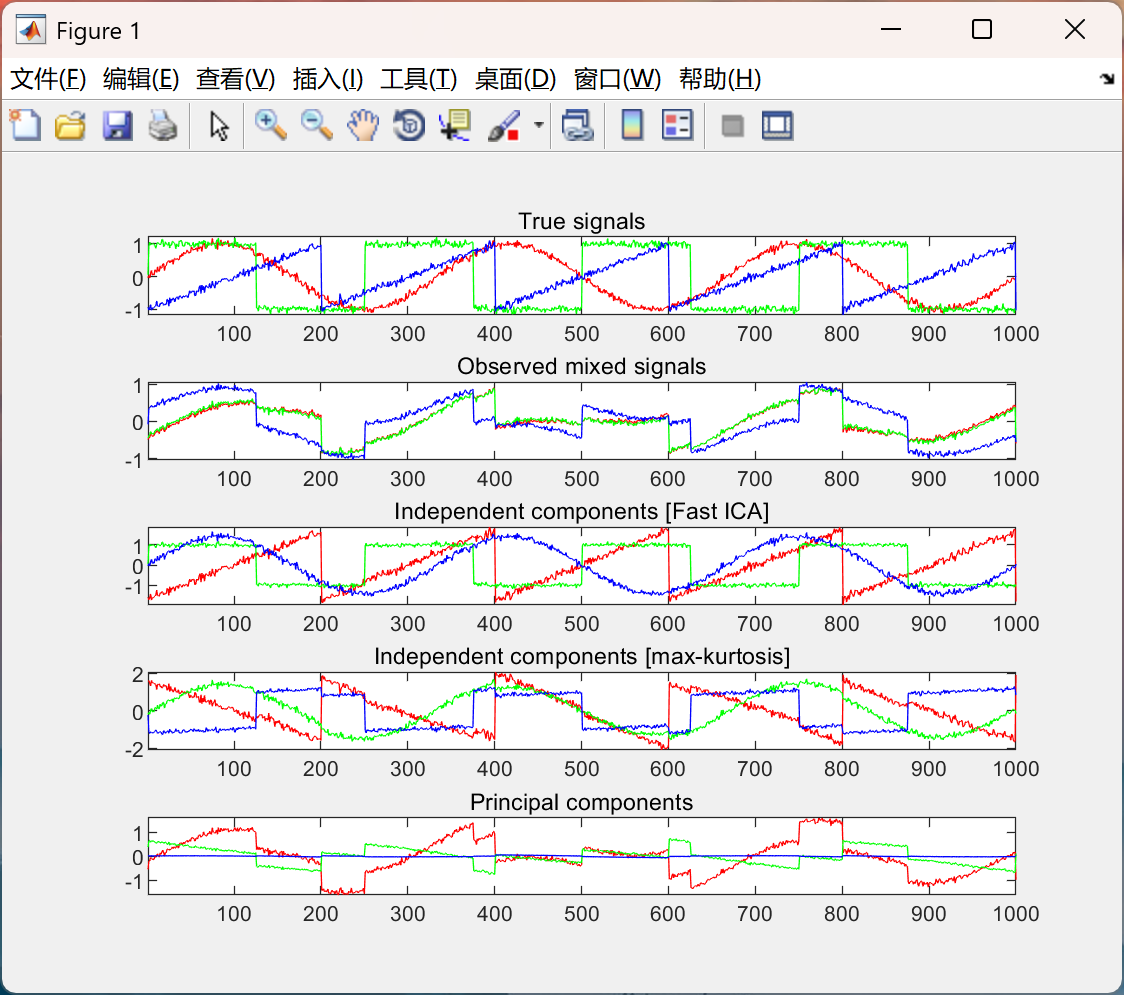
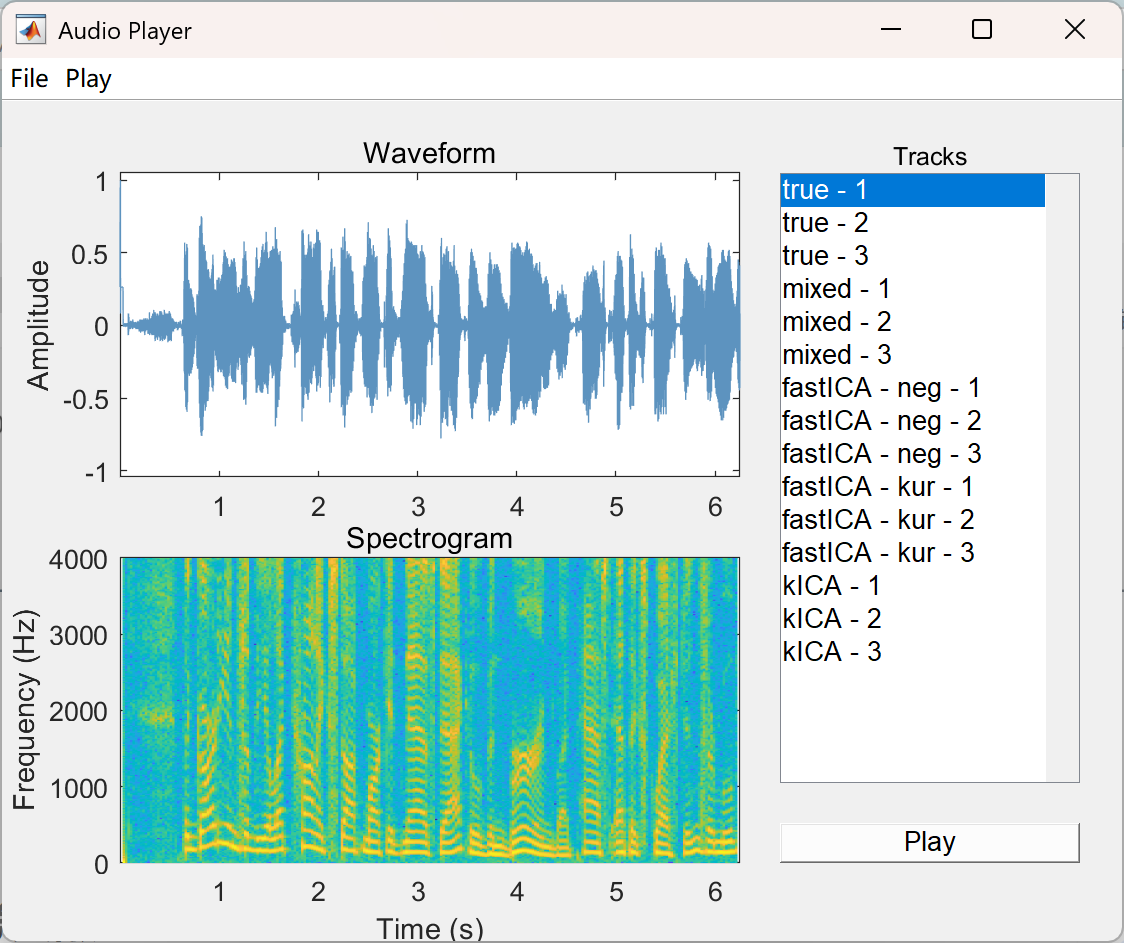
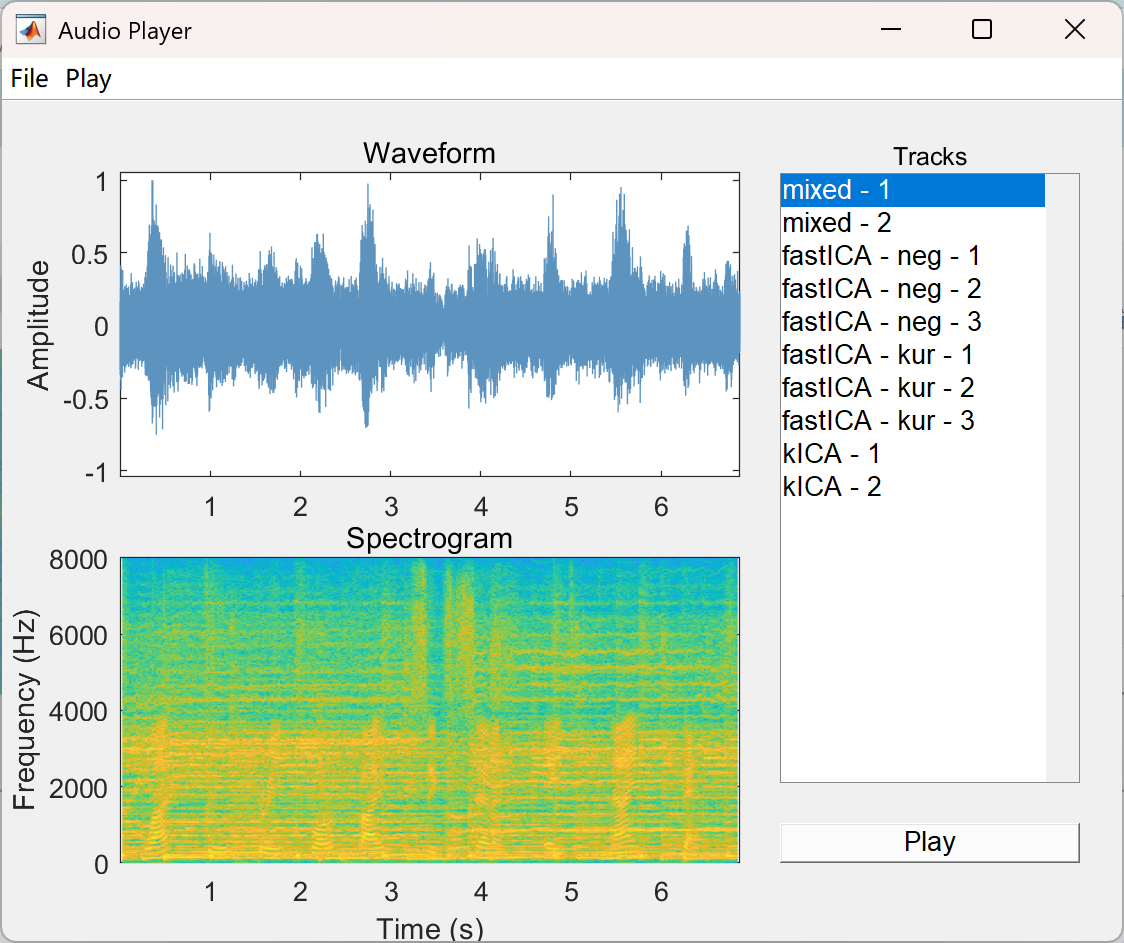
部分代码：


%% ICA demo (signals)

rng(42);

% Knobs
n   = 1000;             % # samples
T   = [3, 4, 5];        % # periods for each signal
SNR = 50;               % Signal SNR
d   = 3;                % # mixed observations
r   = 3;                % # independent/principal components

% Generate ground truth
t = @(n,T) linspace(0,1,n) * 2 * pi * T;
Ztrue(1,:) = sin(t(n,T(1)));            % Sinusoid
Ztrue(2,:) = sign(sin(t(n,T(2))));      % Square
Ztrue(3,:) = sawtooth(t(n,T(3)));       % Sawtooth

% Add some noise to make the signals "look" interesting
sigma = @(SNR,X) exp(-SNR / 20) * (norm(X(:)) / sqrt(numel(X)));
Ztrue = Ztrue + sigma(SNR,Ztrue) * randn(size(Ztrue));

% Generate mixed signals
normRows = @(X) bsxfun(@rdivide,X,sum(X,2));
A = normRows(rand(d,3));
Zmixed = A * Ztrue;

% Perform Fast ICA
Zfica = fastICA(Zmixed,r);

% Perform max-kurtosis ICA
Zkica = kICA(Zmixed,r);

% Perform PCA
Zpca = PCA(Zmixed,r);

%--------------------------------------------------------------------------
% Plot results
%--------------------------------------------------------------------------
cm = hsv(max([3, r, d]));
%cm = linspecer(max([3, r, d]));

figure();

% Truth
subplot(5,1,1);
for i = 1:3
    plot(Ztrue(i,:),'-','Color',cm(i,:)); hold on;
end
title('True signals');
axis tight;

% Observations
subplot(5,1,2);
for i = 1:d
    plot(Zmixed(i,:),'-','Color',cm(i,:)); hold on;
end
title('Observed mixed signals');
axis tight;

% Fast ICA
subplot(5,1,3);
for i = 1:r
    plot(Zfica(i,:),'-','Color',cm(i,:)); hold on;
end
title('Independent components [Fast ICA]');
axis tight;

% Max-kurtosis
subplot(5,1,4);
for i = 1:r
    plot(Zkica(i,:),'-','Color',cm(i,:)); hold on;
end
title('Independent components [max-kurtosis]');
axis tight;

% PCA
subplot(5,1,5);
for i = 1:r
    plot(Zpca(i,:),'-','Color',cm(i,:)); hold on;
end
title('Principal components');
axis tight;
%--------------------------------------------------------------------------

%% ICA demo (audio)
%
% Audio descriptions
%
% source1: siren
% source2: news (stocks)
% source3: foreign 1
% source4: news (food)
% source5: music (classical)
% source6: foreign 2
% source7: music (opera)
% source7: foreign 3
% source9: music (pop)
%
% voice1: talking (linear algebra)
% voice2: talking (sports)
%

rng(42);

% Knobs
Fs = 8000; % Sampling rate of input audio
paths = {'audio/source2.wav','audio/source3.wav','audio/source5.wav'};
%paths = {'audio/voice1.mat','audio/voice2.mat'};
[p, d, r] = deal(numel(paths));
A = randomMixingMatrix(d,p);
%A = [0.6, 0.4; 0.4, 0.6];

% Load audio
Ztrue = loadAudio(paths);

% Generate mixed signals
Zmixed = normalizeAudio(A * Ztrue);

% Fast ICA (negentropy)
Zica1 = normalizeAudio(fastICA(Zmixed,r,'negentropy'));

% Fast ICA (kurtosis)
Zica2 = normalizeAudio(fastICA(Zmixed,r,'kurtosis'));

% Max-kurtosis ICA
Zica3 = normalizeAudio(kICA(Zmixed,r));

%--------------------------------------------------------------------------
% Plot results
%--------------------------------------------------------------------------
audio = [];

% True waveforms
for i = 1:p
    audio(end + 1).y = Ztrue(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('true - %d',i);
end

% Mixed waveforms
for i = 1:d
    audio(end + 1).y = Zmixed(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('mixed - %d',i);
end

% Fast ICA (negentropy) waveforms
for i = 1:r
    audio(end + 1).y = Zica1(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('fastICA - neg - %d',i);
end

% Fast ICA (kurtosis) waveforms
for i = 1:r
    audio(end + 1).y = Zica2(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('fastICA - kur - %d',i);
end

% Max-kurtosis ICA waveforms
for i = 1:r
    audio(end + 1).y = Zica3(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('kICA - %d',i);
end

% Play audio
PlayAudio(audio);
%--------------------------------------------------------------------------

%% ICA demo (pre-mixed audio)
% TODO(brimoor): how to get this to work?
%
% Audio descriptions
%
% rsm2_mA/B: music + counting english
%  rss_mA/B: counting english + counting spanish
%  rssd_A/B: talking english + talking spanish
%

rng(42);

% Knobs
Fs    = 16000; % Sampling rate of input audio
paths = {'audio/rsm2_mA.wav','audio/rsm2_mB.wav'};
%paths = {'audio/rss_mA.wav','audio/rss_mB.wav'};
%paths = {'audio/rssd_A.wav','audio/rssd_B.wav'};
[d, r] = deal(numel(paths));
r = r + 1;

% Load audio
Zmixed = loadAudio(paths);

% Fast ICA (negentropy)
Zica1 = normalizeAudio(fastICA(Zmixed,r,'negentropy'));

% Fast ICA (kurtosis)
Zica2 = normalizeAudio(fastICA(Zmixed,r,'kurtosis'));

% Max-kurtosis ICA
Zica3 = normalizeAudio(kICA(Zmixed,min(r,d)));

%--------------------------------------------------------------------------
% Plot results
%--------------------------------------------------------------------------
audio = [];

% Mixed waveforms
for i = 1:d
    audio(end + 1).y = Zmixed(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('mixed - %d',i);
end

% Fast ICA (negentropy) waveforms
for i = 1:r
    audio(end + 1).y = Zica1(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('fastICA - neg - %d',i);
end

% Fast ICA (kurtosis) waveforms
for i = 1:r
    audio(end + 1).y = Zica2(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('fastICA - kur - %d',i);
end

% Max-kurtosis ICA waveforms
for i = 1:min(r,d)
    audio(end + 1).y = Zica3(i,:); %#ok
    audio(end).Fs    = Fs;
    audio(end).name  = sprintf('kICA - %d',i);
end