【图像加密】基于分数阶傅里叶变换和曲线锯变换的图像加密（Matlab实现）

荧光Matlab

已于 2025-04-18 19:49:10 修改

阅读量883

点赞数 13

CC 4.0 BY-SA版权

文章标签： matlab 开发语言

于 2025-04-18 19:44:19 首次发布

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/147339316

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、引言

在信息爆炸的时代，图像作为一种直观且信息丰富的载体，广泛应用于医疗诊断、军事侦察、电子商务、数字媒体等多个领域。随着互联网技术的飞速发展，图像在传输和存储过程中面临着信息泄露、恶意篡改等安全威胁，因此，图像加密技术成为保障信息安全的关键手段。分数阶傅里叶变换和曲线锯变换作为两种独特的数学工具，各自具有良好的特性，将它们有机结合应用于图像加密，为图像信息安全提供了新的解决思路和技术途径，受到了学术界和工程界的广泛关注。

二、分数阶傅里叶变换与曲线锯变换原理

分数阶傅里叶变换原理

分数阶傅里叶变换（Fractional Fourier Transform，FRFT）是传统傅里叶变换的推广和延伸，它将信号从时间域到频率域的映射扩展到了一个介于时间和频率之间的分数阶域。在分数阶傅里叶变换中，信号可以在不同的分数阶次下进行变换，不同的分数阶次对应着不同的变换角度，通过改变分数阶次，可以实现对信号在时间 - 频率平面上的多角度分析。从数学角度来看，分数阶傅里叶变换可以通过积分变换的形式来定义，其变换核函数与分数阶次密切相关。这种变换特性使得分数阶傅里叶变换在处理具有时频局部特性的信号时具有独特的优势，能够更灵活地对信号进行处理和分析。

曲线锯变换原理

曲线锯变换（Curvelet Transform）是一种多尺度几何分析工具，它能够有效地捕捉图像中的曲线和边缘等几何结构信息。曲线锯变换基于多尺度分析和方向分析，将图像分解为不同尺度、不同方向的子带。在多尺度分解过程中，图像被逐步分解为低频近似部分和高频细节部分，低频部分保留了图像的主要结构信息，高频部分则包含了图像的边缘、纹理等细节信息。在方向分析阶段，曲线锯变换通过构造一系列具有不同方向的基函数，对高频细节部分进行方向分解，使得曲线锯变换能够在多个方向上对图像的曲线结构进行精确表示。这种特性使得曲线锯变换在处理具有复杂几何结构的图像时，相比传统的小波变换等方法，能够更稀疏地表示图像，从而更有效地提取图像的重要特征。

三、基于两种变换的图像加密流程

图像预处理

在进行图像加密之前，首先需要对原始图像进行预处理。预处理步骤通常包括图像灰度化（如果原始图像为彩色图像），将彩色图像转换为灰度图像，以简化后续的加密处理；图像归一化，将图像的像素值映射到一个特定的范围内，如 [0, 1]，使得图像数据具有统一的尺度，便于进行数学运算；此外，还可能包括图像去噪等操作，去除图像在采集和传输过程中引入的噪声，提高加密的质量和安全性。

分数阶傅里叶变换加密

对预处理后的图像进行分数阶傅里叶变换。选择合适的分数阶次，将图像从空间域变换到分数阶域。在分数阶域中，图像的像素值分布和结构信息发生了改变，原始图像的特征被隐藏。通过选择不同的分数阶次，可以实现对图像的不同加密效果，分数阶次成为加密过程中的一个重要密钥。在分数阶域中，对变换后的图像进行进一步的处理，如对像素值进行扰乱、置换等操作，进一步增加图像的混乱程度，使得加密后的图像难以被破译。

曲线锯变换加密

在完成分数阶傅里叶变换加密后，对图像进行曲线锯变换。将图像分解为不同尺度和方向的曲线锯系数，这些系数包含了图像在不同尺度和方向上的结构信息。利用密钥对曲线锯系数进行量化、编码等操作，改变系数的取值，进一步打乱图像的结构信息，增强加密的安全性。同时，可以对曲线锯系数进行选择性保留或丢弃，以实现对图像信息的进一步隐藏。

后处理与密钥生成

对经过分数阶傅里叶变换和曲线锯变换加密后的图像进行后处理，如对图像进行归一化、缩放等操作，使其满足特定的存储和传输要求。在加密过程中，分数阶傅里叶变换的分数阶次、曲线锯变换的参数设置以及对系数的处理方式等都构成了加密的密钥。将这些密钥进行妥善保存和管理，在解密过程中需要使用这些密钥来恢复原始图像。

四、优势分析

高安全性

结合分数阶傅里叶变换和曲线锯变换的图像加密方法，利用了两种变换在不同域对图像进行处理的特性，大大增加了加密的复杂度。分数阶傅里叶变换的分数阶次和曲线锯变换的参数等密钥空间较大，使得攻击者难以通过穷举法破解密钥。同时，两种变换对图像的像素值和结构信息进行了双重扰乱和隐藏，加密后的图像与原始图像在视觉上和信息结构上都有很大差异，提高了加密图像的安全性，能够有效抵御多种攻击，如统计分析攻击、差分攻击等。

良好的图像特征保留与重建

分数阶傅里叶变换和曲线锯变换都具有良好的数学性质，能够在加密过程中较好地保留图像的重要特征。在解密过程中，通过正确使用密钥，能够准确地从加密图像中重建原始图像，恢复图像的细节和结构信息，保证了图像加密和解密的可逆性，使得加密后的图像在传输和存储后能够被正确还原，满足实际应用的需求。

适应性强

该加密方法对不同类型的图像，如自然图像、医学图像、遥感图像等都具有较好的适应性。无论是图像的内容复杂程度如何，都能够通过调整分数阶傅里叶变换和曲线锯变换的参数，实现有效的加密。同时，该方法可以根据不同的应用场景和安全需求，灵活地调整加密的强度和方式，具有较强的实用性。

五、面临的挑战与发展方向

计算复杂度高

分数阶傅里叶变换和曲线锯变换本身都涉及到较为复杂的数学运算，尤其是曲线锯变换在多尺度和方向分解过程中计算量较大。将两种变换结合用于图像加密，进一步增加了计算复杂度，导致加密和解密的时间较长，难以满足实时性要求较高的应用场景，如实时视频流加密等。因此，如何降低算法的计算复杂度，提高加密和解密的效率，是该技术面临的一个重要挑战。

密钥管理难度大

由于加密过程涉及到多个密钥，如分数阶傅里叶变换的分数阶次、曲线锯变换的参数等，密钥的生成、存储和传输都需要进行严格的管理。如果密钥泄露，将导致加密图像被破解，造成信息泄露。因此，需要研究更加安全、有效的密钥管理方案，如采用密钥分发中心、密钥加密技术等，确保密钥的安全性和可靠性。

发展方向

未来，基于分数阶傅里叶变换和曲线锯变换的图像加密技术可以朝着以下方向发展：一是结合其他先进的加密技术，如混沌理论、量子加密等，进一步提高加密的安全性和性能；二是研究快速算法和并行计算技术，降低算法的计算复杂度，提高加密和解密的效率，以适应实时性要求较高的应用场景；三是加强对密钥管理技术的研究，探索更加安全、便捷的密钥生成、存储和传输方式；四是拓展该技术在更多领域的应用，如物联网、区块链等，为信息安全提供更全面的保障。

六、结论

基于分数阶傅里叶变换和曲线锯变换的图像加密技术，充分发挥了两种变换的优势，为图像信息安全提供了一种有效的解决方案。该技术具有高安全性、良好的图像特征保留与重建能力以及较强的适应性等优点，但也面临着计算复杂度高、密钥管理难度大等挑战。随着相关研究的不断深入和技术的不断发展，相信该技术将不断完善和优化，在图像信息安全领域发挥更加重要的作用，为保障图像信息的安全传输和存储提供坚实的技术支持。

📚2 运行结果

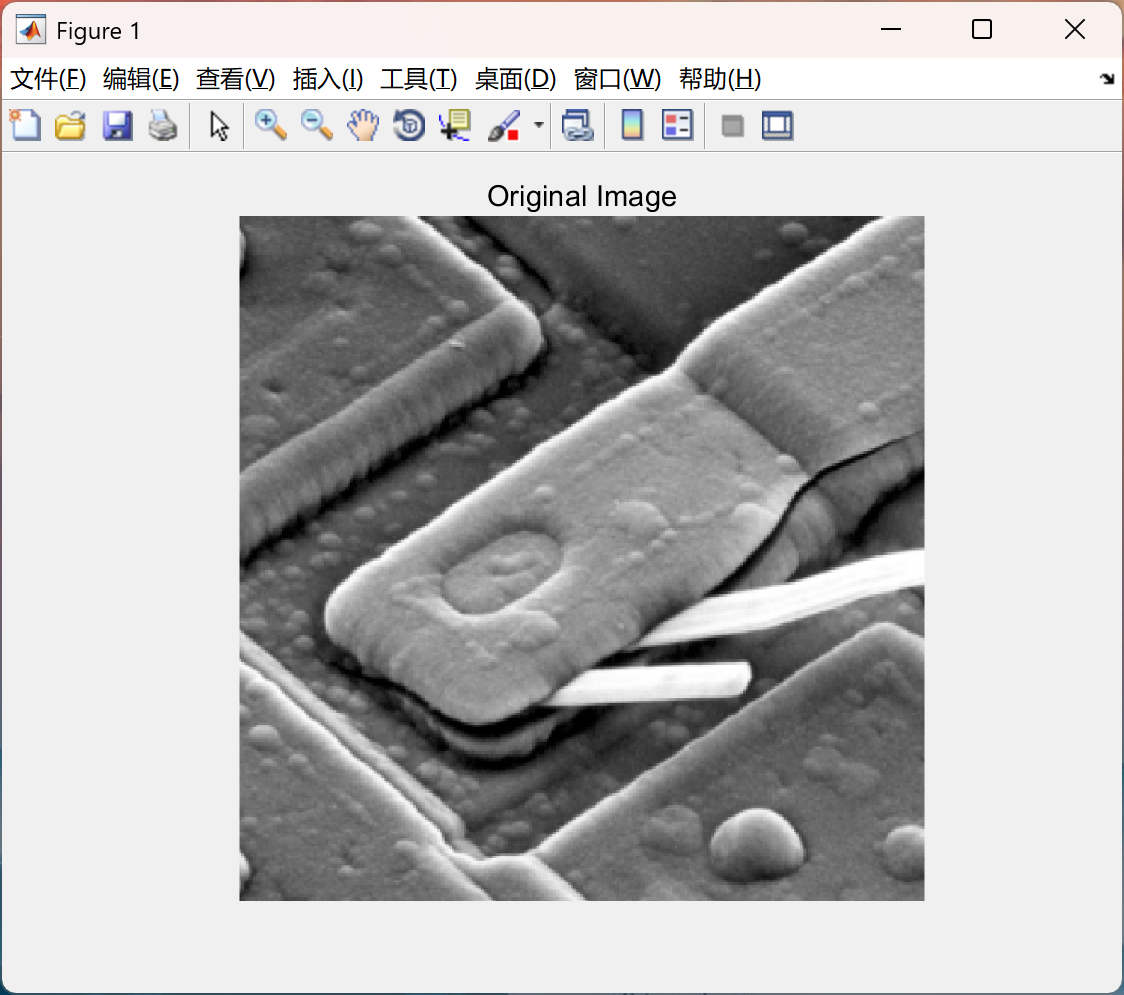
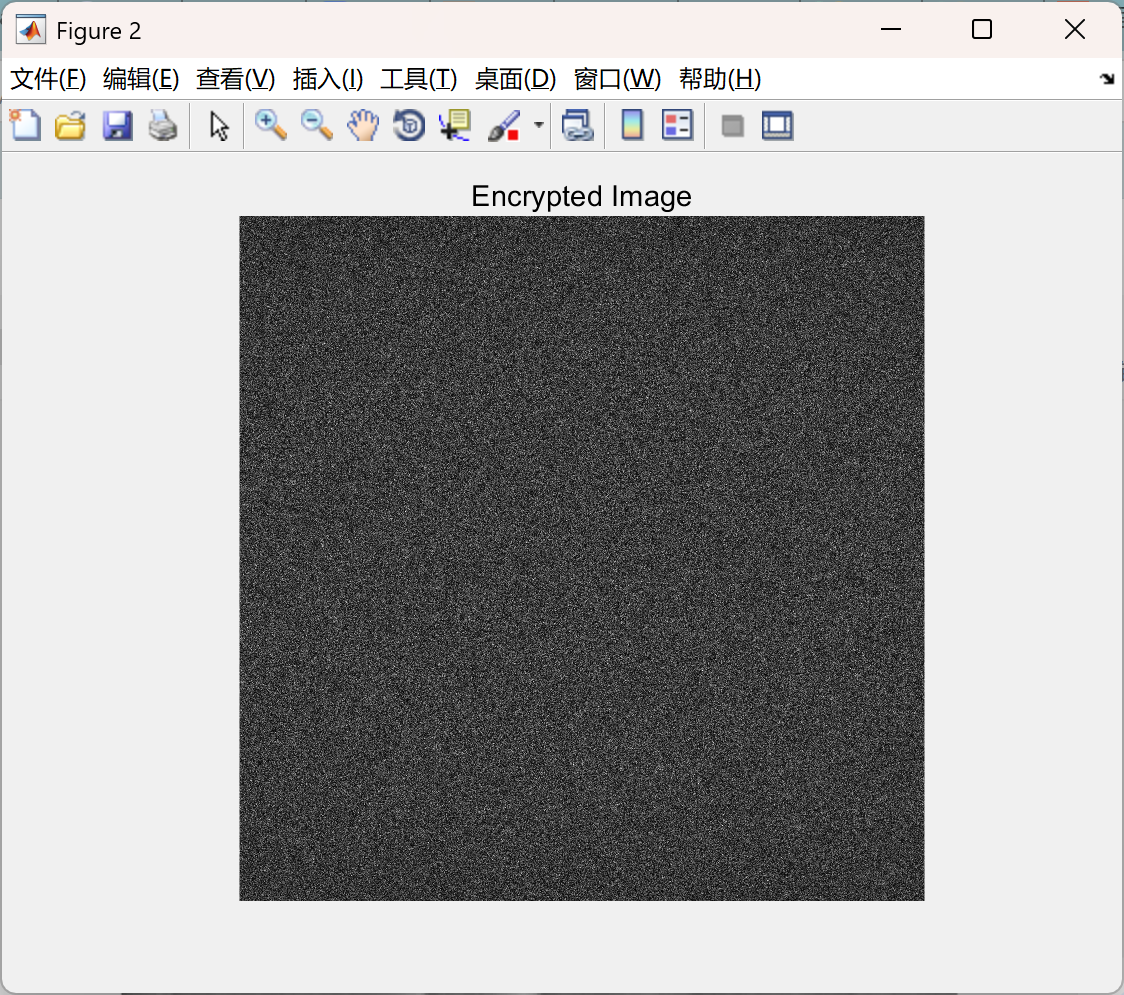
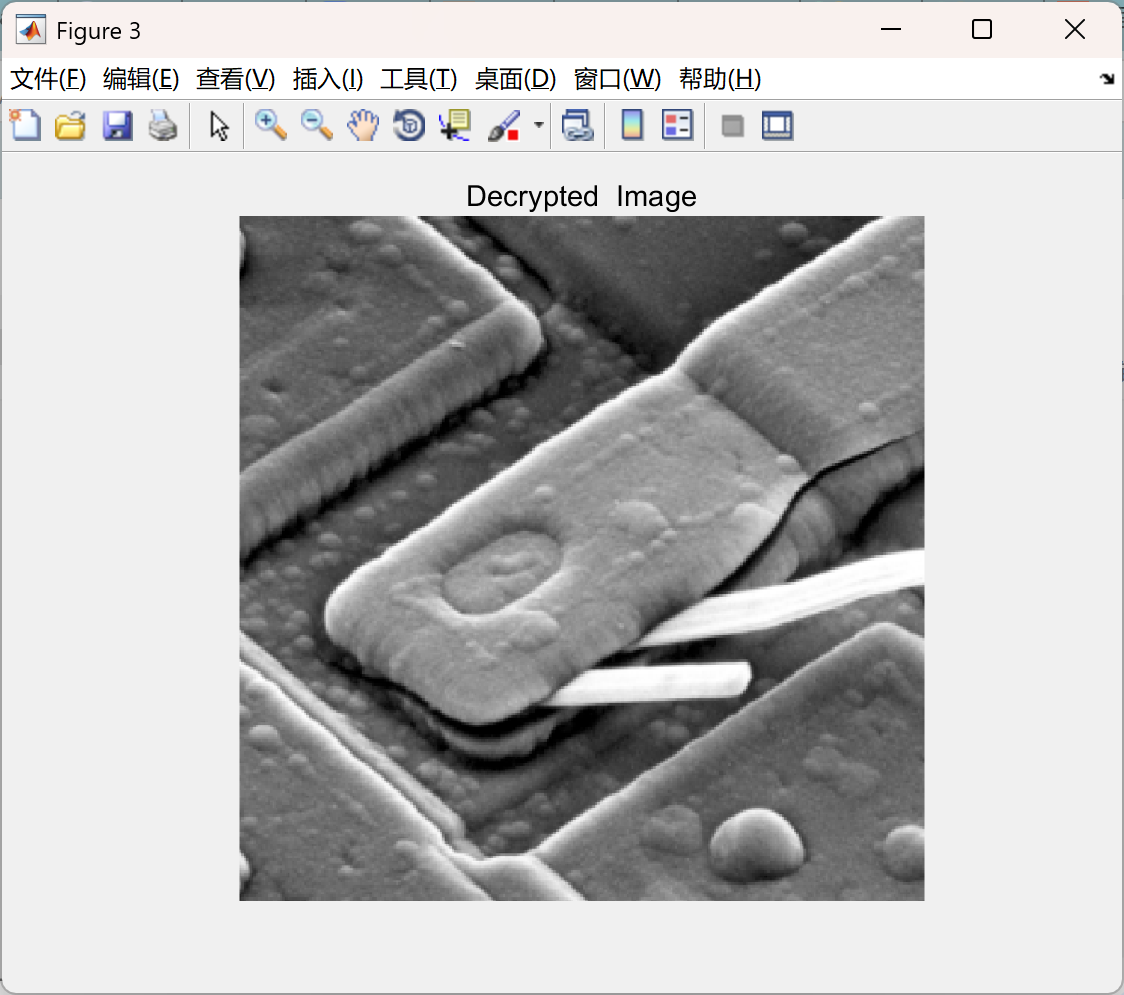
主函数部分代码：

clc; clear; close all;
%
imgFile = 'Fig0431(d)(blown_ic_crop).tif';
image = imread  (imgFile);
image =  im2double(image);

% Meaningful Patch size 3,6,9 % Patch increases the sceuirty of the
% encrypted picture

patchDim = 6;

[image_ps, mask] = randomPhaseShift(image);            % Step 1

[ ImageIndex, status ] = extractImageIndex(image_ps,patchDim);
patchIndex             = createPatchIndex(ImageIndex,patchDim);

%0.5 < a < 1.5
key.power               = [0.6,0.75,0.8;0.8,0.75,0.6];
% Generate encryption key

for i = 1 : 3
key.ScrambleIndex(i, :)  = randperm(patchDim^2,patchDim^2);
end

[encryptedImage ] = encryptImage(image_ps,patchDim,key);
[decryptedImage]  = decryptImage(encryptedImage,key,patchDim);


decryptedImage = abs(decryptedImage);
figure;
imshow(image,[],'InitialMagnification','fit')
title('Original Image');
figure;
imshow( abs(encryptedImage),[],'InitialMagnification','fit')
title('Encrypted Image');
figure;