【路径规划】ABC + PSO 路径规划（Matlab实现）

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/145146741

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、引言

路径规划是许多领域中的关键问题，例如机器人导航、自动驾驶、物流运输和无人机飞行等。ABC + PSO 路径规划是一种融合了人工蜂群算法（ABC）和粒子群优化算法（PSO）的创新型路径规划方法，旨在为各种应用场景提供更优的路径决策。

二、ABC 算法简介

人工蜂群算法（ABC）是一种模拟蜜蜂群体觅食行为的优化算法。在该算法中：蜜蜂角色划分：雇佣蜂：负责探索潜在的解空间，类似于寻找花丛的蜜蜂。它们会对当前解进行局部搜索，并将信息传递给观察蜂。观察蜂：依据雇佣蜂提供的信息，按照一定的概率选择并更新最优解，从而优化搜索过程。侦察蜂：在搜索陷入局部最优时，侦察蜂会随机生成新的解，防止算法停滞，保证搜索的多样性和全局性。算法优势：全局搜索能力强，通过侦察蜂的随机搜索机制，能够探索搜索空间的不同区域，避免过早陷入局部最优解。具有较好的鲁棒性，对于不同类型的优化问题都能展现出一定的适应性。

三、PSO 算法简介

粒子群优化算法（PSO）模拟了鸟群或鱼群的社会行为，具体表现为：粒子及其行为：每个粒子代表一个可能的解，具有位置和速度两个属性。粒子在搜索空间中运动，位置表示当前解，速度决定其运动方向和距离。粒子根据自身的历史最优位置（个体最优）和整个粒子群的历史最优位置（全局最优）更新自身的速度和位置，使其朝着最优解靠近。算法优势：收敛速度快，能够在较短的迭代次数内找到较优的解，适合对计算时间有限制的场景。算法结构简单，易于实现和调整参数，对于简单到中等复杂程度的优化问题有良好的效果。

四、ABC + PSO 路径规划原理

结合思路：优势互补：ABC 算法的全局搜索能力和 PSO 算法的快速收敛特性相结合，在路径规划中可以实现更高效的优化。ABC 可以在广阔的解空间中广泛搜索，避免陷入局部最优；PSO 则可对已找到的较优区域进行快速精细搜索，加快找到最优路径的速度。协同工作：两种算法可以并行或串行工作，并行时它们可同时对解空间进行探索和优化，相互提供信息；串行时可先使用 ABC 算法进行全局搜索，再用 PSO 算法进行局部优化，或者反之。应用场景：在复杂环境中，如机器人在障碍物密集的环境中寻找从起点到终点的路径，ABC + PSO 可以考虑到更多的路径可能性，避免局部陷阱，同时快速找到最优或接近最优的路径。在自动驾驶领域，能根据路况、交通规则和车辆性能，规划出最优的行驶路线，提高行驶效率和安全性。对于物流配送，根据不同的配送点、交通状况和时间限制，规划出最经济、高效的运输路线。

五、结论

ABC + PSO 路径规划综合了人工蜂群算法和粒子群优化算法的优势，为解决复杂的路径规划问题提供了一种强大的工具。它在多种领域展现出巨大的潜力，不仅能提升路径规划的质量，还能适应不同的环境约束和性能要求。未来，随着算法的不断改进和参数调整，ABC + PSO 路径规划有望在更多领域得到广泛应用，为路径规划带来更加智能和高效的解决方案。通过这种结合，我们可以克服单一算法的局限性，提高算法在复杂场景下的适应性和性能，为路径规划领域带来新的突破和发展，满足现代社会对智能路径规划日益增长的需求。

📚2 运行结果

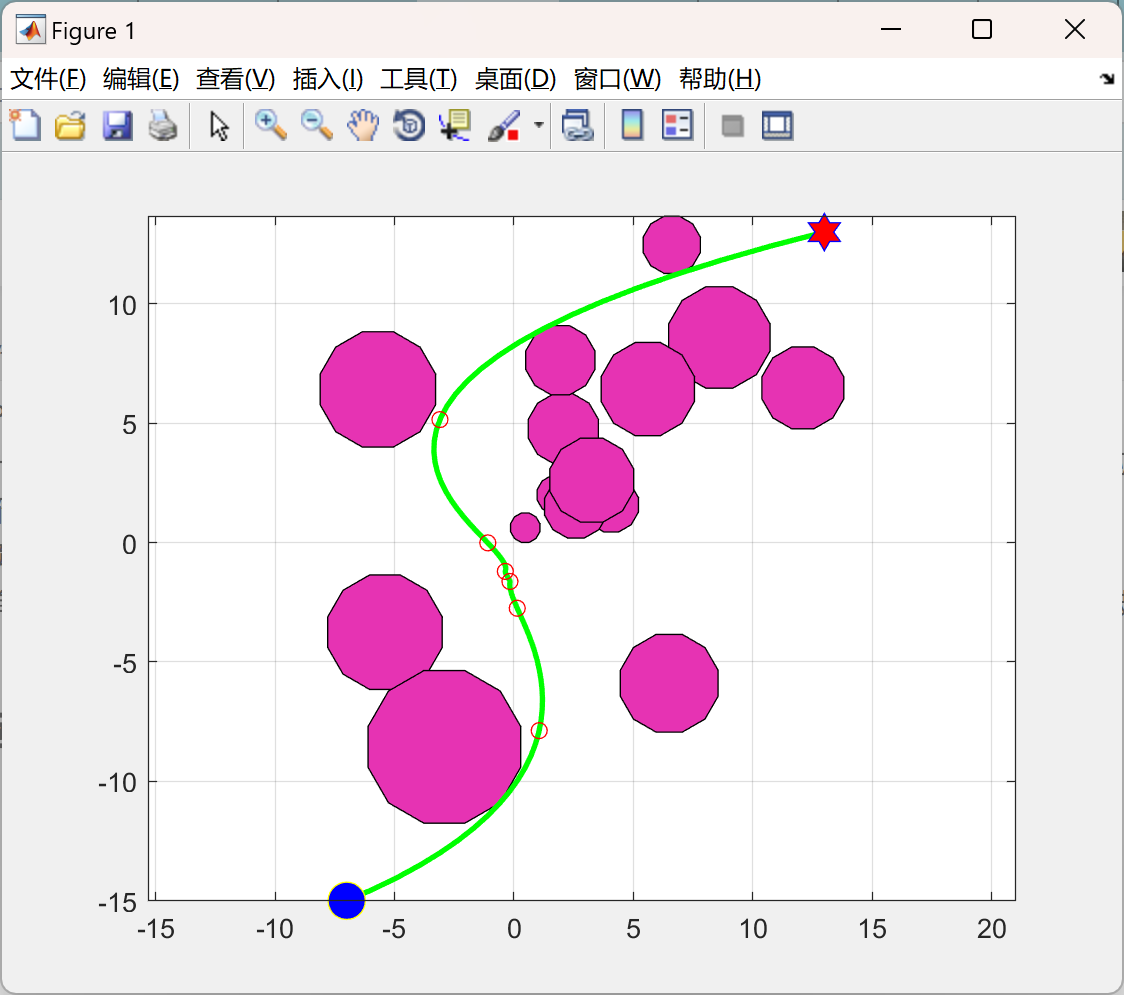
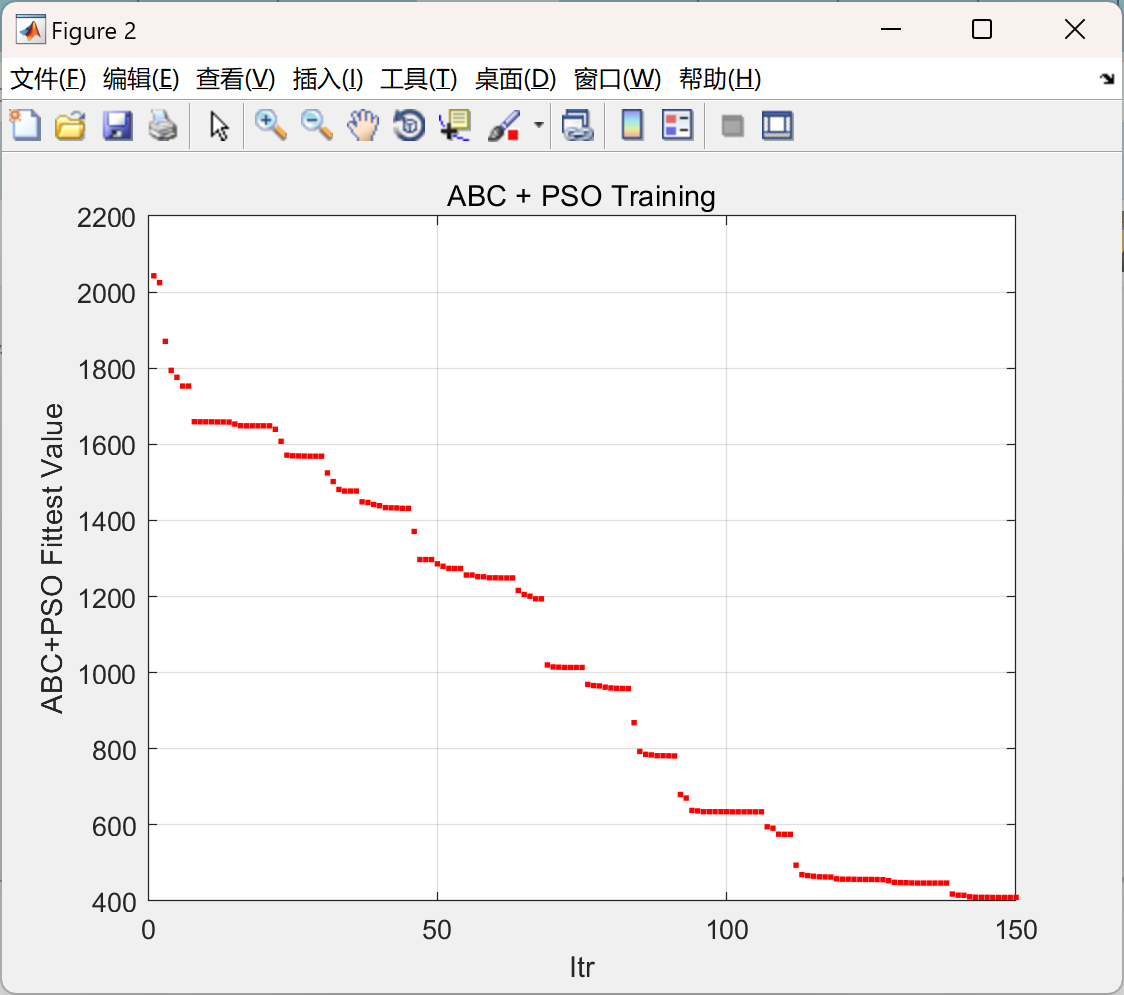
主函数部分代码：


%% Cleaning The Stage
clc;
clear;
warning('off');

%% Start ABC + PSO Optimal Path Finder
model=Basics();
model.n=6;  % number of Handle Points
CostFunction=@(x) Cost(x,model);    % Cost Function
nVar=model.n;       % Number of Decision Variables
VarSize=[1 nVar];   % Size of Decision Variables Matrix
VarMin.x=model.xmin;           % Lower Bound of Variables
VarMax.x=model.xmax;           % Upper Bound of Variables
VarMin.y=model.ymin;           % Lower Bound of Variables
VarMax.y=model.ymax;           % Upper Bound of Variables

%% PSO + ABC Parameters
MaxIt=150;          % Maximum Number of Iterations
nPop=20;           % Population Size (Swarm Size)
w=1;                % Inertia Weight
wdamp=0.98;         % Inertia Weight Damping Ratio
c1=1.5;             % Personal Learning Coefficient
c2=1.5;             % Global Learning Coefficient
nOnlooker = nPop;         % Number of Onlooker Bees
L = round(0.6*nVar*nPop); % Abandonment Limit Parameter (Trial Limit)
a = 1;
alpha=0.1;
VelMax.x=alpha*(VarMax.x-VarMin.x);    % Maximum Velocity
VelMin.x=-VelMax.x;                    % Minimum Velocity
VelMax.y=alpha*(VarMax.y-VarMin.y);    % Maximum Velocity
VelMin.y=-VelMax.y;                    % Minimum Velocity

%% Initialization PSO + ABC
% Create Empty Particle Structure
empty_particle.Position=[];
empty_particle.Velocity=[];
empty_particle.Cost=[];
empty_particle.Sol=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
empty_particle.Best.Sol=[];
% Empty Bee Structure
empty_bee.Position = [];
empty_bee.Cost = [];
% Initialize Global Best
GlobalBest.Cost=inf;
% Initialize Population Array
pop = repmat(empty_bee, nPop, 1);
bee = repmat(empty_bee, nPop, 1);
% Initialize Best Solution Ever Found
BestSol.Cost = inf;
GlobalBest.Cost=inf;
% Create Particles Matrix
particle=repmat(empty_particle,nPop,1);
% Initialization Loop
for i=1:nPop
% Initialize Position
if i > 1
particle(i).Position=CRSolution(model);
else
% Straight line from source to destination
xx = linspace(model.xs, model.xt, model.n+2);
yy = linspace(model.ys, model.yt, model.n+2);
particle(i).Position.x = xx(2:end-1);
particle(i).Position.y = yy(2:end-1);
end
% Initialize Velocity
particle(i).Velocity.x=zeros(VarSize);
particle(i).Velocity.y=zeros(VarSize);
% Evaluation
[particle(i).Cost, particle(i).Sol]=CostFunction(particle(i).Position);
% Update Personal Best
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Sol=particle(i).Sol;
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
end
end
% Initialization Loop
for i=1:nPop
% Initialize Position
if i > 1
pop(i).Position=CRSolution(model);
else
% Straight line from source to destination
xx = linspace(model.xs, model.xt, model.n+2);
yy = linspace(model.ys, model.yt, model.n+2);
pop(i).Position.x = xx(2:end-1);
pop(i).Position.y = yy(2:end-1);