【滤波追踪】扩展卡尔曼滤波三维跟踪对象（Matlab实现）_imm扩展卡尔曼滤波三维路径跟踪-优快云博客

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/139780537

“在代码的海洋里，有无尽的知识等待你去发现。我就是那艘领航的船，带你乘风破浪，驶向代码的彼岸。

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

扩展卡尔曼滤波在三维对象跟踪中发挥着重要作用。首先，介绍了三维跟踪对象的应用场景，如在航空航天、自动驾驶、虚拟现实和机器人技术等领域中对物体位置、速度和姿态的实时监测和追踪。阐述了扩展卡尔曼滤波的基本原理和算法，它通过对系统状态的预测和测量更新来估计对象的动态特性。在三维空间中，需要考虑对象的三个位置坐标以及可能的速度、加速度等多个状态变量。详细讨论了如何建立三维跟踪对象的数学模型，包括运动模型和观测模型。运动模型描述对象在三维空间中的运动规律，观测模型则将传感器获取的测量数据与对象的状态相关联。分析了扩展卡尔曼滤波在处理非线性系统时的优势和局限性，以及为了提高跟踪精度和稳定性所采取的改进措施。最后，通过实验和实际应用案例展示了扩展卡尔曼滤波在三维对象跟踪中的性能表现，并对未来的发展趋势和研究方向进行了展望。扩展卡尔曼滤波为实现准确、可靠的三维对象跟踪提供了一种有效的方法和技术手段。

📚2 运行结果

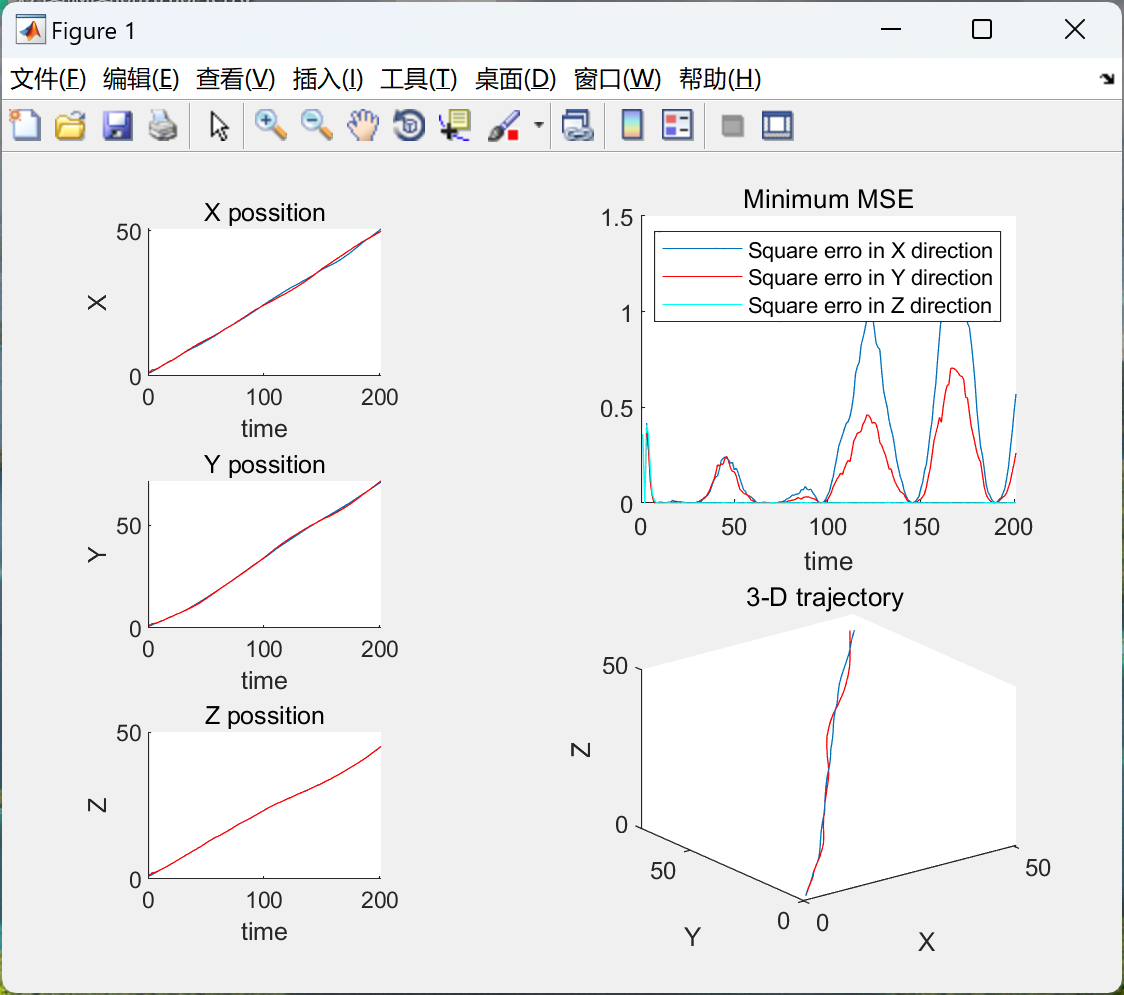
部分代码：

%estimating trajectory of an object in 3-D
function ExtendedKalmanFilter
clc, clear all, clf

Q=[0 0 0 0 0 0;
   0 0 0 0 0 0;
   0 0 0 0 0 0;
   0 0 0 0.01 0 0;
   0 0 0 0 0.01 0;
   0 0 0 0 0 0.01];% Covarience matrix of process noise 


M=[0.001 0 0;
    0 0.001 0;
    0 0 0.001]; % Covarience matrix of measurment noise 


d=.1;% sampling time 

A=[1 0 0 d 0 0;
   0 1 0 0 d 0;
   0 0 1 0 0 d;
   0 0 0 1 0 0;
   0 0 0 0 1 0;
   0 0 0 0 0 1]; % System Dynamics 

X(:,1)=[1;1;1;2;2;2]; % Actual initial conditions 



Z(:,1)=[3;3;3];% initial observation 


Xh(:,1)=[1.6;1.6;1.6;20;20;20];%Assumed initial conditions

P(:,:,1)=[0.1 0 0 0 0 0;
          0 0.1 0 0 0 0;
          0 0 0.1 0 0 0;
          0 0 0 0.1 0 0;
          0 0 0 0 0.1 0;
          0 0 0 0 0 0.1]; %inital value of covarience of estimation error
  
%
   


% Setting up plots 
subplot(3,3,1)
xlabel('time') 
ylabel('X')
title('X possition')
hold on