💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
背包问题是计算机科学和组合优化中的经典优化问题。它涉及找到最有价值的物品组合,以适应具有有限容量的背包。该问题通常由一组物品定义,每个物品具有重量和价值,并且具有最大重量容量的背包。目标是在确保总重量不超过背包容量的情况下,最大化背包中物品的总价值。背包问题在资源分配、投资组合优化和物流规划等实际场景中具有各种应用。背包问题有不同的变体,包括 0/1 背包问题(物品不可分割)和分数背包问题(物品可分割为分数)。使用各种算法,如动态规划、贪婪算法和分支定界技术,可以高效解决不同版本的背包问题。
📚2 运行结果
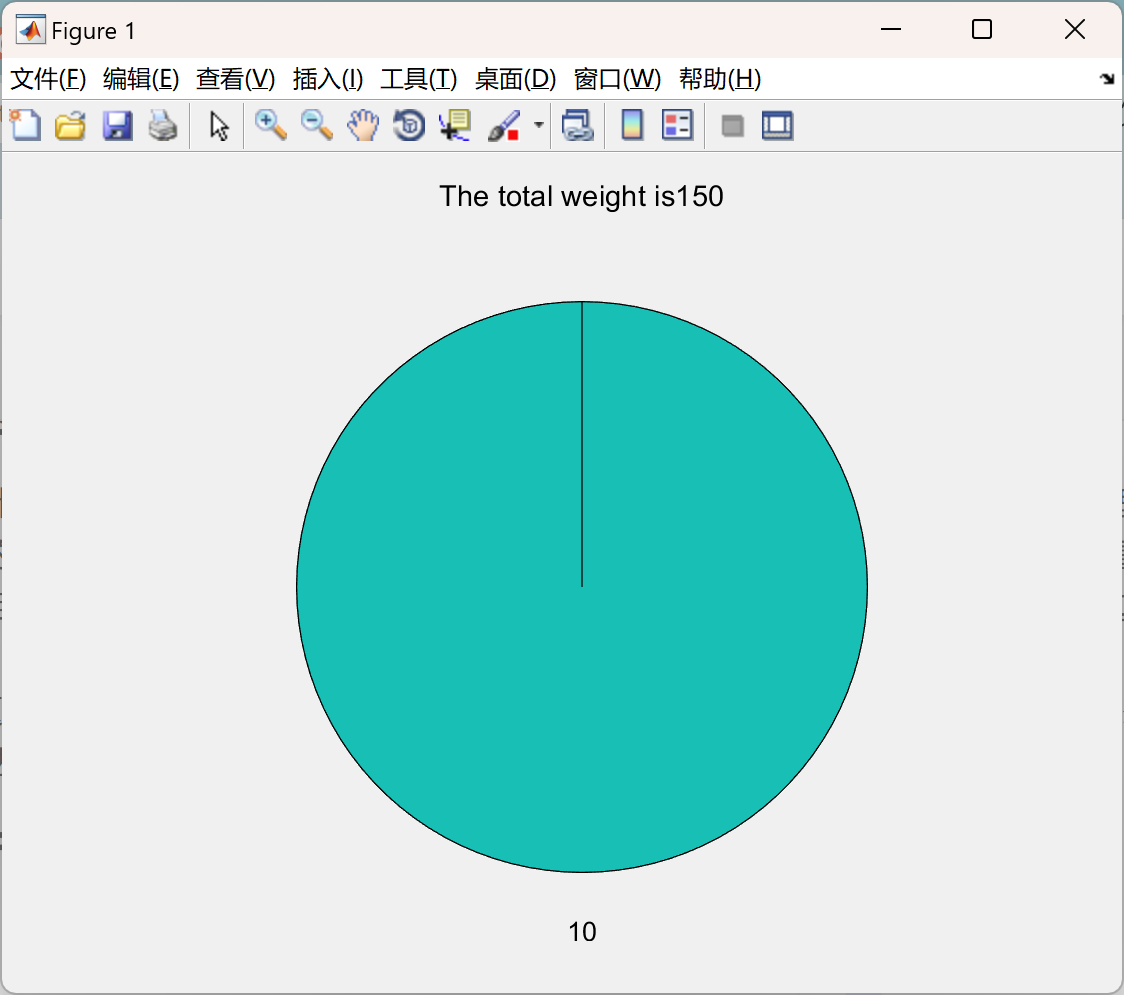
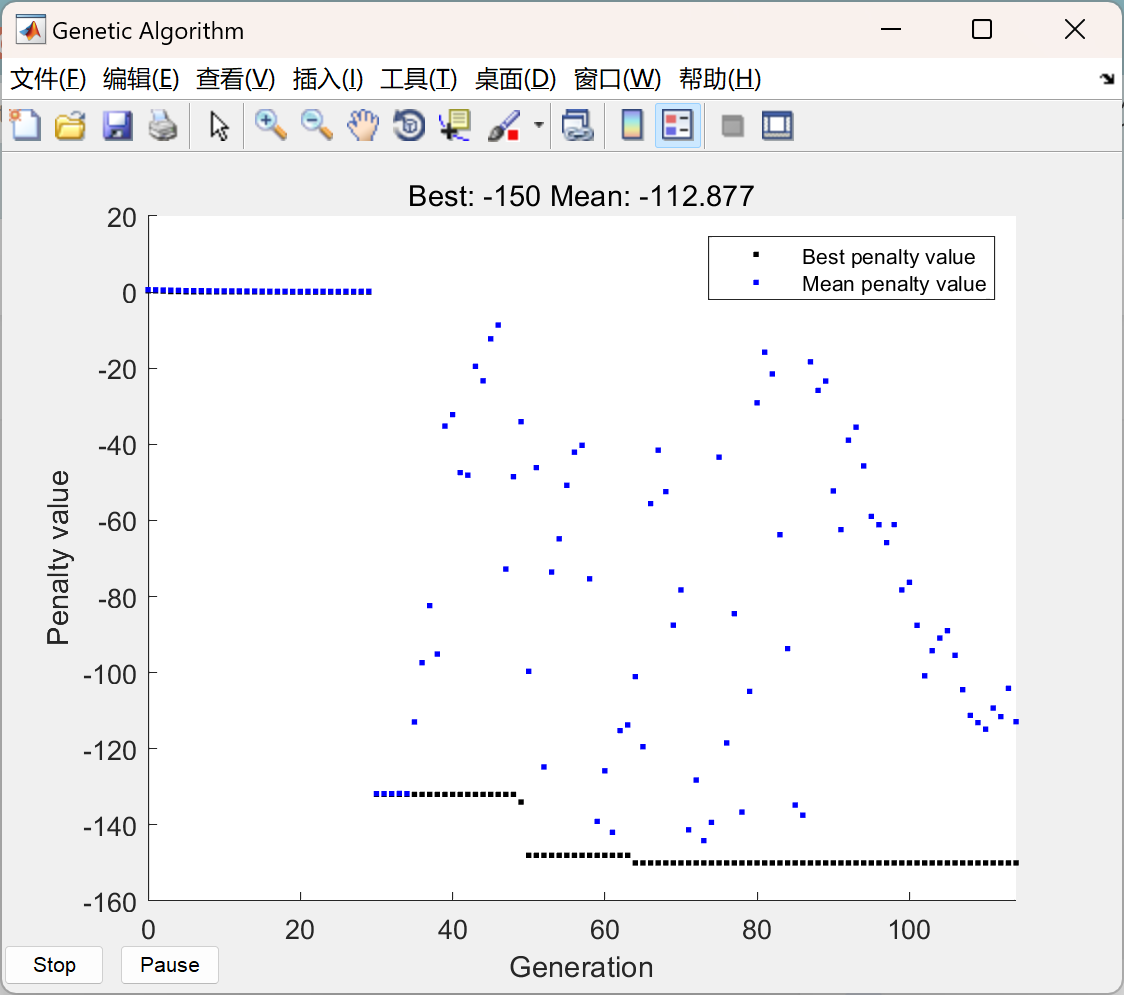
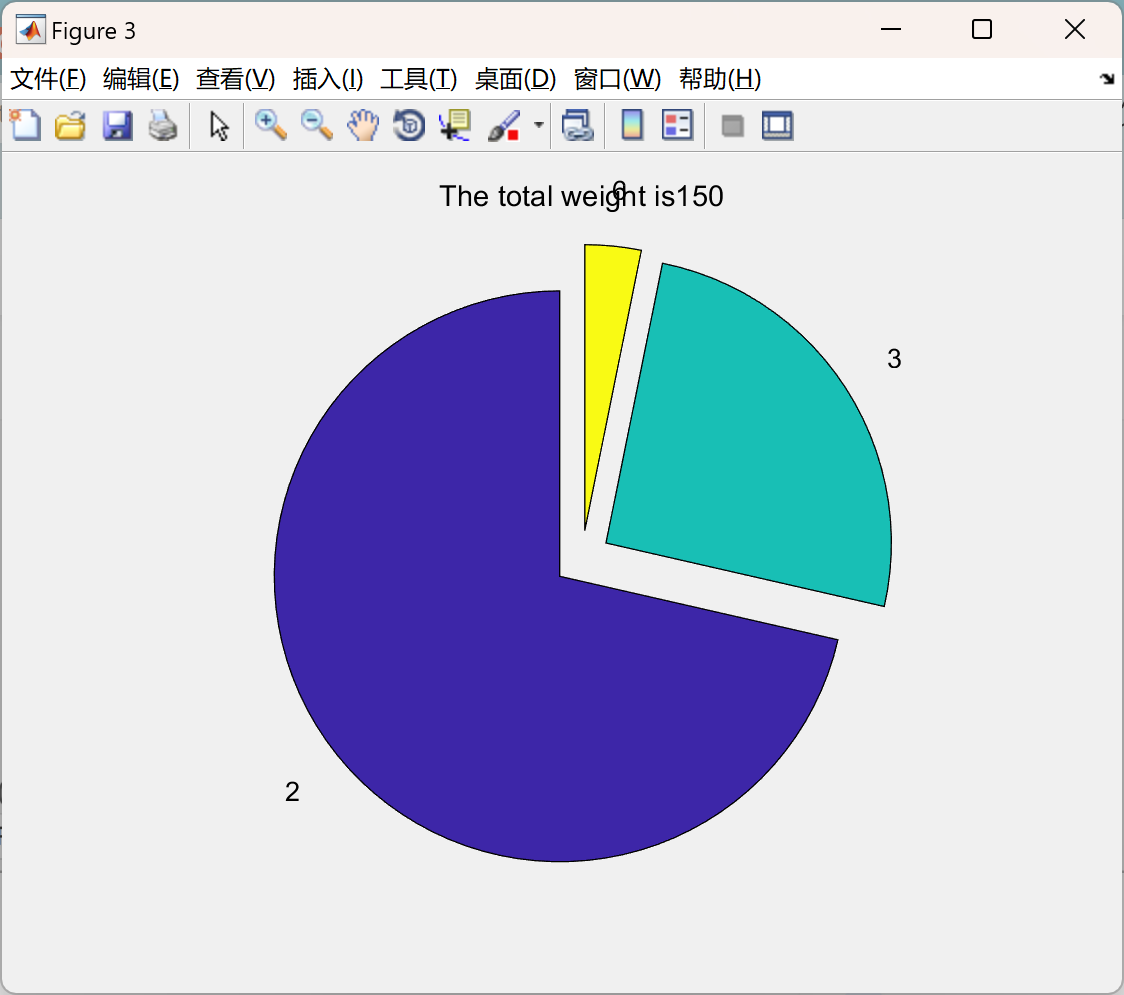
部分代码:
function knapsackGA
%% The knapsack problem
% The knapsack problem or rucksack problem is a problem in combinatorial optimization:
% Given a set of items, each with a weight and a value, determine the count of each
% item to include in a collection so that the total weight is less than or equal to a
% given limit and the total value is as large as possible. It derives its name from
% the problem faced by someone who is constrained by a fixed-size knapsack and must
% fill it with the most useful items.
%
% The problem often arises in resource allocation with financial constraints. A
% similar problem also appears in combinatorics, complexity theory, cryptography and
% applied mathematics.
%
% The decision problem form of the knapsack problem is the question "can a value of
% at least V be achieved without exceeding the weight W?"
%% Linear programing first
w=1:10;
sumOfAllItemsInSack=150;
options=optimset('Display','off','LargeScale','off');
[x,fval]=linprog(-w,w,sumOfAllItemsInSack,[],[],zeros(1,length(w)),[],...
sumOfAllItemsInSack./(ones(1,length(w))*length(w)),options);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]Galli L ,Letchford N A . On upper bounds for the multiple knapsack assignment problem[J]. Operations Research Letters,2024,54.
[2]Jean L A ,Brauner N ,Briant O , et al. Stability constraints in a 3D knapsack problem with non parallelepipedic items[J]. Computers & Industrial Engineering,2024,189.




 本文探讨了背包问题这一经典的计算机科学优化问题,介绍了其在实际应用中的重要性,以及不同版本(0/1背包和分数背包)的特性。文章还提供了使用Matlab进行线性规划求解背包问题的示例代码。
本文探讨了背包问题这一经典的计算机科学优化问题,介绍了其在实际应用中的重要性,以及不同版本(0/1背包和分数背包)的特性。文章还提供了使用Matlab进行线性规划求解背包问题的示例代码。
















 2354
2354

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








