路径规划的概率算法

最新推荐文章于 2025-01-13 11:25:27 发布

原创最新推荐文章于 2025-01-13 11:25:27 发布 · 1.1k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#算法

本文介绍了Rapidly-exploringRandomTrees(RRT)算法在处理有障碍物的高维空间中的路径规划，包括工作原理、随机采样与连接策略，以及使用Matlab实现的示例代码。通过实例展示了如何在复杂的环境中寻找可行路径。

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

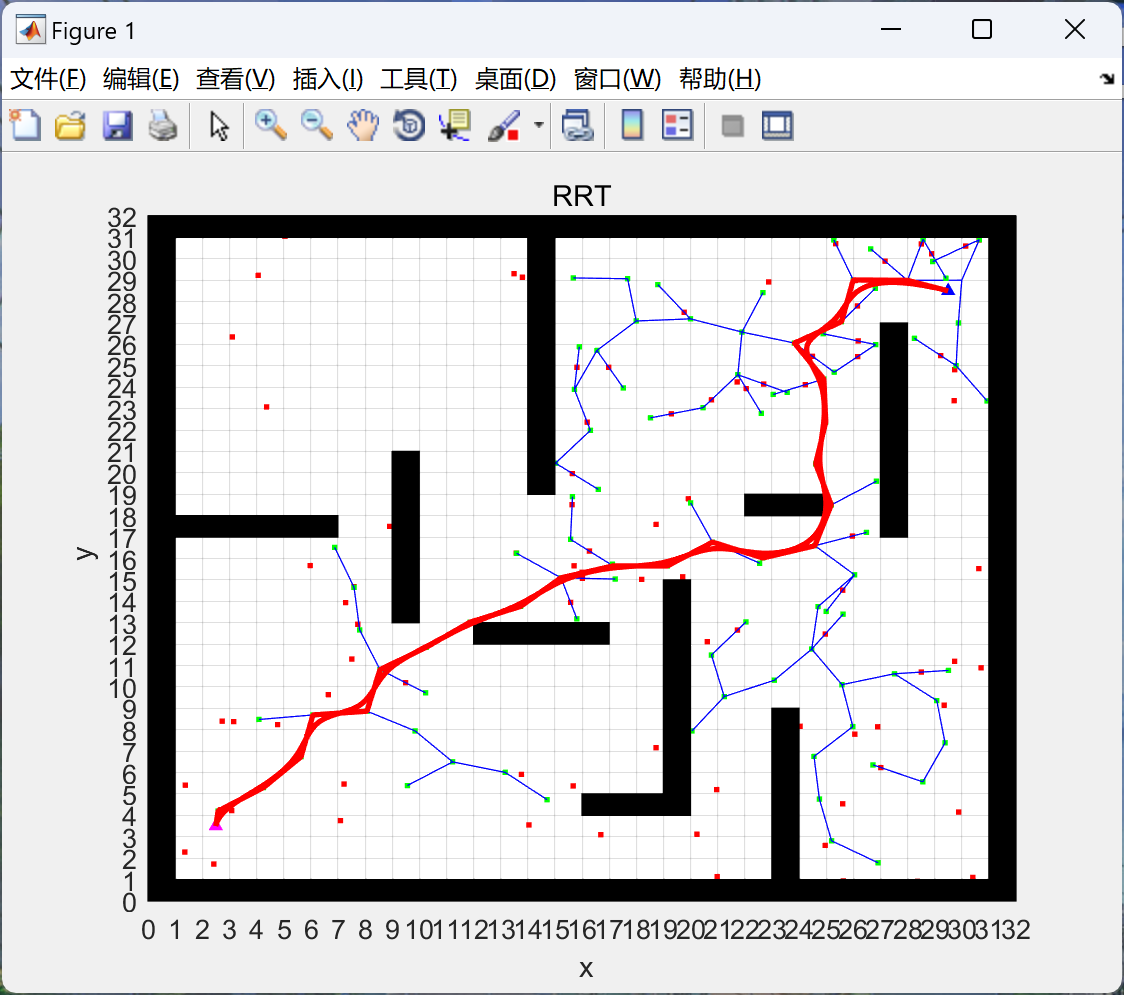
用于路径规划的快速探索随机树（RRT）算法的工作原理是构建一个探索机器人配置空间的树，根节点代表初始配置，并通过随机采样和与现有树的连接迭代添加新节点。该算法使用距离度量来标识树中离每个新采样点最近的节点，如果它们之间的连接不与障碍物相交，则向树中添加新节点和边。随着树的生长，它会探索配置空间的更多区域并接近目标配置。当达到目标或达到定义的迭代次数限制时，算法将终止。RRT 可以处理有障碍物的高维和复杂空间，但由于采样过程的随机性，可能并不总是找到最佳路径。

📚2 运行结果

部分代码：

% [1] LaValle S M. Rapidly-exploring random trees: A new tool for path planning[J]. 1998.
% If you use the code, please make sure that you cite references [1].
% Lixing Liu and Xin Yang
% Emails: 1135337497@qq.com

clc
clear
close all

extend_area = 0.2;
resolution = 1;
robot_radius = 0.5;

ob2 = [1,18,6,0];
ob3 = [10,14,0,7];
ob4 = [13,13,4,0];
ob5 = [15,20,0,11];
ob6 = [17,5,3,0];
ob7 = [20,5,0,10];
ob8 = [24,1,0,8];
ob9 = [23,19,2,0];
ob10 = [28,18,0,9];


ob_limit_1 = [1,1,0,31];
ob_limit_2 = [1,1,31,0];
ob_limit_3 = [32,1,0,31];
ob_limit_4 = [1,32,31,0];
ob = [ob2;ob3;ob4;ob5;ob6;ob7;ob8;ob9;ob10;...
      ob_limit_1;ob_limit_2;ob_limit_3;ob_limit_4];
  

x_left_limit = 0; 
x_right_limit = 32;
y_left_limit = 0;
y_right_limit = 32;


extend_area = 0.2;
resolution = 1;
robot_radius = 0.2;

x_start = [30, 29];
goal = [3, 4];

grow_distance = 2; 
goal_radius = 1.5;


tree.child = [];
tree.parent = [];
tree.child = x_start;

flag = 1;

new_node_x = x_start(1,1);
new_node_y = x_start(1,2);
new_node = [new_node_x, new_node_y];

tic             
while true
    rd_x = 32 * rand();   
    rd_y = 32 * rand();    
    if (rd_x >= x_right_limit || rd_x <= x_left_limit ||... 
        rd_y >= y_right_limit || rd_y <= y_left_limit)
        flag = 0;
    end
    
    [angle, min_idx] = cal_distance(rd_x, rd_y, tree);   
    new_node_x = tree.child(min_idx,1)+grow_distance*cos(angle);
    new_node_y = tree.child(min_idx,2)+grow_distance*sin(angle);
    new_node = [new_node_x, new_node_y];
    
    for k=1:1:size(ob,1) 
        for i=min(tree.child(min_idx,1),new_node_x):0.01:max(tree.child(min_idx,1),new_node_x)    
            j = (tree.child(min_idx,2) - new_node_y)/(tree.child(min_idx,1) - new_node_x) *(i - new_node_x) + new_node_y;
            if(i >=ob(k,1)-resolution && i <= ob(k,1)+ob(k,3) && j >= ob(k,2)-resolution && j <= ob(k,2)+ob(k,4))
                flag = 0;
                break
            end
        end
    end