在地形上寻找最佳路径（matlab实现）

最新推荐文章于 2025-12-10 11:08:55 发布

原创最新推荐文章于 2025-12-10 11:08:55 发布 · 442 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#matlab

本文探讨了车辆行驶过程中如何通过避开上升和下降轨迹，采用成本函数最小化策略来实现目标坐标最短路径和最短旅行时间。内容包括行驶规则、避免策略以及用Matlab的实际代码示例。

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

车辆在行驶过程中必须尽可能接近目标坐标，并确保旅行时间最短。每次移动车辆只能沿着八个方向之一进行：左、右、上、下、左上、左下、右上和右下。
成本函数被定义为海拔高度的差异，始终为正数。在行驶过程中，车辆必须避免沿着上升轨迹行驶。然而，沿着下降轨迹行驶对车辆也没有好处。因此，下降轨迹并不比平坦轨迹更可取。在这个过程中，车辆的导航旨在最大程度地降低成本函数，以实现高效且迅速的目标达成。

📚2 运行结果

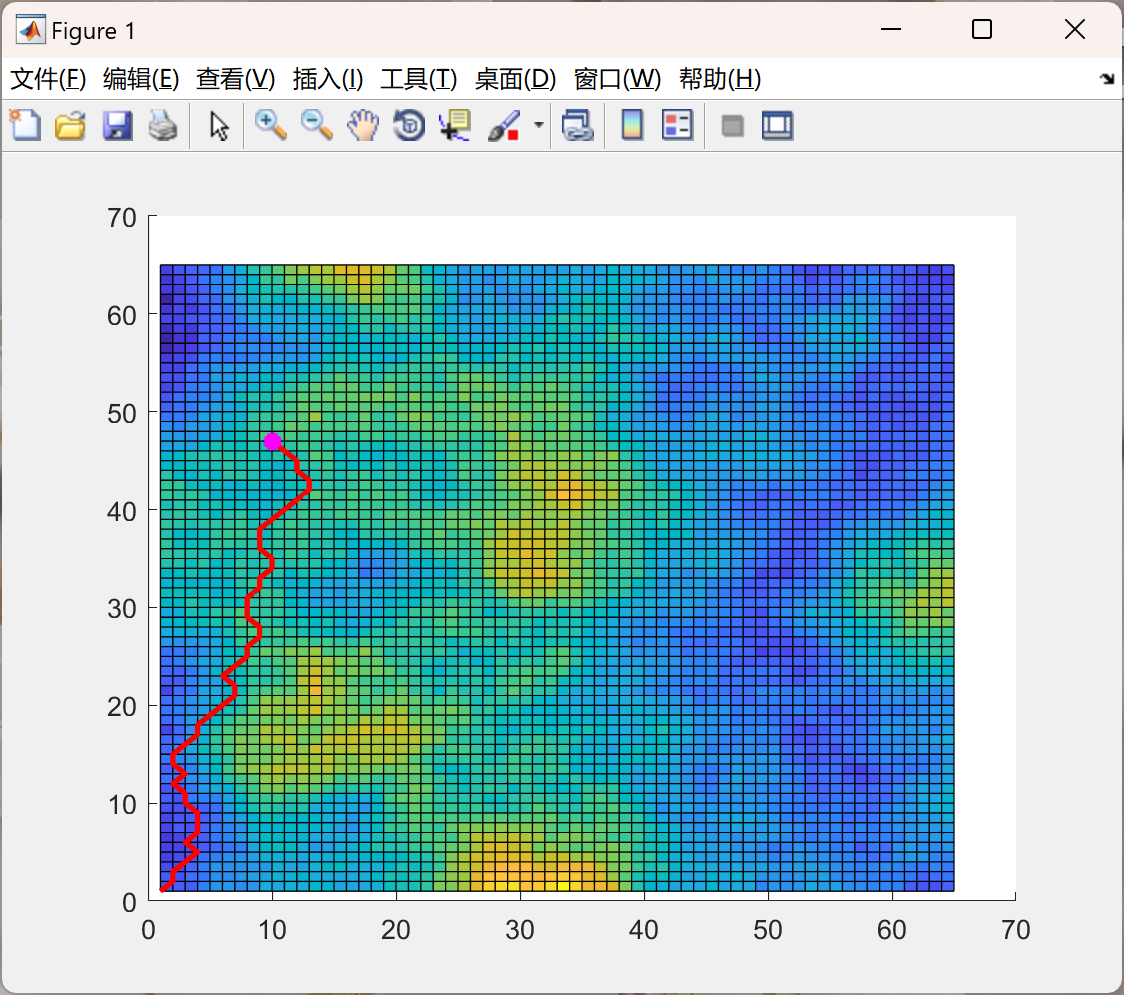
🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]Miri M S ,Riahi T H ,Mahmoudy A S . Uniform deformation distribution of structures at different seismic hazard levels using endurance time method[J]. Structures,2024,60.

[2]Zeng C ,Yang T ,Wang Z , et al. Functional-group-regulated stimuli-responsive banana-shaped α-cyanostilbene derivatives: Dual-state emission, AIEE, acidochromism and their applications in anti-counterfeiting, fingerprint recognition and OLEDs[J]. Journal of Luminescence,2024,269.