【风险敏感控制、随机最优控制】在优化机器人控制中考虑不确定性通过高阶成本统计研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章下载

---

💥1 概述

摘要—随着概率模型在机器人应用中的增加，一种考虑不确定性影响的系统化机器人控制方法变得不可或缺。受人类感觉运动发现的启发，本文研究了具有高阶成本统计的随机最优控制问题，以合成在具有多个不确定性来源的机器人场景中依赖于不确定性的行动。我们提出了非线性动力学、多个附加不确定性来源和非二次成本设置的局部最优风险敏感和成本累积解决方案。每个不确定性来源对成本的影响可以被单独参数化，为控制设计提供了额外的灵活性。我们进一步分析了静态不确定参数参与的情况。对几个具有非二次成本的线性和非线性设置的模拟以及对真实机器人平台的实验验证了我们的方法，并展示了其独特性。

关键词—风险敏感控制、随机最优控制、机器人控制中的不确定性。

智能系统的核心能力之一是对环境中的不确定性做出适当反应，这一点自80年代末以来在人工智能中就得到了认可[1]。虽然现代推理方法以复杂的方式接纳了随机不确定性，但低层次的机器人控制仍然缺乏合适的方法。最先进的随机控制方法考虑了期望值，却忽视了高阶统计量。本文的目标是通过提供一种系统化的方法，填补概率建模方法和机器人控制之间的差距，以便在随机不确定性的情况下提供机器人控制的系统化方法，超越一阶统计量。例如，考虑一项具有不确定姿势的抓取任务。其期望值只是其概率表示的粗略估计。然而，其方差可能在某些自由度上表现出更多的确定性，针对这些自由度更积极地设计控制，同时允许其他自由度更多的变化可能是任务成功的关键。同样，如果我们考虑在拥挤环境中的导航任务，障碍物的不确定性水平不同，那么碰撞的可能性可能会因障碍物姿势的方差而有显著变化。这些简单的原型示例说明了需要一种系统化和灵活的控制方法，以考虑机器人环境中的不确定性。

由于人类在各种任务上成功的能力，人类行为成为机器人控制设计的可靠灵感来源。近年来，神经科学家研究了人类感觉运动控制，强调了他们克服甚至受益于噪音和不确定性影响的能力[2]。特别是，在这一领域的结果显示，人类运动控制可以被建模为考虑动力学中的噪声的最优控制问题[3]。这些发现激发了许多用于机器人控制的随机最优控制方法，这些方法最小化了随机成本的期望值[4]，[5]。然而，最近的结果通过风险敏感最优控制来解释人类行为[6]。直观地说，风险敏感的决策者在面对不确定性时偏离期望最优解，不仅考虑随机成本的期望值，还考虑其方差和更高阶统计量（矩或累积量）。

📚2 运行结果

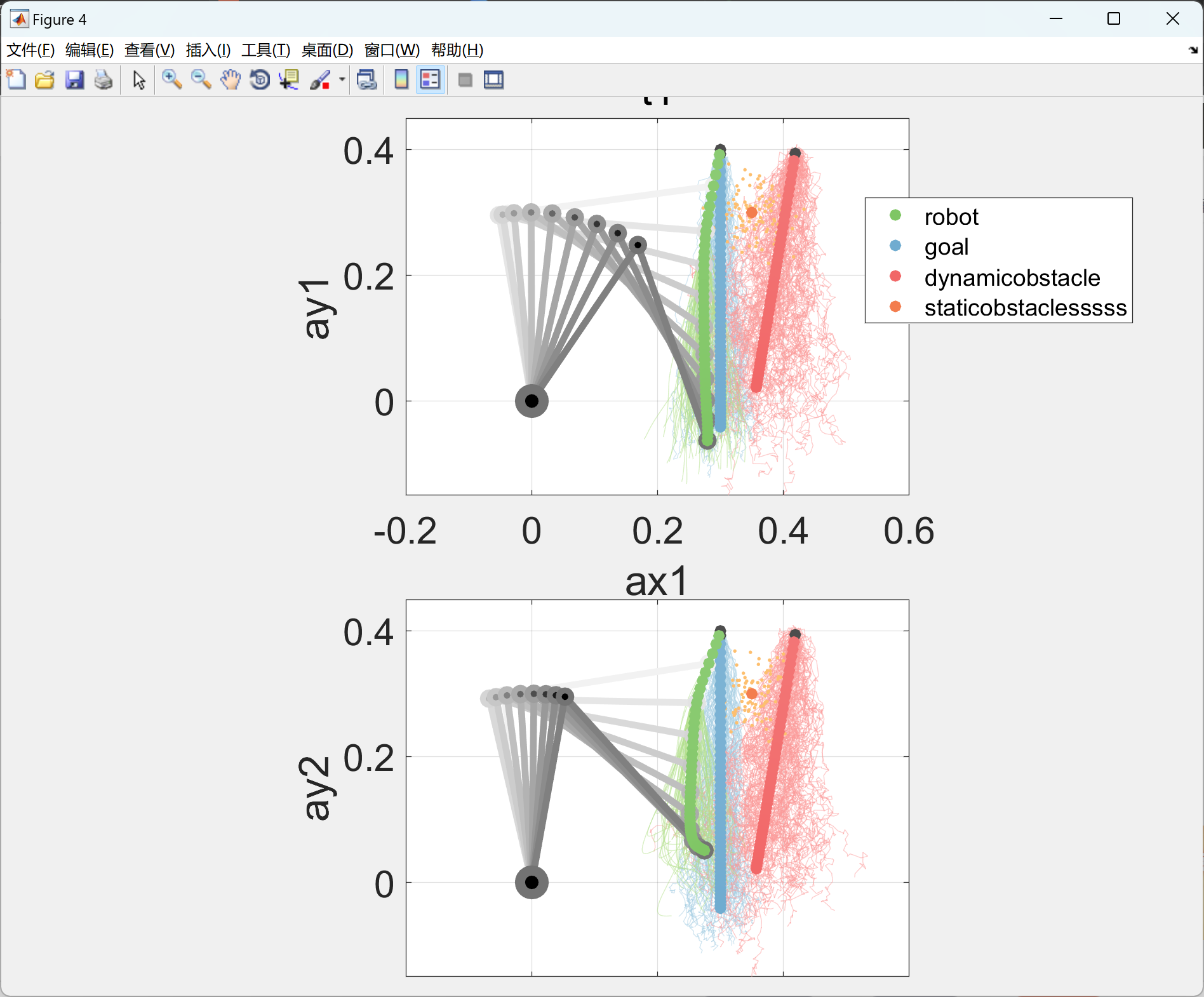
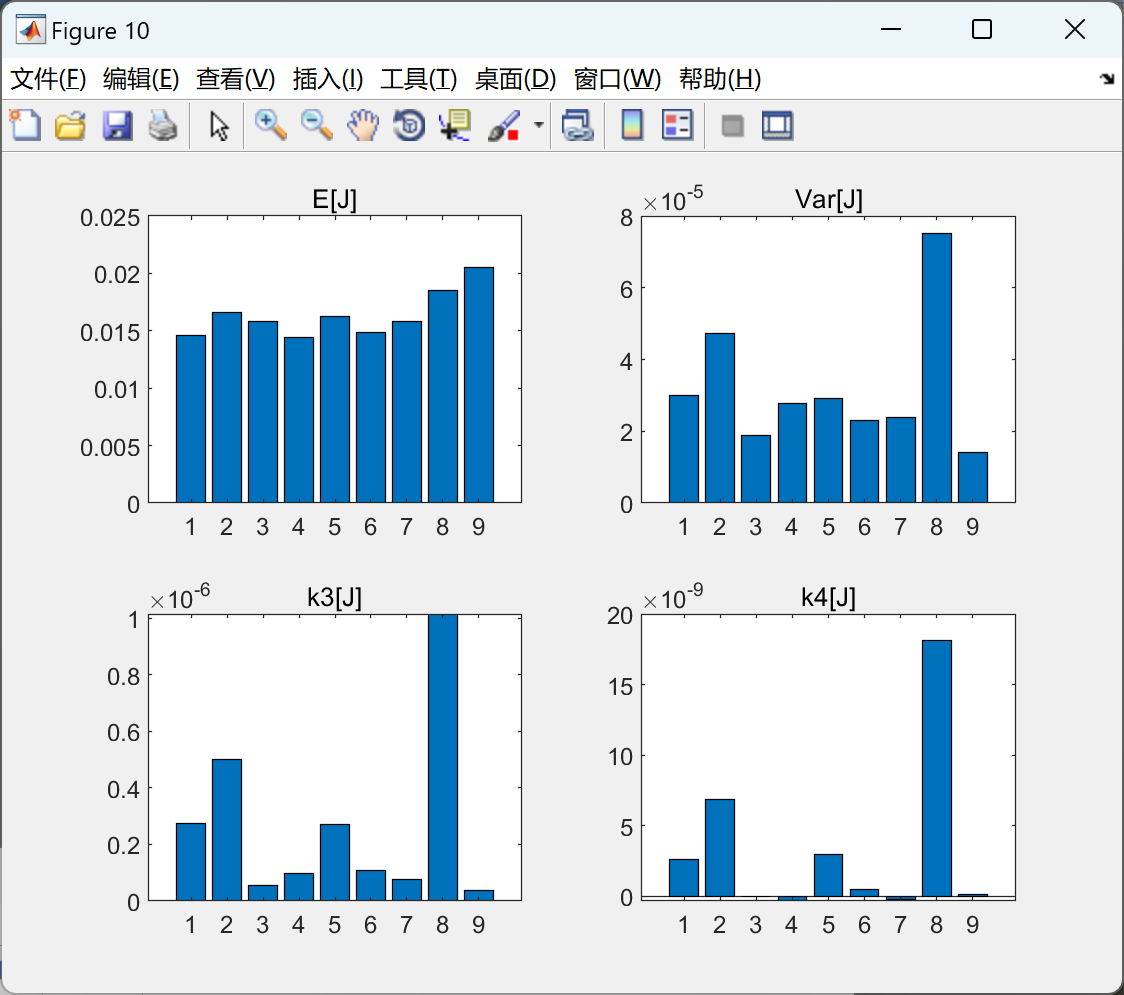
部分代码：

%%  Optimization parameters
T = 200;
dt = 0.01;
u0 = zeros(2,1);
max_iter = 1000;
uMin = -Inf;
uMax = Inf;

% Initial states
x_rob = [0 0 0 0]';
x_goal = [0.1 0.1 1 -0.5]';
x_obs = [0.15 0.15 1 -0.5]';
x0 = [x_rob ; (x_goal - x_rob) ; (x_obs - x_rob)];

% Static obstacles: position and Sigma
sobs_pos = [0.8 -0.3 ; 0.8 -0.6]';
sobs_Sigma(:,:,1) =  0.001*eye(2);
sobs_Sigma(:,:,2) =  0.005*eye(2);

% Cost function
costWithObstacles = ...
    @(x, u , t) pointMass_dyngoalobsfull_cost(x, u, t, sobs_pos, sobs_Sigma);
costWithoutObstacles = ... % For initialization
    @(x, u , t) pointMass_dyngoalobsfull_cost(x, u, t, [], []);

% Dynamics function
dynamics_function = @pointMass_dyngoalobsfull_dyn;

% Plot functions
plotWithoutObstacles = ...
    @(x, u , L, varargin) pointMass_dyngoalobsfull_plot(x, u, L, ...
                                                        [], [], varargin{:});
plotWithObstacles = ...
    @(x, u , L, varargin) pointMass_dyngoalobsfull_plot(x, u, L, ...
                                          sobs_pos, sobs_Sigma, varargin{:});

% Define LQ solvers
gamma_neg = 2;
gamma_pos = 4;
ExpectedCost = @(lqProb, varargin)kcc_multi(1, lqProb, varargin{:});
kccOptMeanNVarPVar = @(lqProb, varargin)kcc_multi([1 gamma_pos^2 ; 1 -(gamma_neg^2)], lqProb, varargin{:});

%Solve iteratively
% Init with trajectory in scene without obstacles
[x_init, u_init, L_init, cost_init, eps_init] = ...
    iterativeLQSolver(dynamics_function, costWithoutObstacles, ...
                      ExpectedCost, dt, T, x0, u0, uMin, uMax, ...
                      max_iter, plotWithoutObstacles); 
[x_exp, u_exp, L_exp, cost_exp, eps_exp] = ...
    iterativeLQSolver(dynamics_function, costWithObstacles, ...
                      ExpectedCost, dt, T, x0, u_init, uMin, uMax, ...
                      max_iter, plotWithObstacles);
[x_mvnp, u_mvnp, L_mvnp, cost_mvnp, eps_mvnp] = ...
    iterativeLQSolver(dynamics_function, costWithObstacles, ...
                      kccOptMeanNVarPVar, dt, T, x0, u_exp, uMin, uMax, ...
                      max_iter, plotWithObstacles);

%% Simulate solutions and get statistics
n_sims = 75;
idx_rob = 1;
idx_des = 5;
idx_obs = 9;

% Trajectories and cost stats
[x_trajs_exp, u_trajs_exp, sobs_exp] = ...
    stochastic_n_simulations(n_sims, dt, T, x0, x_exp, u_exp, L_exp, ...
                             dynamics_function, sobs_pos, sobs_Sigma);
[cost_stats_exp] = ...
    compute_cost_stats(costWithObstacles, x_trajs_exp, u_trajs_exp, dt);

[x_trajs_mvnp, u_trajs_mvnp, sobs_mvnp] = ...
    stochastic_n_simulations(n_sims, dt, T, x0, x_mvnp, u_mvnp, L_mvnp, ...
                             dynamics_function, sobs_pos, sobs_Sigma);
[cost_stats_mvnp] = ...
    compute_cost_stats(costWithObstacles, x_trajs_mvnp, u_trajs_mvnp, dt);

% Collision stats
rob_size = 0.05;
[avg_colls_exp, var_colls_exp] = ...
    compute_collisions(x_trajs_exp, idx_obs, rob_size);
[avg_colls_mvnp, var_colls_mvnp] = ...
    compute_collisions(x_trajs_mvnp, idx_obs, rob_size);

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]Jose Medina (2018) Locally optimal risk-sensitive and cost-cumulant control

🌈4 Matlab代码、数据、文章下载