驭码 CodeRider 2.0——数学公式锦集2、初中几何图形公式+函数与统计公式-LaTeX表达式

前言

本系列的一些文章是为了总结一些数学的常用公式，例如初中高中的数学常用公式，物理的公式也不少我也会添加上，完整的测试一下这个驭码对于数学、物理公式的掌握程度，也算是专项测试了，希望能给大家带来一定的价值。

前置驭码 CodeRider 2.0使用链接：驭码CodeRider 2.0 新品体验——情感交流大师(女生版)-优快云博客

通过这篇文章可以对 驭码 CodeRider 2.0做一定的了解，我们再来搞我们的数学会在基础操作上有很多的帮助。

几何图形公式

图形类别	周长 / 面积公式	体积 / 其他公式
三角形	- 面积：S = \frac{1}{2}ah（a为底，h为高） - 勾股定理：a^2 + b^2 = c^2（直角三角形，c为斜边）	- 中位线定理：中位线平行于第三边且等于其一半 - 内角和：180°
矩形	- 周长：C = 2(a + b) - 面积：S = ab	- 对角线相等且互相平分
正方形	- 周长：C = 4a- 面积：S = a^2	- 对角线长：d = a\sqrt{2}
平行四边形	- 周长：C = 2(a + b) - 面积：S = ah（a为底，h为高）	- 对角线互相平分
梯形	- 周长：C = a + b + c + d（四边之和） - 面积：S = \frac{1}{2}(a + b)h（a,b为上下底，h为高）	- 中位线长：\frac{1}{2}(a + b)
圆	- 周长：C = 2\pi r = \pi d - 面积：S = \pi r^2	- 扇形面积：S = \frac{n}{360}\pi r^2（n为圆心角度数） - 弧长：l = \frac{n}{180}\pi r
长方体	- 表面积：S = 2(ab + bc + ac) - 体积：V = abc	- 对角线长：\sqrt{a^2 + b^2 + c^2}
正方体	- 表面积：S = 6a^2 - 体积：V = a^3	- 对角线长：a\sqrt{3}
圆柱体	- 侧面积：S_{\text{侧}} = 2\pi rh - 表面积：S = 2\pi rh + 2\pi r^2 - 体积：V = \pi r^2h	- 展开侧面为矩形，长为底面圆周长
圆锥体	- 侧面积：S_{\text{侧}} = \pi rl（l为母线长） - 体积：V = \frac{1}{3}\pi r^2h	- 母线、底面半径与高满足勾股定理：l^2 = r^2 + h^2

具体测试效果：

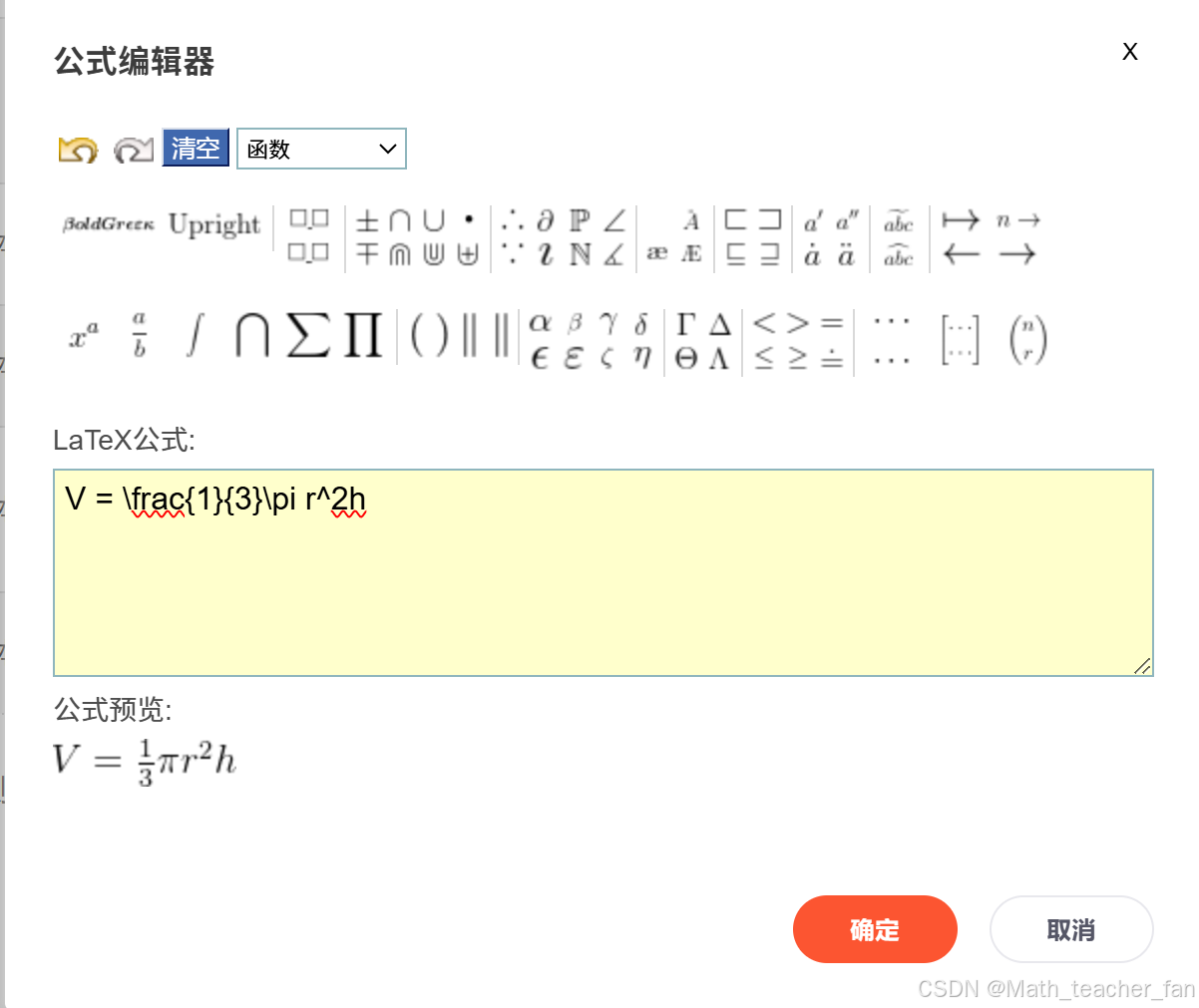
可以看到是没有问题的：

同理我们就可以获取其它的各类公式了：

函数与统计公式

公式类别	公式表达式	说明 / 应用场景
一次函数	一般式：y = kx + b   (k≠0) 斜率：k = \frac{y_2 - y_1}{x_2 - x_1}	k决定直线倾斜程度，b为y轴截距，两点(x_1,y_1),(x_2,y_2)确定直线
反比例函数	y = \frac{k}{x}（k≠0)	图像为双曲线，(k>0)时在一、三象限，(k<0)时在二、四象限
二次函数	一般式：y = ax^2 + bx + c (a≠0) 顶点式：y = a(x - h)^2 + k 顶点坐标：(h,k) = \left(-\frac{b}{2a}, \frac{4ac - b^2}{4a}\right)	图像为抛物线，a决定开口方向，顶点为最值点，对称轴为x = -\frac{b}{2a}
平均数	算术平均数：\bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n}	描述数据集中趋势，需注意极端值影响
方差	s^2 = \frac{1}{n}[(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \dots + (x_n - \bar{x})^2]	衡量数据离散程度，方差越小数据越稳定
标准差	s = \sqrt{\frac{1}{n}[(x_1 - \bar{x})^2 + \dots + (x_n - \bar{x})^2]}	方差的算术平方根，单位与数据一致

其它公式

公式类别	公式表达式	说明 / 应用场景
绝对值性质	\vert a \vert = \begin{cases} a, & a \geq 0 \\ -a, & a < 0 \end{cases}	表示数轴上点到原点的距离，满足\(\vert a \vert \geq 0\)
科学记数法	a \times 10^n (1 \leq \vert a \vert < 10)，n为整数	表示大数或小数，如光速3 \times 10^8 m/s
比例性质	若\frac{a}{b} = \frac{c}{d}，则\(ad = bc\)（交叉相乘） 合比性质：\frac{a + b}{b} = \frac{c + d}{d}	用于解比例方程、相似图形计算
三角函数（直角三角形）	\sin A = \frac{\text{对边}}{\text{斜边}} \cos A = \frac{\text{邻边}}{\text{斜边}} \(\tan A = \frac{\text{对边}}{\text{邻边}}	锐角三角函数值与边的关系，常用于解直角三角形

 总结

都是用驭码 CodeRider 2.0抠出来的LaTeX表达式，挺好用的，特别是让生成例题，自己刷题的视口一定有用。

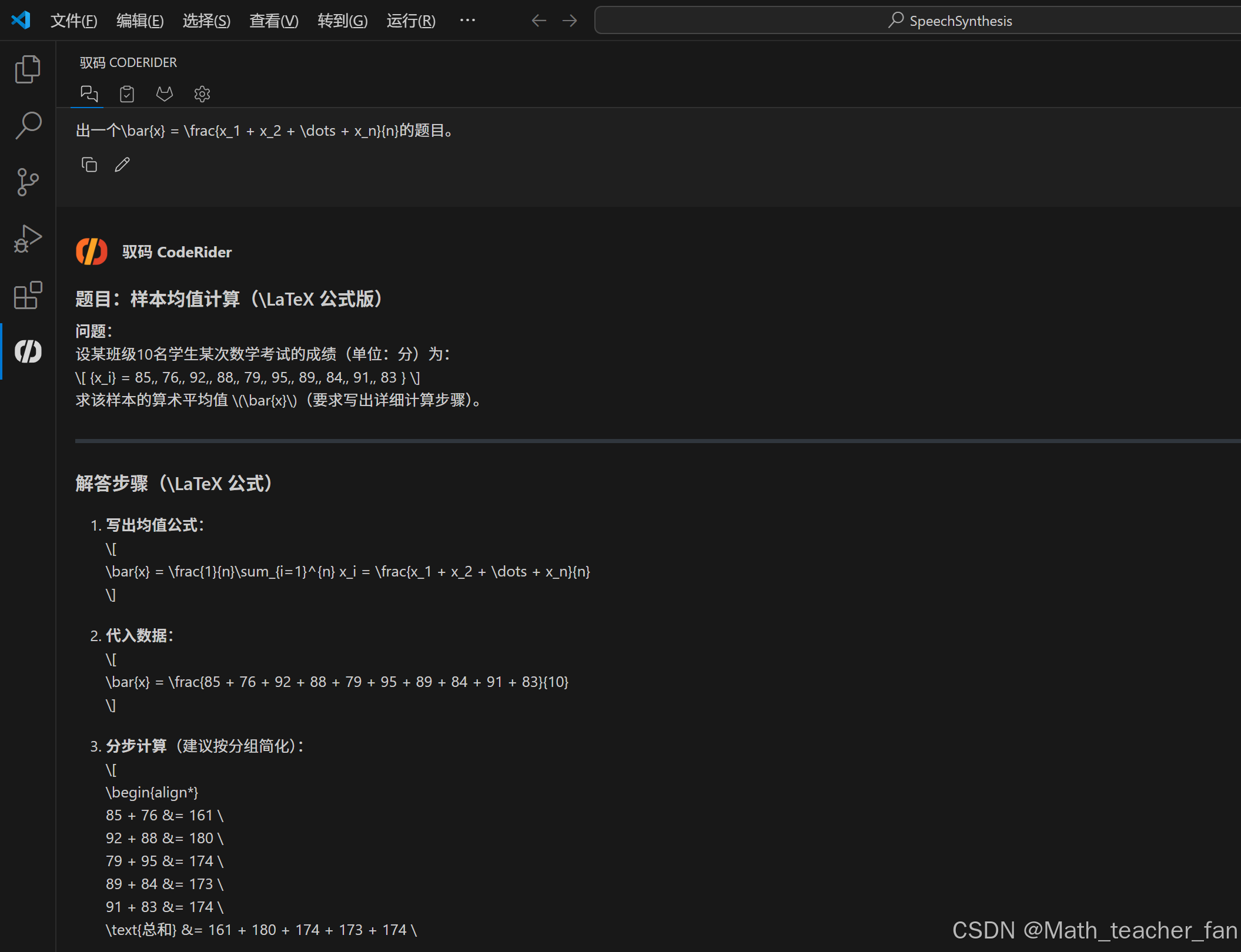
题目：样本均值计算（\LaTeX 公式版）

问题：
设某班级10名学生某次数学考试的成绩（单位：分）为：
\[ {x_i} = 85,, 76,, 92,, 88,, 79,, 95,, 89,, 84,, 91,, 83 } \]
求该样本的算术平均值 \(\bar{x}\)（要求写出详细计算步骤）。

解答步骤（\LaTeX 公式）

1. 写出均值公式：
   \[
   \bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i = \frac{x_1 + x_2 + \dots + x_n}{n}
   \]

2. 代入数据：
   \[
   \bar{x} = \frac{85 + 76 + 92 + 88 + 79 + 95 + 89 + 84 + 91 + 83}{10}
   \]

3. 分步计算（建议按分组简化）：
   \[
   \begin{align*}
   85 + 76 &= 161 \
   92 + 88 &= 180 \
   79 + 95 &= 174 \
   89 + 84 &= 173 \
   91 + 83 &= 174 \
   \text{总和} &= 161 + 180 + 174 + 173 + 174 \
   &= 862
   \end{align*}
   \]

4. 求均值：
   \[
   \bar{x} = \frac{862}{10} = 86.2
   \]

5. 最终结果：
   \[
   \boxed{\bar{x} = 86.2}
   \]